互动科普

本专栏的读者大概都熟知幻方。比如说，取1到16的连续整数，把它们排列成一个4×4的正方形，使每一行、每一列以及两条对角线上的数之和均相等。如果你找到了这样一种排列方法，那么你就做成了一个4阶幻方，而那个共同的总和则称为此幻方的幻常数。如果你能把1到25的整数排成一个5×5的正方形，使之满足上述要求，那么你就作出了一个5阶幻方，如此类推。

幻方是颇受人们喜爱的趣味数学问题，而且这个问题看来总是能够不断地翻新花样。然而，要想对这个问题的基本数学原理作出新的贡献，那就困难得多了。Kathleen Ollerenshaw和David S．Bree1998年发表的一部精彩著作正是作出了这样一种贡献。该书的题目有点令人望而生畏：“最完美的泛对角幻方的结构与数目”(Most—Perfect Pandiagonal Magic Squares：Their Construction and Enumeration，英国滨海绍森德数学及其应用研究所出版。)该书提出了幻方领域中尚未解决的最重大问题之一——统计任一给定阶数的幻方有多少个——的第一个值得注意的部分解答。主要结果是得出了一个计算所谓“最完美幻方”的数目的公式(最完美幻方是幻方的一个特殊子集，具有特别引人注目的性质。)为了不让人们觉得这个问题听起来似乎易如反掌，有必要指出，12阶之类幻方的数目超过220亿，而36阶的数目则约有2．7×1044个之多。显然，你不可能把这些幻方一一写出来以统计它们的数目。

Ollerenshaw和Bree利用数学的一个分支一一组合学——来解决这个问题。组合学研究的是通过捷径来统计某种东西的数目的方法，也就是无需列出这些东西而清点其数目。此项研究的一项值得注意的特点是，两位作者均非专业数学家。现年87岁的Ollerenshaw的职业生涯主要是担任英国若干所大学的高级行政人员，而Bree则先后担任过大学的商业研究、心理学以及最近是人工智能等专业的职位。

出于数学上的考虑，用0，1，2…．，n2-1等整数来建立一个n阶幻方是比较方便的，上面所提到的那本书以及本专栏均采用这一约定。但是传统的幻方中没有零这个数，而是使用1，2，3…，n2等整数。这两种规定没有什么实质性的差别。如果你给数学幻方中每一项均加上1，就得到一个传统幻方；反之，如果你从传统幻方的每一项中减去1，就得到一个数学幻方。这种转换所造成的唯一变化是幻方的幻常数改变了——幻常数将增加n或减少n。

1阶幻方只有1个，就是孤零零的0这个数。2阶幻方是不存在的(这是唯一一个不存在幻方的阶数)，因为幻方的条件要求它的所有4项都必须相等。3阶幻方有8个，但它们全都可以通过对一个幻常数为12的3阶幻方进行旋转或镜面反射变换而得到：

幻方的旋转或镜面反射得到的仍然是幻方，因此所有3阶幻方实际上是同一个东西。然而，4阶幻方就有许多不同的形式了；随着阶数的上升，幻方的数目飞快地增加。目前还不知道幻方阶数与幻方个数之间关系的精确公式。

取得进展的途径之一是对幻方规定更多的条件。出于本文的需要，最自然的这种条件是幻方应当是“泛对角”的(pandiagonal)——也就是说幻方所有的“断开对角线”(broken diagonal)上的数字之和必须也等于幻常数(所谓断开对角线，就是从幻方的一条边出发绕一圈到达对边的一条线。)泛对角线幻方之一例是下面这个幻常数为30的幻方：

在这个幻方中，断开对角线的例子有11+8+4+7和11+14+4+1等，两条对角线上的数字各自加起来均等于30。3阶幻方不是泛对角的，例如，8+2+5等于15而不是12。事实上，仅当一个幻方的阶数为二重偶数时——也就是为4的倍数时——它才可能是泛对角的。

最完美幻方所受到的限制还要多。除了必须是泛对角的幻方以外，它们还必须具备这样一条性质由相邻项组成的任意一个2×2子矩阵的所有各项之和相等，即都等于2n2-2，其中n为幻方的阶数。(也可以证明，任何具有这种2×2子矩阵性质的幻方必定是泛对角的。)上面所示的4阶幻方是最完美的一一例如，由0，11，14和5等项组成的一个2×2子矩阵的各项之和等于30。

注意，从幻方的一边出发绕一圈到另一边构成的2×2子矩阵也包括在内，例如由3，4，14和9构成的子矩阵。图1所示的12阶幻方是最完美幻方的一个更有气派的例子。

Ollerenshaw和Bree的计数方法的关键在于最完美幻方与“可逆正方形”(reversible square)之间的联系。为了弄清这些问题，我们需要解释若干术语。把一个整数序列倒转过来并把对应的数分别相加，如果得出的和全部相等，我们就说这个整数序列具有反转相似性(reverse Similarity)。例如，序列1，4，2，7，5，8具有反转相似性，因为把它反转过来后得到8，5，7，2，4，1这个序列，两个序列对应项相加分别为1+8，4+5，2+7，7+2，5+4，8+1，这些和全部等于9。

n阶可逆正方形是由0，1，2，．．．，n2-1等整数构成的一个n×n阵列，它具有下列性质：它的每一行与每一列均具有反转相似性，而且在该正方形内的任何一个矩形阵列中，对角的项分别相加后其和相等。例如，从0到15的整数按递增顺序构成的4×4阵列为可逆正方形，如下图所示。举例来说，在第三行中，8+11=9+10=19。同样的规律对其它所有各行及所有各列均成立。此外，这个正方形也满足第二个条件，如5+11=7+9和1+15=3+13：

可逆正方形通常不是幻方，但Ollerenshaw和Bree证明，每一个二重偶数阶的可逆正方形均可以通过一种特殊的方法转变成最完美的幻方，而每一个最完美的幻方均可以通过这种方式作出来。现在我们以上面这个4阶可逆正方形为例来说明这种方法。首先，把每一行的右半部分反转过来：

接着将每一列的下半部分反转：

现在把正方形分成2×2的子矩阵。将每个子矩阵中的4项按下面所示的方式移动：

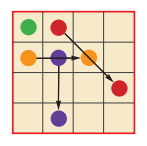
也就是说，左上角的一项不动，右上角一项沿对角线方向移动两个方格，左下角的一项向右边移动两个方格，而右下角的一项向下移动两个方格。如果某一项象这样移动后跑到4×4正方形的外面去了，那么就把正方形卷起来使其对边相连而找出该项的移动后位置。(这一特殊的方法仅适用丁4阶正方形。对于n阶正方形这一特殊情形，有一种用数学公式表示的类似方法。)对于本例，最后结果就是下面这个最完美的幻方：

这种转换过程建立了最完美幻方和二重偶数阶可逆正方形之问的一个一一对应关系。因此，为了统计某一阶的最完美幻方的总数，你可以统计相同阶数的可逆正方形的总数。乍看起来，把问题的性质象这样变一下似乎不能解决多大问题，但结果证明可逆正方形有n个十分巧妙的特点，使我们可以统计这类正方形的数目。

特别是，可逆正方形可以分为若干类。每一类中的所有可逆正方形都可以通过各种变换(例如旋转、镜面反射和其它几种更复杂的变换)互相联系起来。为了构造出属于某一类的所有可逆正方形，只要构造出其中一个并照常规应用这些变换就行了。此外，每一类都有恰好一个“主”正方形。最后，每一类的大小都是相同的。每一类中有实质性差异的正方形的数目为2n-2((n／2)!)2，其中惊叹号表示阶乘。(例如，6!=6×5×4×3×2×1=720。)

因此，只要统计一下任一阶数的主可逆正方形有多少个，然后把此数目乘以上述式子就行了。这样得到的结果就是上述阶数的有实质性区别的最完美幻方之数目。主可逆正方形的数目本身也可以用一个公式计算，但这个公式较为复杂。发现并证明这个公式需要用到更深的组合学知识，因此我不准备详述这个问题了，只是指出对于n=4，8，12和16这几个二重偶数阶来说，不同的最完美幻方的数目分别为48，368640，2.22953×1010和9.322433×1014。