互动科普

描述海岸线形状和星系模式的几何学也可以解释股票价格如何疯涨与暴跌。

个体投资者与专业股票和货币炒家比任何时候都更清楚地知道，任何金融市场上的股票牌价变化之快常常令人心跳骤停。当市场的变化似乎突然加速，行情越来越反复无常时，投机者转瞬之间就可以赚到大笔钱或亏掉大笔钱。例如，1998年9月，法国的通信设备制造商Alcatel公司的股票价格一天就下跌了40％随后几天又下跌了。然后，第四天，该公司的股票走势又逆转，股价上升了10％。

本世纪大部分时间使用的经典金融模型预测，这样的急升急降事件是永远也不应当发生的。金融学的基础之一是现代证券理论。该理论的目标是，对于给定水平的风险，取得尽可能大的收益支撑这种证券理论的数学在处理极端情况时，作了尽可能从宽的忽略：它认为重大的市场剧变出现的可能性太小，以致没有什么重要性，或者认为这类变化无法加以考虑。不错证券理论或许能解释市场在95％的时间里发生的情况。然而，如果人们承认重大的事件就包含在剩下的5％内的话，那么这个理论所描述的图景就没有反映实际情况。人们必然会想到用海上航行的水手来作一个比喻：如果大海在95％的时间里风平浪静，水手是否能对发生台风的可能性视而不见？

证券理论提出的防范风险的措施依靠的是一些要求很严的、而且终究没有什么根据的假设。首先，它认为价格的变动统计上是彼此独立的：例如，今天的价格对于现行价格和明天的价格之间的变化毫无影响因而，预测未来的市场动向就成了不可能的事情。第二个假设是，所有的价格变化的分布服从标准钟形曲线，这一模式钟形的宽度(用它的σ值即所谓标准差来量度)描述了价格变化偏离平均值有多远极端情况的事件被认为是极其罕见的。事实上这一理论规定台风是不存在的。

金融资料是否与这些假设完全相符？当然从来不是如此。股票或货币随着时间变动的走势图的确显示了一个价格小幅上下波动的恒定背景——但这些变化并不象人们根据价格变动符合钟形曲线这一假设所预期的那样均匀。不过，这些变化趋势仅是走势图的一个方面，还有相当多的突然的剧烈变化——在走势图上呈现为急升急降的尖峰如象Alcatel公司的股票那样——在较为平缓的变化的背景上显得十分突出。而且，价格变动的幅度(无论大小)可能在一年的时间里保持大致恒定然后在一段很长的时间里其变化程度又突然加剧。在市场的混乱加剧时，价格的急升急降就变得越来越常见，在走势图上呈现为密集分布的形态。

根据证券理论，这些大的价格波动的概率为亿亿亿分之几(波动大于10个标准偏差)。事实上，人们经常观察到尖峰——频繁到每个月都会出现——而它们的概率高达百分之几。诚然，钟形曲线常常被说成是“正常”的(或者更确切地说是正态分布)。但金融市场难道就应该被认为是不正常的吗？当然不应该——金融市场是客观实际，有问题的是证券理论。

现代证券理论对于那些过分相信它的人来说是危险的，而对于理论家来说则是一个强有力的挑战。虽然该理论的信奉者们有时也承认现行的思考方式存在问题，但他们认为其它任何假设都无法通过数学模型来加以处理。这一争论产生了这样一个问题：是否可以研究出一种至少能解释重大金融震荡的若干特征的严格的定量描述？对于这个问题，悲观的的回答是，重大的市场剧变是异常现象，是各种不具有任何规律性的“不可抗力”。改良者对现代证券理论的这些大成问题的假设作了若干小修小补，但这些修修补补缺乏指导原则，因此并没有使它们获得足够的改进。我自己多年的研究工作所持的，是一种完全不同的、而且肯定是乐观的立场。

我认为，金融市场价格的变动，可以用根据我在分形几何中的研究成果推导出的一个模型加以解释。分形——经过进一步发展后称为多分形——的目的并不是要确切地预测未来。但是它们的确是对市场风险的更切合实际的描述。鉴于一些大的投资共同基金——称为保值基金(hedge funds)——最近陷入了困境，拒绝研究对风险作出更准确估计的模型是很不明智的。

多分形与市场

分形利多分形的研究已经存在着一个很广泛的数学基础，分形模式不仅出现在证券的价格变动中，而且出现在整个宇宙星系的分布中、海岸线的形状中以及无数的计算机程序生成的装饰图案中。

分形是一种几何形状，其特点是可以分为若干部分，而每一部分都是最初那个整体在较小尺度上的翻版。在金融学中，这一概念并不是无根据的抽象，而是对一种简单明了的市场常识——也就是把市场走势图放大或缩小，以使其符合同一时间和价格尺度时一种股票或货币的变动情况看起来全都相似——从理论的高度上重新进行表述。由于分形的这一性质，观察者无法确定哪些数据涉及的是从一周到下一周的变化情况，哪些数据是从一天到下一天的变化情况，等等。这一性质把这些走势图划在了分形曲线的范畴内，从而使人们可以利用许多强有力的数学和计算机分析工具来研究它们。

描述部分和整体之间的这种相似性的一个更具体的专门术语是“自类同”（self-affinity）。此性质与人们更熟悉的一个分形概念——即自相似（self-similarity）有关。所谓自相似，就是某一图形的每个特征都按同一比例缩小或放大，任何一个到相片洗印店放大过相片的人都很熟悉。然而金融市场的走势图远远不是自相似的。

在一幅其各个特征的高度大于宽度——例如股票走势曲线中价格的每一次升降变化——的图形细节中从整体转换到部分必定会使水平轴缩短得比垂直轴更多。对于价格走势图这一转换必定使时间尺度(水平轴)比价格尺度(垂直轴)缩短得更多。整体相对于其各部分的，这种几何关系就被称为是自类同的关系。

大多数统计学家对于不变性质的存在并不甚重视，但是物理学家以及象我这样的数学家则十分喜爱此类性质我们称其为“不变性”(invariance)：对于呈现出引人注目的不变性质的模型，我们总是爱不释手，我所说的意思可通过一个很好的方法来加以阐明，就是画一幅走势图，并逐步地在图上表示出从时刻零到随后的某一时刻(时刻1)之间的价格变化。时间间隔本身是随意选择的，可以是1秒，也可以是1小时1天或1年。

此过程的第一步是用l条直的走势线来表示某一价格(见图1)。然后用1条称为生成元(generator)的折线来产生对应于金融市场的牌价上下波动情况的图形，生成元由3段组成沿着直的价格走势线插入即内插(如果使用少于3段的生成元则不能模拟可以上下变动的价格)。在画出了初始生成元之后，它的3段再分别用3个较短的生成元来内插重复这些过程，就在缩小了的尺度上重新得出生成元(或价格曲线)的形状。水平轴(时间尺度)和竖直轴(价格尺度)都被压缩了，以便同生成元每一段的水平边界和竖直边界相配合。

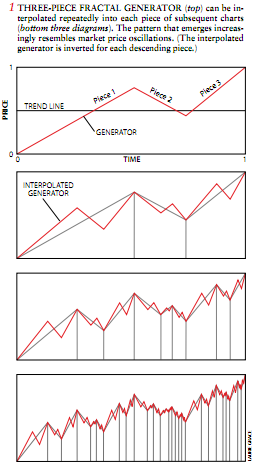
无休止的内插

图1只示出了用生成元进行内插的最初几步，但这同一过程可以持续不断地进行下去。从理论上说它是没有终结的。不过在实际上，内插进行到比炒股交易的间隔时间(可能短于1分钟)还短的时间上就没有什么意思了。很显然，每一段最终的形状都与整体的形状大致相似也就是说，尺度不变性之所存在，纯粹就是因为它在画图过程中已被塞了进去。新颖之处(也是出人意料之处)在于，这些自类同的分形曲线展示出十分丰富的结构，而这是分形几何学与混沌理论的基础之一。

若干精选的生成产生出所渭的单分形曲线，它们所展示的正是现代证券理论所容纳的相对平稳的市场图景。但是只有在这些特殊的生成元才能予以满足的某些极不寻常的特殊条件下、平稳性才会占优势。这种过分简化的模型所依据的假设是现代证券理论的最大失误之一。此理论很有点象某个关于海洋波浪的理论不允许浪涛高度超过6英尺。

分形几何的精美之处在于，借助这种几何研究人员能够构造出一种普遍适用的模型。它不但能复现证券理论描述的平稳市场所特有的模式，而且能复现最近几个月中剧烈振荡的金融交易状况。刚才介绍的那个建立分形价格模型的方法，经修改后可显示市场活动是如何加速及放慢的，即显示市场易变性的实质。这一易变性是“分形”这个术语的前面要加上字头“多”的原因。

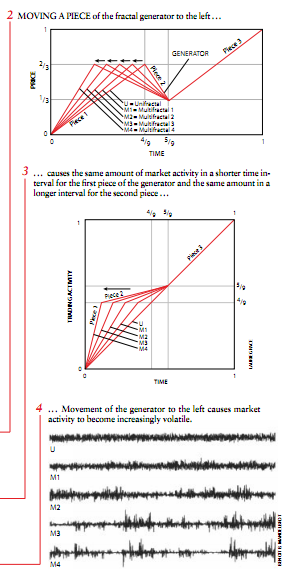
为了从单分形创造出多分形，关键的一步是拉长或缩短水平时间轴，使生成元的各段或者被拉伸，或者被压缩，与此同时垂直价格轴可以保持不变。在图2中，单分形生成元的第1段被逐步缩短，这样也就有了地方来拉长第2段。在作了这些调整以后生成元就变成多分形了(M1到M4)。在这个生成元的第1段所代表的时间区间中市场活动的速度加快，而在对应于第2段的时间区间中，市场活动的速度放慢(见图3)。

利用前面介绍的内插过程，对生成元进行的这样一种改动能够产生对某一给定时间内价格变动的完整模拟。每当生成元的第1段被进一步缩短时以及逐次内插过程完成以后，它所产生的图形就越来越象易变市场的特征了(见图4)。

此处所示的单分形(U)的图(在被缩短之前)对应于证券理论家们的模型中所假定的较平稳的市场。从M1向下到M4每一走势图同该模型的差距越来越大，显示出急剧的、尖峰状的价格变动以及同不久前的市场交易相类似的持续大幅度的波动。为了使关于易变市场的这些模型具有必要的现实性，每一生成元的3段是打乱了的，但这一过程在上述图中没有表示出来。此过程的操作方法如下：想象有这样一颗骰子，它的每一面是生成元各段的6种组合方式中某一种的组合方式的图象。在进行每次内插之前，先要掷这颗骰子然后选择骰子朝上的一面所代表的组合方式进行内插。

企业的财务主管、现汇炒卖者或其他市场谋略家从这些分析中应当得出什么样的结论呢？现代证券理论所描绘的情景以及实际的价格变动之间的差异是很明显的，价格并不是连续变化的，它们在所有时间尺度上无规律地起伏易变性——它远非一种可以忽略不顾或轻易补偿的静态文体——正是金融市场上所发生的过程的核心。过去财务主管们认同现代证券理论的连续性以及受约束的价格变动等观点，因为没有什么更好的理论来替代它。但是现在财务主管再也不必按其表面价值来接受当前的金融模型了。

现在人们可以利用多分形来对证券进行“应力测试”。这种方法是利用支配多分形的规则来产生支配真实市场的未知规则所产生的那些变化模式，多分形精确地描述了生成元的形状以及实际市场资料图表上待发现的价格上下波动规律之间的关系。

从实用角度看，这一发现提示，分形生成元可以根据市场的历史资料结出来所用的实际模型并不仅仅考察市场昨天或上个星期发生的情况事实，它是市场波动的更现实的描述，称为多分形交易时间中的分数布朗运动。这个模型产生的生成元所创造的图形可以模拟以先前的市场活动为基础的替代变化图景。

这些方法并不会使人们能够更有把握地根据过去的资料预测某一天的股价是升还是降，但是它们提供了关于市场动向的概率的估计值，据此人们可以对必将发生的重大变化作好准备。新的模拟方法向金融市场似乎是无法预测的一团混沌中注入了某些有序性，它们也对水手的下述告诫一一即使是在风平浪静的海上，一场暴风也可能就在地平线上悄然逼近一一给予了高度重视最近的事件表明，这一告诫是值得注意的。 

【戴平／译 冉隆华／校】