互动科普

如果能建造出来的话，量子力学计算机将能完成任何常规计算机无力完成的工作。

过去50年中，计算机的速度每两年一番，而其元件的尺寸则每两年缩小一倍。电路中包含的导线和晶体管的宽度现在仅有人的头发丝的百分之一。由于这一爆炸性的进展，现今的计算机的功能比其雏形提高了数百万倍、但是爆炸最终会消散，而集成电路技术观在正在逼近其极限。

高级光刻技术可以生产出比现有元件小一百倍的元件。但是在这一尺度上，一块物质呈现为单个原子的集合，而集成电路仅勉强能工作。再小10倍，单个原子便表现出自己的个性，而一个缺陷就能造成大破坏。因此，如果计算机在将来要进一步大大变小，就必须用新技术来补充或取代现有的技术。

几十年前，一些先驱者——如IBM 公司Thomas J. Watson 研究中心的Rolf Landauer和Charles H. Bennett——便开始研究信息处理电路的物理性质，提出了关于微型化可能发展到何种地步的若干问题：电路元件能够做成多小？再计算的过程中必须使用多少能量？由于计算机是物理器件，因此它们的基本工作过程可用物理学描述。一个严峻的物理事实是，当计算机元件的尺寸变得非常之小时，必须用量子力学来对它们进行描述。

八十年代初，阿贡国家实验室的Paul Benioff根据Landauer和Bennett的早期成果，证明了一台计算机原则上可以纯粹量子力学的方式运行。此后不久，牛津大学数学研究所的David Deutsch和美国及以色列的其它科学家开始对量子力学计算机进行模拟，以弄清它们与经典计算机有什么区别。特别是，他们想知道是否可以利用量子力学效应来加快计算速度或以新颖的方式进行计算。

到八十年代中期，这一研究领域由于若干原因而衰落了。首先，所有这些研究人员都是从抽象的角度来考虑量子计算机，而不是研究实际的物理系统——Landauer已列举了这一方法的许多缺点。此外，还有一点也逐渐变得明显：量子力学计算机可能易出错误，而且不容易纠正错误。除了由加州理工学院已故的 Richard P. Feynman 提出的一项建议外——他提出量子计算机可用于模拟其它的量子系统，例如新的或未观察过的物质形式——尚不清楚量子计算机解决数学问题是否会比常规计算机快。

在过去3年中，这一情况已发生了变化。1993年，我描述了一大类人们熟悉的物理系统，这些物理系统的行为可能类似于量子计算机，而在某些方面避开了 Landauer所指出的问题：美国电报电话公司贝尔实验室的 Peter W. Shor证明了量子计算机可明于分解大数——分解大数的任务可以使功能最强大的常规计算机也一筹莫展。过去一年中，在意大利都灵科学交流中心举行的讨论会提出了许多建造量子电路的设计。最近，加州理工学院由H. Jeff Kimble领导的研究小组和国立标准与技术研究所由David J. Wineland领导的研究小组建造了某些原型部件。本文将解释量子计算机是如何组装的，并介绍若干量子计算机能完成而数字计算机不能完成的非凡的任务。

量子力学

我们必须正视这一现实：量子力学是十分奇妙的。曾协助开创量子力学的丹麦物理学家尼尔斯•玻尔曾说：“任何能思考量子力学而又没有被搞得头晕目眩的人都没有真正理解量子力学。”无论如何，量子力学预测了一系列违反常识的效应，而它们已被实验一次又一次地证实、要了解量子力学的奇异本领，我们只需接受—个称为波粒二象性的事实。

波粒二象性意味着我们平常认为是固体粒子的事物（如篮球和原子），在某些情况下其性质类似于波，而我们平常描述为波的事物（例如声音和光），有时却表现出粒子的行为。实际上，量子力学的理论规定了哪些类型的波与哪些类型的粒子相关，反之亦然。

波粒二象性的第一个奇异的影响就是微小系统（如原子）只能以分立的能态存在。这样，当原子从一个能态变到另一个能态时，它就吸收或放出精确数额的能量，称为光子。光子可看作是构成光波的粒子。

第二个后果则是量子力学的波如同水波一样可以叠加。即加在一起。分开来看，这些波都是对某个粒子的位置的粗略描述。但是，当两个或两个以上的这类波叠加起来时，粒子的位置就不清楚了。这样，在某种奇异的量子意义上，一个电子有时候可以同时既在这里又在那里。这样一个电子的位置只有到某种相互作用(例如一个光子从该电子上散射）暴露了它是在这里或是在那里（但不是同时在两处）时才能为人们所得知。

当两个互相叠加的量子波其行为就像一个波那样时，这两个波称为相干的。两个相千波重新恢复其各自身份的过程称为去相干(decoherence)。对于—处于两种不同能态的叠加态中的电子（或者概括地说，就是在原子内处于两种不同位置的叠加态中的电子），去相干可能需要很长的时间。比如说，可能要过几天后才会有一个光子撞上一个像电子那么小的物体，从而暴露电子的真实位置。原则上，篮球也可以同时既在这里飞在那里（即使迈克尔•乔丹不出场）。但在实际上，一个光子从篮球上散射所需的时间太短，以致眼睛和任何仪器都无法检测出来。篮球太大了，因此它的精确位置不可能在任何一段可察觉的时间中不被人们所注意。因此，一般只有微小的事物显示出量子力学的奇特性质。

量子信息

信息同量子力学中的原子能级一样也是呈分立的形式。信息的量子就是位。一位信息就是两种可能情况中的一种——否或是，0或1,假或真。在数字计算机中，电容器板之间的电压表示一位信息：带电的电容器表示1,而放电了的电容器表示0。量子力学计算机就是通过使数字信息处理的人们熟知的分立特性与量子力学的奇异的分立特性相对应而进行计算的。

事实上，一串氢原子可以像一串电容器一样存储信息位。其电子处于基态的原子可以代表0,而电子处于某一激发态的原子则代表1。但是，要使任何这样一种量子系统像计算机那样运行，它除了存储信息外还必须具备其它的能力。操作人员必须能把信息装入系统，通过简单的逻辑运算处理这一信息；然后把信息卸出。这就是说，量子系统必须能够读出、写入并进行算术运算。

IsidorIssacRabi(1944年获诺贝尔物理学奖）首先说明了如何向量子系统写入信息。他的方法在用于氢原子时是这样进行的。想象有一个处于基态的氢原子，其能量等于E0。要向这个原子写入一个0,实际上就是不采取任何行动。要向这个原子写入1,就把它激发到某一较高能级上（称为E1）。为此，可以用一束激光照射此原子，此激光的光子的能量等于E1与E0之差。如果激光的强度合适,且照射一段适当的时间，则该原子在电子吸收了一个光子后将从基态逐步变到激发态。如果这个原子已经处于激发态，则同一束激光脉冲可使此原子发射出一个光子，并回到基态。用信息存储的术语来说就是脉冲让原子的信息位翻转。

上面所说的“逐步”是什么意思呢？ 一个振荡电场（如激光）推动原子中的电子从一个较低的能态变到一个较高的能态，其方式很像一位家长推着坐在秋千上的孩子越荡越高。每当振荡的波完成一个周期时，它就给电子一点推动。当电场中光子的能量与E0和E1的能量差相等时，这些推动力就与电子的“摆动”运动相重合，并逐步把与电子相对应的波转变成具有不同能量的波的叠加。与电子的基态相联系的波的振幅将随着与受激态相联系的波的振幅的增大而连续地减小。在这一过程中，这个原子存储的信息位从基态“翻转”到激发态。当光子的频率不对头时，它们的推动力将不与电子的运动同步，因此什么也不会发生。

如果光的频率对头，但照射的时间只是使原子从0翻转到1所需时间的一半，则原子所处的状态将等于与1对应的波和与0对应的波叠加，每个波具有相同的振幅。这样一种量子位(qubit)只翻转了一半。相反，经典的信息位读出时不是0就是1。在常规的计算机中，半充电的电容器将造成错误，但在量子计算机中半翻转的量子位则开辟了新型计算的途径。

从量子系统中读出信息位与使它们翻转相类似。把原子激发到一个更高的、更不稳定的能态，称为E2。为 此，用一束其能量与E1和E2之能量差相等的激光照射此原子：如果该原子处于E1态，则它将被激发到E2态，但又迅速返回到E1态，同时放出一个光子。如果该原子已经处于基态，则不会发生任何情况。如果该原子处于“半翻转”状态，则它有同等的机会发射出一个光子（从而表明它是 1)或不发射一个光子（从而表明它是0)。从量子系统的信息读出和写入到计算之间只相隔很小一步。

量子计算

电子电路是由线性元件（例如导线、电阻器和电容器）和非线性元件 (例如二极管和晶体管）构成的。非线性元件的作用是以种种不同方式操作信息位。线性元件独立地改变输入信号，而非线性元件则使经过它们的输入信号发生相互作用。例如，如果你的立体声音响没有非线性晶体管，则你就不能调节它放出的音乐中的低音。为实现这一调节，需要你的激光唱盘上的信息和来自立体声音响调节旋钮的信息作某些协调。

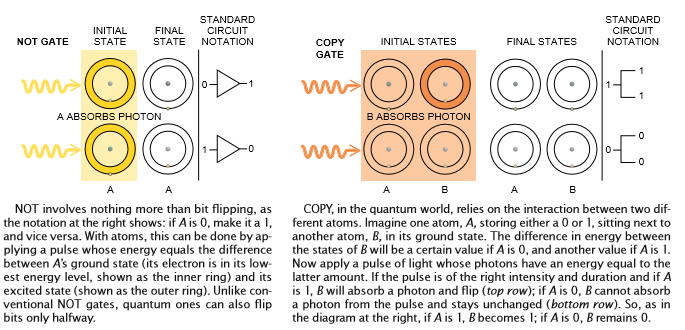
电路通过以极高速度反复完成若干简单的线性和非线性任务来进行计算。一个这样的任务就是使信息位翻转，这相当于所谓“非”（NOT) 的逻辑操作：真变为假而假变为真。 另一个任务是“复制"（COPY),也就是使第二个数据位的值与第一个相同。这两个操作都被称为线性操作。 因为在这两种情况中输出都反映了单一输入的值。对两个数据位作“与” (AND)运算——这是另一个有用的任务——则是一种非线性的逻辑操作:如果两个输入位均为1,则使第三个位也等于1,其它任何一种情况均使第三个位等于0。在这种情况下，输出取决于输入之间的某种相互作用。

执行这些操作的器件称为逻辑门。如果一台数字计算机有线性逻辑门，如NOT门和COPY门，也有非线性逻辑门，如AND门，则它可以完成任何一种逻辑或算术任务。对于量子计算机，同样的要求也是成立的。Artur Ekert 与 Deutsch 和牛津大学的Adriano Barenco证明了量子位之间的几乎任何一种非线性相互作用都能胜任。事实上，只要一台 量子计算机能够翻转数据位，则任何非线性的量子相互作用都使它能执行任何计算。因此，可以利用一大类物理现象来建造量子计算机。

事实上，通用量子逻辑门存在的时间几乎和晶体管一样久！在五十年代后期，研究人员利用粒子的自旋，成功地进行了简单的两位量子逻辑运算。这些自旋——实际上就是粒子相对于某个磁场的旋转方向——同能级一样是量子化的。因此可以用沿一个方向的自旋表示1，而用另一个方向上的自旋表示0。研究人员利用了氢原子中的电子自旋和质子自旋的相互作用；他们建立了一个系统, 在这个系统中，只有当电子的自旋表示1时，他们才能使质子的自旋翻转。由于这些研究人员当时并没有考虑量子逻辑的问题，因此他们称此效应为双重共振。然而他们使用双重共振进行了线性的NOT和COPY操作。

自那时以来，Barenco, IBM公司的David Divincenzo,纽约大学的Tycho Sleator和因斯布鲁克大学的 Harald Weinfurter 已证明，通过质子和电子的自旋部分地翻转，也可用双重共振来建造一个AND门。把这些量子逻辑门通过导线连在一起，就可以做成一台量子计算机。不用说，量子“导线”是很难制造的。在常规计算机中，导线只需用很容易把电压信号从一个逻辑门传送到另一个逻辑门的金属条做成。而把双重共振门连接在一起是一项极为困难的任务：此时导线必须能够把原子拆开以便任意地运送电子和质子，而后又必须能把原子组合起来，所有这些操作都不能干扰粒子的自旋。

研究人员最近设想出了比较简单的办法来连接量子逻辑门。例如, 穿过光纤或空气的单个光子能够把信息位从一个逻辑门运送到另一个逻辑门。一项特别有希望的成就来自加州理工学院：Kimble的研究小组通过把光子连同一个原子集中在一个微小区域中而增强了光子之间的通常是很微弱的非线性相互作用。其结果是得到一个量子逻辑门：当另一个光子读出为1时，一个光子位可以部分翻转。完全用这类量子光学门建造的一台计算机的运算速度将非常快，而且相对来说不易受环境扰动的影响(这种扰动可能破坏相干性）。但它仍然面临Landauer所预言的一系列障碍。特別是，这一系统中所有光路的长度都必须精确到所使用的光的波长的一个极小分数的范围之内。

布线问题还有其它方法来解决。西班牙卡斯蒂利亚-拉曼査大学的J.Ignacio Cirac和因斯布鲁克大学的Peter Zoller,提出了一种把量子位封在一个离子阱中的设计方案，实际上使它们与任何有害的外部影响隔绝开来。在对一位进行处理前，它将被送到一个公用寄存器即“总线”中。具体地说，它含有的信息将用一个涉及到离子阱中所有离子的摇摆运动来表示。美国国立标准与技术研究所的Wineland研究小组在实现这样一种量子计算机的道路上已迈出了第一步，对用离子和摇摆运动编码的信息位进行了线性的和非线性的操作。建造有几十位或比百位的离子阱计算机的前景很不错的：两位的操作已经实现，而计算机中的位的数目可以通过向离子阱中加入更多的离子来增大。

按照现状来看，科学家能够控制几个位的量子逻辑运算，在不远的将来，他们很可能用几十位或几百位来进行量子计算。传统计算机通常要处理几十亿位。因此，这怎么可能是对传统计算机的改进呢？事实上,即使只用—位，量子计算机也能做任何传统计算机都做不到的事情。考虑下列情况。取一个处于0和1的叠加态中的原子，现在通过使其发荧光来确定这一位究竟是1还是0。在一半的时间中，该原子射出一个光予，因此这一位是1。在另一半时间中，没有光子射出来，因此这一位是0。这就是说，这一位是随机位，而任何传统计算机都无法做出一个随机位来。数字计算机中的随机数生成程序实际上产生的伪随机数，它使用了一个其输出极不规则的函数，以致看起来它似乎是在随机地产生数位。

多粒量子状态

想象一下量子计算机用两位能够做些什么事情。复制是通过把两个位——其中一个带有待复制的值而另一个的初始值为0——放在一起来进行的。只有当第一位也为1时，用光脉冲来照射才会使第二位也翻转为1。但是，如果第一位的值是0和 1的叠加，则用光脉冲来照射将会产生涉及两个位的一种叠加态，以致两个都是1或两个都是0。注意，第一位的最终值不再与它的初始值相同——叠加态已经改变了。

在这一叠加态的每一分量中，第二位都与第一位相同，但没有一个与其初始的位相同。爱因斯坦指出，这样的状态将会违背关于因果关系的所有经典直觉。在这样一个叠加态中，没有一位处于确定的状态，但是如果你测量一位，从而使其进入一个确定的状态，则另一位也进入一个确定的状态。第一位的变化并不引起第二位的变化，但是由于破坏了这两者间的相干性，测量第一位也就使第二位失去了其不确定性。三个量子位之间能够建立起更奇异的缠结状态。

事实上，只要有两个或三个量子位，再加上一个或两个量子逻辑门，就可以创造出引人入胜的量子状 态。我已经证明，有了更多的位，就可以用量子计算机模拟任何一个量子系统的行为。只要正确地编程，该计算机的动力学特性就会变得与某个假设系统的动力学特性完全相同（包括该系统与环境的相互作用）。此外，这台计算机为绘出此系统随时间的演变情况而需要的步骤的数目也直接与系统的规模成正比。

更值得注意的是,如果一台量子计算机具有并行结构——并行结构可以通过一个晶体的原子中相邻的成对自旋之间的双重共振来实现——则它就能够实时模拟任何一个量子系统，不论其尺寸有多大。这样一类并行量子计算如果能实现，则其速度将大大快于常规方法的速度。正如Feynman所指出的那样，在经典计算机上模拟量子系统，它所需要的步骤数目通常随系统尺寸的增大和跟踪系统行为所用的时间量的增加而呈指数式增长。事实上，一台四十位的量子计算机可以用几乎不多于一百步的步骤就复现出一个量子系统，而这样一个系统需要一台有一万亿位的经典计算机花若干年时间来模拟。

  当对许多量子位进行许多逻辑操作时，一台量子计算机能够做些什么呢？开始时把所有输入位置于0和1的同等叠加态种，每一位具有相同的幅度。这样计算机就处于所有可能的输入的同等叠加态种，现在让这一输入通过一个进行某一特定计算的逻辑电路。其结果将是该计算的所有可能输出的叠加态。在某种奇异的量子意义上，此计算机是在同时进行所有可能的计算。Deutsch称这一效应为“量子并行”。

  量子并行看起来似乎很古怪，不过我们考虑一下波一般是如何起作用的就不难理解了。如果量子力学波是声波，那么对应于0和1的波——分别以单一频率震荡——就是纯音，而对应于0和1的某一叠加态的波就是合唱了。正如音乐上的合唱听起来与它所包含的各种音调有质的区别一样，0和1的叠加态也不同于单独的0和1：在这两种情况下，复合的波彼此相互干涉。

  执行常规计算工作的量子计算机——此时没有位发生叠加——产生出的一系列波类似于英国教堂钟楼发出的“钟调大合奏”的声音，在这一大合奏中，各个钟从不同时敲响，而且其声音的顺序遵循严格的数学规则。以量子并行模式完成的计算类似于交响乐：它的“声音”是许多互相干涉的波的声音。

  贝尔实验室的Shor最近证明，量子并行的交响乐效应或许可用于迅速分解大数——这是一项经典计算机乃至超级计算机都始终不能完成的任务。Shor证明,量子并行计算可加以适当协调，使潜在因子从叠加态中显露出来，正如在中提琴、大提琴和小提琴上奏出的一个高 (或低）八度的旋律将会从交响乐队 中周围乐器奏出的音乐中突出出来一样。事实上，如果能建成一台量子计算机，则他的算法将使分解因数成为量子计算机轻而易举就能完成的一项任务。由于大多数公开钥密码系统——例如保护电子银行帐户的那些密码系统——都有赖于经典计算机不能发现比如说大于100位的因子这一事实，因此量子计算机黑客将使许多人有理由感到焦虑。

量子计算机（以及量子黑客）是否会出现是一个激烈争论的问题。应当记住，只有在环境不以某种方式透露系统的状态时，一个叠加态的量子特性才能占上风。由于量子计算机可能仍由数千个乃至数百万个原子构成，而只要其中一个受到扰动便会破坏量子相干性，因此尚不清楚相互作用的量子系统在真正的量子叠加态中能持续多长时间。实验证据表明，某些系统能使量子叠加态保持几个小时。Shor和他的合作者已证明，即使出现轻度的去相干，他的算法仍能正常工作。

量子计算机面临的另一个问题是纠错。可以用来记录和处理信息的各种系统都会受噪声的影响，噪声可能使信息位随机地翻转。经典的纠错方法是对信息位进行测量以确定其是否出错，但在量子计算机中这一方法会导致去相干。Ekert和Dentsch的研究小组证明，量子纠错原则上是可行的，但在实践中则很难实现。因此，即使量子计算机能够建造出来，它们或许也不能长时间地进行涉及许多位的量子并行计算。

为了超过现有的超级计算机分解因子的能力，采用Shor算法的量子计算机可能需要在数千步中跟踪数百位数据，同时始终保持量子相干性。鉴于Landauer已指出的一系列技术问题（包括去相干、激光脉冲的不可控制的变化，以及缺乏有效的纠错方法等 ），建造一台计算机来执行这样一种计算极有可能被证明是很困难的。然而，要超过量子系统的经典模拟，则只需要在数十步中跟踪数十位数据，这一目标就比较容易实现了。至于用量子逻辑来创造新奇的多粒量子状态并探索其性质,那是我们现在就能达到的目标。