互动科普

对微小金属团的研究有助于填补物理学家们对孤立原子和大块固体间有何差异这一认识上的空白。

加热一小块金属直至其开始蒸发。把金属蒸气通过一个细长的喷口吹入真空室中。这时会出现什么情况呢?喷入真空室的金属粒子将凝聚成微小的团，每个金属团含有从数个到数千个不等的金属原子。这些金属团比水滴和砂子小得多，它们构成了物质的一种引人人胜的新排列方式。 

虽然有关金属团的大多数实验涉及的是相当微小的物体，但是，原则上金属团可以是任意大的。因此，这些团聚物介于孤立的原子或分子与成块的固体或液体之间。在这个意义上，可以说它们是联系微观世界和宏观世界的一座桥梁。对于理论物理学家来说，金属团提出了许多饶有兴味的问题：为什么某些金属团比其它一些金属团稳定?需要有多少原子才能使金属团的性质开始接近于成块物质的性质?随着越来越多的原子聚集在一起，金属团的结构将发生什么样的变化? 

但是对金属团有兴趣的并不完全限于理论物理学家。例如，工业化学家从实践中得知，金属团可能是极好的催化剂。然而，在支配金属团的形成的基本原理被彻底弄清之前，可能难于更加有效地利用金属团。而在过去10年中，研究人员已越来越接近于实现了解金属团的形成这一目标。 

稳定性的魔术 

科学家们必须解释的一个金属团的根本特征就是为什么某些尺寸的金属团更容易出现。一百年以前，化学家们在构造元素周期表时遇到了一个类似的问题。当时他们发现，某些元素由于其原子拥有特定数目的电子而具有较高的稳定性。化学家们把拥有2个、10个、18个、36个和54个电子的气体元素称为“贵重气体”，因为它们的原子在化学上是惰性的，不与元素周期表中那些一般元素的原子起反应。在本世纪中，物理学家们发现，含有2、8、20、28、50、82和126个质子或中子的原子核格外稳定。因此，他们把这些数称为“幻数”。例如，铅有82个质子，其稳定性就异常之强。(铅的一种同位素有126个中子，因此被称为“双幻的。) 

结果发现，金属团中也存在幻数这种现象。1984年，伯克利加利福尼亚大学的一组研究人员考察了炽热钠金属形成的金属团。他们发现，含有8、20、40或58个原子的金属团的数目比其它尺寸的金属团要多得多。拥有这些数目原子的金属团之所以占据绝对优势，是因为由于某种原因它们的稳定性被证明是特别强的。 

物理学家们现在认识到，在足够高的温度下产生的不稳定金属团将释放出多余的原子，从而迅速地转变成较小而更稳定的金属团。实验人员发现，炽热钠金属形成的稳定金属团，其幻数序列接下去为92、138、198、264、344、442、554以及更大的数。具有这些原子数目的钠金属团(以及其它几种金属的金属团)甚至在它们热得无法固化、而仅以液态微滴的形式持续存在的情况下仍然保持稳定。 

金属团的这种倾向——即它们形成时的原子数目恰好为幻数——源于量子力学法则。根据量子力学，被束缚的电子只能具有某些能量。在孤立原子中，超过惰性气体原子中的电子数目的那些电子与原子核的结合是非常松散的，很容易离开原子核而逃逸掉。这些电子被称为价电子，不同元素的各种不同化学性质就是由价电子造成的。 

在金属原子组成的团中(或在一块更大的金属中)，这些价电子不再被束缚于它们原先所在的那些特定的原子上，而是相当自由地在原子间流动，此吋价电子被称为“去定域"(delocalized)。但是它们仍然呆在金属团中或在其周围，因为它们受到了它们所离开的原子现在所带的正电荷的吸引。（在价电子跑掉以后，原子核中的质子所带的正电荷不再被电子原先所带的等量的负电荷所抵销，这样先前中性的原子现在就变成了带正电的离子。） 

为了了解为什么某些数目的原子能使金属团具备稳定性，物理学家们的理想方案是希望确定金属团内部所有离子和价电子的详细组态，而这一点是非常难搞清楚的。但是，业已证明，物理学家们通过把一个金属团模拟为一块带正电荷的光滑“冻胶”一一价电子则被吸引到其上——就可以得到关于金属团的一些答案。（这一简化被称为“冻胶模型”(jelliummodel)). 

根据量子力学法则，这些电子的能量必定是量子化的——也就是说，能级只能取若干固定的值，永远也不会取这些固定值之间的值。在金属团中，也正如原子中一样，电子的可用能级并不是均匀分布的。能级组合成若干组，每一组内的各能级彼此较为接近，而各组之间则相隔比较远。由于历史的原因，原子内的这祥一组组的能级被称为电子壳层，尽管电子实际上并不局限于壳形区域中。量子力学法则限制了每一壳层中能容纳的电子的数目；如果电子完全填满了一个原子中的一个或多个壳层，那么这个原子就不会与其它原子起反应，因而是异常稳定的。这样，金属团的幻数的存在就有一定的道理了:这些幻数对应于完全填满金属团中的一个或多个壳层、从而使得金属团特别稳定的价电子的数目。（同样的机制也适用于原子核中被填满的质子和中子壳层，从而解释了其幻数的存在。） 

具有最大稳定性的金属团是近于球形的。然而，如果现有的电子不能把最高能级壳层按其最大容量填满，那么金属团就会变扁平或拉长，开始呈现类似于薄煎饼或橄榄球的形状。它也可能呈现一种更复杂的梨形、柠檬形或钻石的形状，或者是某种不具备任何对称性的构形。这类形状降低了金属团的总能量，从而使金属团更加稳定——虽然还不像那些其电子壳层被完全填满的金属团那样稳定。物理学家们很早以来就认识到，许多稳定的原子核也具有变形的金属团的部分理论工具是从核物理学先前的研究成果中得来的。 

超壳层

量子力学的形式化体系完全解释了金属团的电子壳层及其对应的幻数。但是对许多外行人来说，这一解释不是非常令人满意的。因为量子力学法则常常似乎与人的直觉相矛盾，而且很难直观地表示。幸运的是，借助于人们伺宏现物体打交道时的日常经验所对应的经典表述，我们可以获得对幻数的一定程度的了解。这种方法需要利用周期轨道论，该理论是科学家们在七十年初期提出来的，当时把它作为联量子力学与经典力学的桥梁.周轨道理论使物理学家们不费多力气就能够确定一个包含电子其它小粒子的系统中的主要壳的能量. 

为了直观地说明周期轨道理论如何应用于金属团设想为就是一个其内含有价电子的空心球，这些价电子以恒定的速度在球内沿直线运动.电子在球的内表面上反弹，其人射角等于反射角.(这个一般性的反射定律既适用于从镜子表面上反射的光波，也适用于从壁上反弹的粒子.)这个粗略的模型之所以有效，是因为价电子在金属团内基本上是自由自在地运动，但不能离开金属团。 

球形空腔内的周期轨道就是粒子能够遵循的运动轨迹:粒子可以沿着一条直径来回地弹射，也可以绕着有3个或3个以上的角的多边形运动。通过只考虑那些长度最短、出现最频繁的周期轨道，物理学家可以推导出允许能级的近似分布情况.3种最短的轨道是直径、三角形和正方形，但是，由于某些与几何性质有关的比较复杂的原因，直径轨道是出现得比较稀少的. 

仅使用三角形轨道和正方形轨道进行计算，所得出的能量壳层的模式在某种意义上是周期性的:如果把允许能级作为能量的函数绘出来，那么允许能级以均匀的间隔出现.但是，允许能级的重复出对形具彼两尺起存在两个不同姆蒎率，它们分别对应于两条占优势的轨道(即三角形轨道和正方形轨道)。正如两列具有相似频率的声波在重迭时会彼此干涉而产生频率较低的“拍”，两组壳层也会彼此干涉而产生大尺度的能级聚集现象。这样聚在一起的能级称为超壳层。 

原则上超壳层也应当出现于原子核中。但实际上原子核中并不存在超壳层，这是由于原子核从不会大到能够维持超壳层的地步：必须有800到1000个左右的粒子才能够产生第一个超壳层拍，而至今产生出来的最大的原子核其中子少于200个，质子则不到120个。但是超壳层实际上能够存在于大的金属团中。1991年，丹麦哥本哈根尼尔斯·玻尔研究所以及德国斯图加特马克斯·普朗克固态研究所的物理学家观察到了炽热金属团的超壳层。此后不久，法国奥赛Aime Cotton实验室的研究人员发现了锂金属团中存在超壳层的证据，而里昂第一大学(the Univensity of Lyon—I)的研究人员则检测到镓金属团中的超壳层。 

球形空腔模型的周期轨道理论预测，在相继的壳层之问，幻数的立方根(它大致相应于对应金属团的半径)增加一个相同的数量。而当研究人员绘图表示出对各种炽热金属团所观察到的幻数的立方根和壳层数之间的关系时，他们的确得到了一条直线，其斜率为0.61。这一结果与球形空腔的周期轨道理论的预测(0.603)基本相符，误差仅为1%左右.利用冻胶模型进行的更完全的量子力学计算得出的斜率恰好就是观测到的数值。(这一计算仅对于其原子数目在数千个以下的金属团是可行的，囚为尺寸更大的金属团所需要的计算时间太长了。) 

完美的多面体 

古希腊的哲学家柏拉图曾设想，物质的基本结构单元为正多面体，即所谓的柏拉图立体。说来也怪，对于冷的金属团，柏拉图的设想可能也错不到哪里去。当大量的金属原子(约1千个左右或更多)在比较低的温度下慢慢地聚集起来时，它们形成一些微小的立体，这些立体中的原子紧密地堆积成规则的几何形状，就象食品店中的一堆桔子那样。 

观察这些冷金属团的稳定性如何随它们的大小而变，物理学家们便能够推导出冷金属团的几何构形。1991年，马克斯·普朗克固态研究所的研究人员让钠原子在低温下凝聚，发现低温下形成的最稳定的金属回其大小与高温下形成的金属团完全不同。这就是说，低温下是完全新的一组幻数在起作用.这些研究人员很快得出这样的结论:新观察到的幻数对应于堆积成正二十面体的原子集合。(正二十面体有二十个面，各面为正三角形。) 

在这样一类实验中，当一层又一层的钠(每层只有一个原子厚)不断加上去时，正二十面体便越变越大，由此得到一个特殊的幻数序列。粗略地说，这些"原子壳层"类似于洋葱头的一层层的皮。通过这种方式形成的简单的多而体比不规则排列方式更稳定，因为当梭的数目达到最小值时，将原子保持在各自位置上所需的能量也随之降低。看来大自然偏爱正多面体的经济效率。 

以立方根的形式表示的冷金属团的幻数随原子壳层数目的增加而增加，但其增加的速率与热金属团阳电子能量壳层的增加而增加的速率不同。对于各种类型的冷金属团，上升的迅速程度(即斜率)是各不相同的。看来不同的斜率丧明存在着不同形状的正多面体。例如，对于冷的钠或钙金属团，其斜率为1.5左右，而它们最容易形成二十面体。含有同等数目的钠原子与碘原子或同等数目的钠原子与氯原子的金属团，其斜率正好为1.0。表明它们形成的是立方体。为什么会出现一种形状而不是另一种形状仍然多少是一个谜。 

冷的铝或铟金属团提出了一个特别令人感兴趣的难题。在画出它们的幻数的立方根随壳层数而变的函数关系图时，研究人员发现其斜率为0.220。这个斜率小于稳定电子壳层的斜率(0.6).但与原子堆集成正四而体、正八而体、正二十面体和立方体时的斜率均不相同(这四种情况下的斜率分别为0.50、0.874、1.493和1.0)。事实上，不可能找到这样一种正多面体，当用一层又一层的原子把它复盖起来时，它会得出研究人员在这些金属团上所观察到的那组幻数。 

斯图加特小组的成员提出了一个可能的解决方案——这种铝或钢金属团以正八面体的形状长，但是，当从一个幻数增大到下一个幻数时，增加的原予数仅足以一次复盖一个三角形面。这种情况将得出观察到的那个低缓的斜率。他们的解释看来似乎是正确的，但是此解释立刻又引出一个新的、迄今尚未解决的问题：为什么完整的正八面体的稳定性并不比那些只增加一个或两个三角形而的正八面体的稳定性高出多少? 

值得注意的是，原子堆集所产生的幻数并没有唯一地决定有关的多面体的形状。例如，与二十面体相关的幻数同立方一八面体(即各个角被切掉的立方体)中可能发现的幻数是相符的。对冷的钙金属团所进行的仔细研究已经向科学家们揭示出，形成的金属团是正二十面体。但是我们韭不能肯定这一点——任何人都没有直接看到过这些正二十面体。原则上说，如果最大的金属团处于静止状态，则可以用一台电子显微镜观察这些金属团。问题在于，自由金属团是在迅速运动着的原子束流中形成的，不可能使它们停下来以拍摄它们的图象而又不改变它们的形状。 

竞争能手 

在大量原子构成的金属团中，两类壳层(即电子能量壳层和形成正多而体的原子壳层)都力争能够左右金属团的形状和稳定性。大小和温度对于决定哪种类型的壳层占优起着关键的作用。但是，测量在束流中运动着的孤立金属团的温度是非常困难的：人们甚至可以对这种情况下究竟是否能够定义温度提出疑问。严格地说，温度这一概念仅对于处于热平衡状态的许多粒子构成的系统有意义。但是大多数金属团实验并没有实现这一条件，而是束流巾形成的每个金属团各走各的路，不受邻近金属团的影响。这些孤立的金属团并没有达到热平衡状态。这样，由于无法把一只温度计伸到所考察的微小金属团上——这在实验上是不可能做到的事——因而不存在测定其温度的简单方法。 

但是，变化的趋势是很清楚的。在受到严密控制的条件下加热束流源的喷嘴，冷的钠金属团中整齐堆集的正二十面体壳层似乎就消失了。这一转变可能相当于固态金属团的熔化。在这种情况下，熔化的温度取决于金属团的大小。 

研究人员发现铝构成的金属团中也存在一种类似的转变过程。当束流源的温度超过500开氏度时——此温度仍远远低于大块铝的熔融温度——幻稳定的金属团其尺寸的立方根与壳层数之间的函数关系图便不再具有0.220的斜率(这一斜率表明原子堆集在正八面体的面上)。此时这些函数关系图的斜率为0.6左右，而这是电子壳层的典型斜率。看来有理由推测，这些金属团已变成熔融状态，尽管喷嘴处的温度远低于火块金属的熔点。不过这一结论可能过于简单化了：同温度一样，对于这样微小尺寸的物体，固体和液体之间的相变概念本身也是成问题的。或许在这种情况下金属团的表而正在发生局部熔化，此熔化足以破坏由离子的堆集所左右的结构，从而使得完全的电子壳层所赋予的稳定性占据优势地位。 

弗雷堡大学的物理学家最近观察到一种稍有不同但是相关的相变。为了更好地掌握小的钠金属团的温度，他们采用了一个巧妙的策略。他们将金属团置于氦气中，而对于氦气他们是能够非常精确地调节其温度的。氦原子与钠金属团的这一混合物中将发生频繁的碰撞。然而，由于氦是惰性气体(也就是说它始终没有什么化学活性)，它不会改变金属团的结构——至少在不太高的温度下是如此。这样氦就提供了一种能实现热力学平衡的环境。 

在这种情况下，科学家们考察的不是幻数，而是具有某一固定尺寸的钠金属团吸收激光的方式。激光吸收的概率与激光频率之间的相关关系(吸收频谱)，可以揭示有关受激光照射的粒子的物理状态的许多信息。特别是，冷的刚性分子和热的液态微滴的吸收频谱是不同的。当温度在100开氏度以下时，实验人员观察到一个有许多尖峰的频谱，这正是刚性分子的典型吸收谱。而当温度在380开氏度以上时，实验人员发现其频谱只有两个比较宽的峰，它们的位置正是理论上对无结构的冻胶型金属团所预测的吸收峰位置。 

对于最小的金属团(此种金属团的内部结构始终起着重要的作用)，可以进行严密的、把每个原子中的所有电子都考虑进去的量子力学计算。这些量子力学计算揭示了金属团的详尽的分子结构，并能够对金属团的稳定性给出非常精确的描述。对于有几百个原子或更多原予的较大金属团，进行这类计算需要耗用太多的计算时间，这样物理学家们不得不借助于冻胶模型。对于有成千上万个原子的金属团，研究人员必须放弃量子力学，转而利用简化的周期轨道理论或依靠通过实验发现的幻数所提供的间接信息。 

自1984年以来，科学家们在认识和扩充金属团的幻数序列方而已经取得了长足的进展。有的实验已经产生了由多达2万1千个原子构成的正二十面体钠金属团。然而很明显的是，大块的钠中韭不含有这类二十面体结构。事实上，任何块状物质都不能够通过正二十面体的堆集而构造出来。正如人们不可能用正五边形的铺砖来复盖整个平面一样，正二十面体也缺乏必要的对称性，无法通过填满整个空间而形成扩展的三维品体。因此，即使是至今所产生出来的最大的钠金属团，其原子的排列方式也完全不同于大块的钠中原子的排列方式。 

人们研究金属团的最初动机，部分在于想要确定究竟需要多少个原子才能使得一团极微小的物质能具备大块固体的性质。关于金属团以及使金属团达到稳定的幻数尺寸，物理学家们现在已经有了许多的了解。然而，我们仍然不知道下面这个根本问题的答案：向大块固体的转变究竟发生于何时，以及是怎样发生的。目前我们能够说的只是，我们所研究过的金属原子团构成了一类令人惊异地独特的物质排列方式，这类排列方式肯定还会有许多东西令我们大开眼界。

 冷金属团的堆集 

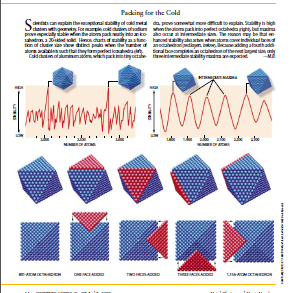
科学家们可以用几何结构来解释冷金属团的异乎寻常的稳定性。例如，当钠原子整齐地堆集成二十面体(有二十个面的立体)时．冷的钠金属团是特别稳定的。因此，稳定性随金属团尺寸而变的函数关系图上有一些清晰的尖峰，在这些尖峰处。可用原子的数目使它们恰好能形成正二十面体(左)。

冷的铝金属团——它们的原子堆集成微小的八面体—性质更难于解释。当铝原子堆集成正八而体时。它的稳定性很高(右)。但是当金属团的大小为相邻正八面体之间的某些中间值时。其稳定性也达到极大值。这一现象的原因可能在于，当铝原子复盖了正八面体的某一面时(下图中的红色原子层)，金属团的稳定性也得到增强，由于加上额外的第四个面就构成了下一个尺寸最大的八面体。因此可以预计在两个完全的正八面体之间只有3个稳定性极大值。 

图2简化的金属团模型把金属团描述为电子在其内不停地反弹的空心球(右图)。借助于周期轨道理论，物理学家们可以计算出电子的近似能级(水平条线)。两类最重要的周期轨迹(三角形和正方形)相互干涉。产生出聚集在一起的壳层，称为超壳层(supershell)。超壳层的模式可以在实验巾和更复杂的理论模型中见到(下). 

图3金属团的大小——以金属团中原子数目的立方根表示——始终随着壳层的增大而增大。但是增大的速率(斜率)与金属团束流的温度有关。冷的钠原子金属团的壳层是由紧密堆积的原子构成的正二十面体壳层。这种几何形：产生的特征斜率约为1.5。相反，炽热钠金属团的形状是由电子壳层决定的。而电于壳层则产生0.6左右的斜率。（图中壳层数为14的地方所体现的错开是由超壳层的效应造成的。周期轨通理论对这一现象给予了很好的解释。） 

图5激光的光吸收频谱揭示。随着温度上升，金属团从刚性分子转变成无结构的物体。对于保持在低温下的钠金属团，光子吸收概率随激光频率的不同而发生显著的变化(蓝色阴影)。这正是分子所特有的一种性质。但在高温下(桔红色阴影)，频谱逐渐变得平滑，只有两个比较宽的峰。这与物理学家对于缺乏内部结构的金属团使用的所谓冻胶模型是一致的。