互动科普

在正在形成和发展的万物理论中，不仅是弦，而且薄膜和黑洞也起着一定的作用。

在某些权威人士以所有的重要发现均已告完成为由而预测科学即将走到尽头之时，值得强调指出的是二十世纪物理学的两大支柱——量子力学和爱因斯坦的广义相对论——是互不相容的。广义相对论违背了支配基本粒子行为的量子力学法则，而在另一极端尺度上，黑洞则向量子力学的基础本身提出了挑战。必须作出某种重大的让步。这一困境与其说是预兆着那些杞人忧天的千年纪预言家们声称将出现的成果不断递减的悲观前景，不如说是预兆着一场新的科学革命的来临。

直到最近，人们都是把构筑万物理论——即把引力和量子力学统一起来韭描述所有物理现象的一种理论——的最大希望寄托在弦上。所谓弦，就是其振动方式代表了各种基本粒子的一种一维物体。然而，在过去两年中，弦已经被纳人了M理论(M-theory)的麾下。据弦理论的鼻祖、普林斯顿高级研究所的Edward Witten(他被《生活》杂志评为美国第六位最有影响的二战后一代人物)说：“M在这里可以代表魔术(Magic)、神秘(Mystery)或薄膜(Membrane)，随你的喜好而定。”有利于这一理论的新证据与日俱增，它是自从弦理论首次登场以来所取得的最激动人心的进展。

同弦理论一样，M理论赖以成立的关键是超对称这一概念。物理学家根据粒子的内禀角动量(即“自旋”)把粒子分为两大类。超对称性要求，对于每一种具有整数自旋——0，1，2等等，以量子单位表示—的已知粒子，均存在一种质量相同但自旋为半整数(1／2，3／2，s／2等等)的粒子，反之亦然。

遗憾的是，至今尚未发现任何一个这样的超对称对应粒子。这种对称性即使存在，必定也已破缺，因此推测存在的那些粒子其质量与已知粒子的质量韭不相同。它们的质量太大，无法在现有的加速器中探测到。即使如此，理论家们对超对称性仍然坚信不疑，这主要是因为超对称性提供了一个可以使弱力、电磁力和强力同最难捉摸的一类力——引力相统一的框架。

超对称性对空间和时间的坐标作了变换，使物理法则在所有观测者看来都是相同的。爱因斯坦的广义相对论根据这一条件而导出，因此超对称性蕴含了引力。事实上，超对称性预测存在着“超引力”，其中引力相互作用由一种自旋为2的粒子——引力子——传递，而引力子的对应粒子为“引力微子”(gravitino)，其自旋为3／2。

传统的引力未对可能的时空维数规定一个上限：原则上时空的方程可以建立在任何维数上。超引力的情况则不相同，它给时空维数规定了一个上限——11。当然，人们熟悉的宇宙有3个空间维(即长、宽和高)，时间则构成了时空的第四维。但在本世纪二十年代初，波兰物理理学家Theodore Kaluza和瑞典物理学家Oskar Klein提出，时空可能还有隐蔽的第五维。这个额外的维与其它的维不同，它不是无限的，而是卷绕起来形成一个圆圈。量子波可以围绕着此圆圈恰好形成一个环。围绕着这个圆的波必须是整数个，其中每一个对应于一种具有不同能量的粒子。因此这些能量是“量子化”的，即离散的。

然而，生活在另外四维中的观测者看到的将是一组具有离散电荷而不是离散能量的粒子。电荷的量子(即单位)取决于上述那个圆的半径。在现实世界中，电荷也是量子化的，其最小单位为e(电子所携带的电荷)。为了得到正确的e值，该圆必须是极其微小的，其半径约为10-38厘米。

这一看不见的维的极小尺度说明了为什么人(乃至原子)不会觉察到它的存在。即使如此，它仍产生出电磁场，而已经存在于四维世界中的引力则将与电磁力统一。

1978年，巴黎高等师范学校的Eugene Cremmer，Bernard Julia和Joel Scherk意识到，超引力不仅允许多达7个额外的维存在，而且它在11维的时空中(10个空间维和一个时间维)将是最精巧最完美的。该理论最终预测的那类现实的4维世界取决于这些额外的维是如何按Kaluza和Klein的方式卷绕起来的。可以设想，这几个卷绕起来的维使物理学家能够推导出除电磁力外还存在强核力和弱核力。由于这些原因，许多物理学家开始探讨11维中的超引力，期望它可能就是人们追求的统一理论。

然而，1984年，11维超引力理论的支柱突然一下倒塌了。现实世界的一个重要特征是，自然界对于左和右是加以区别的：支配弱核力的法则在镜象反映中将变得不同。(例如，中微子的自旋始终是左手的)。但是Witten和其它一些研究人员强调指出，在把时空从11维简化到4维时，无法轻易地推导出这样一种“手征性”来。

P维膜

于是超引力的地位被1O维空间中的超弦理论取而代之。曾有5个互相对立的理论风行一时：这5个理论根据其数学特征而分别命名为E8×E8异型弦(11eterotic)，SO(32)异型弦、I类SO(32)，ⅡA类及ⅡB类弦。(I类弦是“开型弦，它仅由一条线段构成。而其它各种弦则是形成环的“闭合”弦。)特别是其中一种弦——E8×E8——似乎能够解释已知的基本粒子和力(包括它们的手征性)，至少在原则上能够解释。与超引力不同的是，弦看来提供了一种与量子效应相容的引力理论。所有这些优点使得弦理论令物理学家们为之倾倒，而11维的超引力理论则被打入了冷宫。加利福尼亚理工学院的Murray Gell Mann在一次会议上宣称：“11维超引力理论见鬼去吧!”这概括地说明了人们当时的情绪。

然而，在对弦理论的最初那股狂热情绪过去之后，怀疑态度开始滋生起来。首先，许多重要问题——特别是如何通过实验来检验该理论——似乎无法用传统的计算方法加以回答。这类问题需要用全新的方法来解决。其次，为什么会有5种不同的弦理论?如果人们寻求的是一种独一无二的万物理论，那么理论过多显然是件使人感到棘手的事。第三，如果超对称性允许有11维，为什么超弦就只到10维为止?最后，如果我们要把类点粒子看成弦，那为什么不把它们看成是薄膜，或更一般地看成是P维物体?(按惯例把它们称为P维膜(p-brane))。

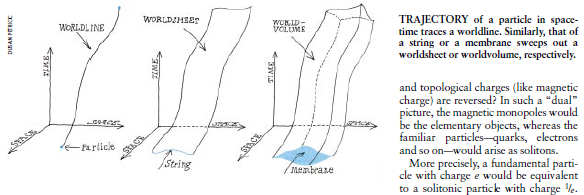
因此，当大多数理论家们正对超级细面条吃得津津有昧之时，一批人数虽少但劲头十足的科学家却对超级有馅包子产生了胃口。一个维数为零的粒子在时空中演变时扫描出一条一维的轨迹，即所谓“世界线”(worldline)(见图2)。类似地，一根弦——它具有一维，即长度——扫出一个2维的“世界面(worldsheet)，而一张薄膜一它具有2维，即长和宽——则扫出一个3维的“世界体”(world volume)。一般地，一个P维膜将扫出一个P+1维的世界体。(当然，必须有足够的空间使P维膜能够在时空中四处移动，因此P+1的值不能超过时空的维数)。

早在1962年，量子力学的奠基人之一Paul A．M．Dirac(狄拉克)就已构建了一个以薄膜为基础的富有想象力的模型。他作了这样一个假定：电子实际上不象一个点，而是一个微小的气泡，即包绕起来的薄膜。狄拉克认为，它的振荡可能产生如μ子之类的粒子(μ子是比电子重分别扫出一个世界面或世界体的类电子粒子)。虽然狄拉克的尝试没有成功，但他提出的薄膜方程实际上就是我们今天使用的方程。薄膜可以采取气泡的形式，也可以象一块橡皮那样沿着两个方向拉伸开来。

超对称性给P维膜的可能维数施加了严格的限制。格罗宁根大学的Eric Bergshoef，现在在得克萨斯农业与机械大学的Ergin Sezgin，以及剑桥大学的PaulK．Townsend从数学上发现了一种存在于11维时空中的薄膜。它仅有两个空间维，看起来象一张纸。伦敦国王学院的Paul S．Howe，京都大学的TakeoInami，伦敦帝国学院的Kellogg Stelle以及本文作者得以证明，如果这11维中有一维是一个圆，那么我们就能把薄膜围绕这个圆包起来二次，将其边缘粘在一起而形成一根管。如果圆的半径变得足够小，那么卷起来的薄膜最终看起来就象1O维空间中的一根弦。事实上它恰好得出ⅡA类超弦。

尽管取得了这样一些结果，但研究薄膜的工作仍然基本上被正统的弦理论界所忽视。幸运的是，由于在一个表面上看来不相关的领域中所取得的进展，情况即将有所改观。

1917年，德国数学家Amalie Emmy Noether证明，由于对称性的缘故，基本粒子的质量、电荷及其他特性一般是守恒的。例如，如果假定物理学的定律不随时间而变(也就是当时间消逝时这些定律是对称的)，那么就可以推出能量是守恒的。而电荷守恒则可以从粒子波函数的对称性推导出来。

然而，有时粒子的特性可以因场的变形而得到保持。这类守恒定律称为拓扑的，因为拓扑学是研究物体形状的数学分支。这样，一组场力线中的一个结(称为孤子)可能碰巧无法被弄平滑。其结果是孤子不会消散，其行为很象一个粒子。孤子的一个经典例子是磁单极子(即条形磁铁的孤立的一极)。磁单极子在自然界中还没有被发现，某些场理论预测它就是以卷绕形态存在的一种孤子。

这样，按照传统的观点，电子和夸克之类的粒子(它们携带Noether荷)被认为是基本的，而磁单极子之类携带拓扑荷的粒子则是衍生的。然而，1977年，Claus Montonen(现在在赫尔辛基物理研究所)和DavidI Olive(现在在威尔士大学斯旺西分校)作出了一个大胆的猜想。是否可能存在另一种物理学表达方式，其中Noether荷(如电荷)与拓扑荷(如磁荷)的作用颠倒过来呢?在这样一种。对偶(dual)模式中，磁单极子将是基本粒子，而人们熟悉的粒子——夸克、电子等——则将以孤子的形式出现。

更确切地说，具有荷e的基本粒子将等价于具有荷1／e的孤子．由于一个粒子的荷是对它的相互作用的强度的量度，因此，如果原始粒子的相互作用较强(也就是说e的值较大)，那么单极子的相互作用就较弱，反之亦然。

这一猜想如果正确，将得出一项深刻的数学简化。例如，在夸克理论中，如果夸克的相互作用较强，物理学家们就几乎无法进行任何计算。但是此理论中的任何单极子必定都只具有较弱的相互作用。我们可以设想用基于单极子的对偶理论进行计算，从而自动得到关于夸克的所有答案，因为对偶理论将给出相同的最终结果。

遗憾的是，这一设想始终未能实现。它属于一类。先有鸡还是先有蛋的问题。Montonen Olive猜想一旦得到证明，就可以超越常规的计算方法，但这一猜想首先必须通过其它某种方法加以证明。

结果表明，p维膜也可以看作是孤子。1990年，圣巴巴拉理论物理研究所的Andrew Strominger发现，一根10维的弦可以产生一个5维膜的孤子。Strominger提出，强相互作用的弦是弱相互作用的5维膜的对偶等价物，这就使我提出的一个更早的猜想得以卷土重来。

这一对偶性存两个重大问题。首先，Montonen和Olive提出的对偶性——即通常的4维空间中电与磁之间的对偶性——还没有得到证明，因此10维空间中弦与5维膜之间的对偶性就更不容易站住脚了。其次，关于如何发现5维膜的量子性质(因而证明新的对偶性)，存在着各种各样的问题。

不过，由于孟买塔塔基础研究所的Ashoke Sen证明了超对称理论规定必须存在某些既有电荷、又有磁荷的孤子，因此上述障碍中的第一个已被消除。Montonen Olive猜想已经预测了这类物体的存在。这一看起来似乎不引人注意的结果使许多持怀疑态度的人转变了看法，韭导致一大批论文的涌现。特别是，此结果启发卢特格斯大学的Nathan Seiberg和Edward Witten去寻找更现实的(虽然仍是超对称的)一类夸克理论中的对偶性。他们提供了就在几年前还是不可想象的有关量子场的大量信息。

对偶性的对偶

199o年，若干理论家把Montonen Olive对偶性的概念推广到4维超弦。在4维超弦的范围内此概念变得更加自然。这种对偶性获得了S对偶性的名称，不过它仍然是推测性的。

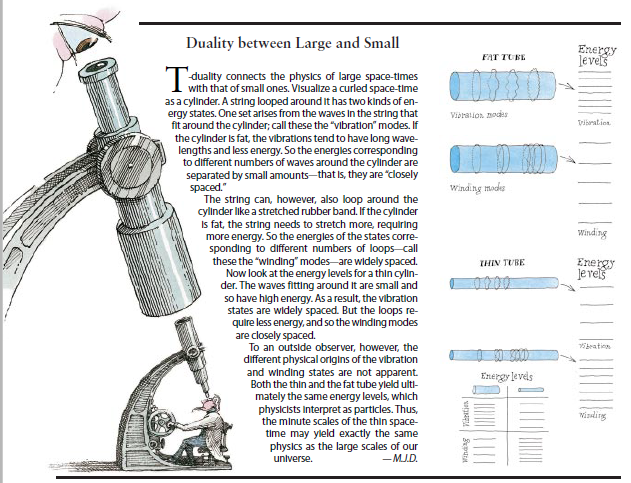
事实上，弦理论家们已经对完全不同的一类对偶性(称为T对偶性)习以为常。T对偶性把一根弦绕着一个紧致维形成环圈时所出现的两类粒子联系起来。一类粒子(称其为“振动”粒子)类似于Kaluza和Klein所预测的粒子，它们产生于弦环圈的振动(参看图6)。如果圆很小，这类粒子的能量就更大。此外，弦能够绕着圆转许多圈，就象一根橡筋可以绕着手腕转许多圈一样。弦环绕的次数越多，圆的半径越大，那么弦的能量就越高。而且每一能级都代表一个新的粒子(称它们为环绕粒子(winding particle))。

T对偶性认为，半径为R的圆的环绕粒子与半径为1／R的圆的。振动粒子是相同的，反之亦然。在物理学家看来，这两组粒子是不可区分的：较粗的紧致维和较缌|的紧致维可以产生看起来完全相同的粒子。

这种对偶性具有深刻的意义。几十年来，物理学家们一直在努力了解接近普朗克长度的极小尺度上的自然界性质．我们一直猜想，我们所知道的自然法则在更小的距离上将不再成立．然而，T对偶性却提示，在这样小的尺度上，宇宙看起来仍同大尺度上的情况一样。人们甚至可以想象．如果宇宙缩小到小于普朗克长度，那么它将转变成一个对偶宇宙，后者随着原先那个宇宙的缩小而不断增大。

但是，由于存在着使5维膜量子化的问题，弦和5维膜之间的对偶性仍然是猜测性的从1991年开始，得克萨斯农业与机械大学的一个研究小组——包括Jianxin Lu，Ruben Minasian，Ramzi Khuri和本文作者——设法避开了这个问题，从而使它得到解决。如果10维中的4个维卷绕起来，而5维膜包着这4个维，那么后者最终就成为一个一维物体，eP．6维时空中的一个(孤子)弦。此外，10维中的基弦(fundamental string)即使在6维中仍然是基本的。这样弦和5维膜之间的对偶性这一概念就让位于另一个猜想，即孤子弦和基弦之间的对偶性。

这样做的好处在于我们确实知道如何使弦量子化。因此，可以对弦一弦对偶性的预测进行检验。例如，人们可以证明，孤子弦相互作用的强度是由基弦相互作用强度的倒数给出的，完全符合上述猜想。

1994年，玛丽女王和威斯特菲尔德学院的Christopher M．Hull同Townsend一起提出，弱相互作用的异型(heterotic)弦甚至可能是强相互作用的ⅡA类弦的对偶，如果这两类弦都在6维中的话。把不同的弦理论分隔开来的壁垒开始逐渐倒塌了。

当时我想到弦一弦对偶性还有另一个出乎意料的附带好处。如果我们通过把两个维卷绕起来而使6维时空减少到4维，那么基弦和孤子弦就各获得一种T对偶性。然而奇迹正好出现在这里：孤子弦的T对偶性正好就是基弦的S对偶性，反之亦然这一现象一种场合中荷的交换就是对偶场合中长度的反演——称为对偶性的对偶(Duality of Dualities)。它使先前纯属猜测性的S对偶性有了和业已成熟的T对偶性一样坚实的基础。此外，它还预测，物体相互作用的强度——它们的荷——与看不见的维的尺寸有关。在一个宇宙中表现为荷的东西在另一个宇宙中可能表现为尺寸。

1995年，Witten在南加利福尼亚大学作了一次具有里程碑意义的演说。在演说中他一下子把关于T对偶性、S对偶性以及弦一弦对偶性的所有工作全都归于11维的M理论之下．随后的几个月中，因特网上出现了足足数百篇论文，这些论文证实，无论M理论是什么，它肯定都将以一种相当重要的方式涉及到薄膜。

甚至连E8×E8弦——它的手征性曾被认为是不可能从11维推导出来的——也在M理论中找到了起源。Witten同普林斯顿大学的PetrH0rava一起，说明了如何使M理论中额外的维收缩成一条线段。这样所得的图景是两个通过11维时空连系起来的1O维宇宙(线段每端各有一个)。粒子——以及弦——仅存在于位于两端的平行宇宙中，它们只能通过引力彼此联系。(人们可能猜想，我们宇宙中的所有可见物质位于一面墙上，而所谓“暗物质——据信它可以解释宇宙中的不可见质量——则存在于另一面墙上的平等宇宙中。)

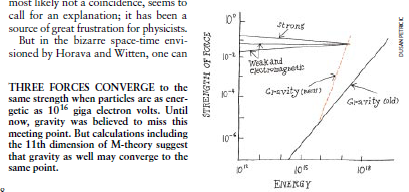
这一图景对于通过实验检验M理论可能具有重要的意义．例如，物理学家们知道，所有各种力的内禀强度都随相关粒子的能量而变．在超对称理论中，人们发现，强力、弱力和电磁力的强度会聚于1016千兆电子伏的能量E上。此外，这些力的相互作用强度几乎等于——但不完全等于——无量纲数GE2的值(G为牛顿引力常数)．这一不相等但又极为接近的情况极有可能并非巧合，看来需要对它作出解释．这一直是令物理学家们感到极为失望的一个问题．

但是，在Horava和Witten所设想的奇异时空中，人们可以选择第11维的尺寸，使所有4种力均会聚于这一共同的尺度上．它远小于普朗克能量(1019千兆电子伏)，而人们先前曾预计引力在普朗克能量上将变成较强的力。(量子力学把高能量同短距离联系起来．因此普朗克能量就是以能量表示的普朗克长度。)这样，量子引力在能量上与日常事件的接近程度就比物理学家们先前所认为的大得多，这一结果对宇宙学将产生全面的影响．

最近，圣巴巴拉理论物理研究所的Joseph Polchinski意识到，某些P维膜类似于十九世纪德国数学家Peter G. L．Dirichlet发现的一种表面。有时这些薄膜可以饵释为黑洞，．或者更确切地说是黑膜(black-brane)，即任何东西(甚至光)都不能从中逃逸出的天体。

例如，开型弦(open string)可以被看作是有一部分隐藏于黑膜后面的闭合弦(closed string)．这些突破已导致人们对黑洞作出新的解释，即把黑洞看成是包着7个卷绕维的相交的黑膜。因而有人强烈地倾向于认为，M理论甚至可能解决剑桥大学的Stephen W．Hawking提出的黑洞悖论。

1974年。Hawking证明黑洞监不完全是黑的：它可以辐射出能量。在这种情况下，黑洞必定有熵(熵通过统计可用量子态的数目来衡量一个系统的无序程度)。但是这些量子态的微观起源仍是一个谜。哈佛大学的Strominger和CumrunVafa借助于Dirichlet膜的方法统计了黑膜中量子态的数目．他们发现的熵与Hawking的预言完全符合，这是M理论取得的又一项卓越成就．

黑膜也有希望解决弦理论的最大问题之一：把10维减少到4维的方式看来有数十亿种之多．这样多的方式产生了关于真实世界运行机制的许多互相对立的预测——换言之也就是根本没有预测。然而，业已证明，当黑膜包绕着的一个洞收缩时，黑膜的质量可能消失．这一性质对时空本身有着神奇的影响，使一个具有一定数目的内部洞的时空(类似于Gruyere奶酪)能够变为另一个具有不同数目的洞的时空，从而违背了经典拓扑学的法则．

如果所有的时空都通过这样的方式联系起来，那么寻找一个合适的时空就成了比较容易对付的问题．弦最终可能选择一个具有比如说最低能量的时空，并在这个时空中存在下来．然后，弦的波动就将产生出我们现在所知道的基本粒子和力，也就是真实的世界。

由10到11：不算太晚

尽管取得了所有这些成就，物理学家们仍然只不过窥见到M理论的一些皮毛而已。这个理论的主要图景仍未露面。最近，卢特格斯大学的Thomas Banks和StephenH．Shenker同得克萨斯大学的Willy Fischler以及斯坦福大学的Leonard Susskind一起，提出了M理论的一个严格定义。他们的。矩阵理论的基础是无穷多个零维膜(也就是粒子)。这些粒子的坐标(即位置)不是通常的数，而是不具有交换性的矩阵——即xy不等于yx。在这个模型中，时空本身是一个模糊的概念，其中坐标不能够定义为通常的数，而是被定义为矩阵．

物理学家们很早以来就一直猜想，把引力——换言之就是时空的几何特性——同量子力学统一起来的工作将会使时空变成类似地不严格定义的东西——至少在新的定义被发现之前是这样．矩阵方法使人们大为振奋，但看来还不是最终的’解决办法．在今后几年中，我们希望能发现M理论的真面目．

Witten喜欢想象在另外一个行星上物理学将会如何发展起来，那个行星上的人作出广义相对论、量子力学和超弦之类的重大发现的顺序将和地球上不同．类似地，我也想说，在比我们的地球更有逻辑性的其它行星上，11维可能是研究的出发点，而10维的弦理论则是随后．从11维中衍生出来。实际上，在未来地球上的历史学家们看来，二十世纪后期的理论家们好象是一群在海滩上玩耍的孩子，被各种各样更圆滑的超弦卵石和更漂亮的超弦贝壳所吸引，而同时却有一片M理论的汪洋大海就在他们前面未被发现．

图1时空中一个粒子的轨迹描画出一条世界线。类似地，一根弦或一个薄膜的轨迹分别扫出一个世界面或世界体。

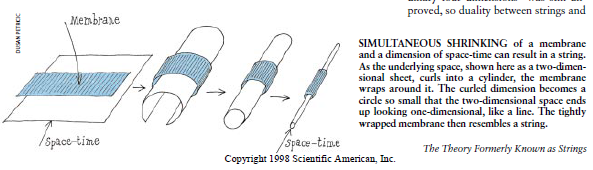
图2一个薄膜和时空的一维同时收缩能够产生一根弦。当基底空间——图中用一张两维的纸表示——卷绕成一个圆筒时．薄膜就把它包绕起来。这个弯曲的一维收缩成一个极小的圆．以致2维空间最终看起来就象是一维的直线一样。而紧紧卷绕起来的薄膜这时就类似于弦。

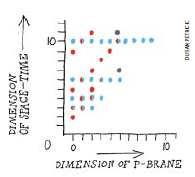
图3。膜扫描(brahe scan)列出了在不同维的时空中出现的膜。雠的P维膜是粒子，1维的p维膜是弦，2维的P维膜类似一张纸或一个气泡．有的膜没有自旋(红色)，但Dirichlet M自旋为1(蓝色)．

围5当粒子的能量高达1016千兆电子伏时，三种力就会聚于同一强度上，直到现度ID叶在之前，人们一直认为引力偏离了这个会聚点。但是，把M理论的第l1维考虑进去后进仔的计算，表明引力也可能会聚于这。同一点上。

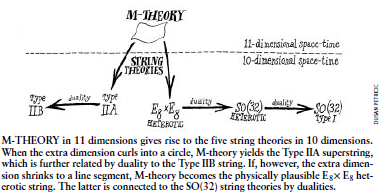
图6 11维中的M理论产生了10维中的5个弦理论。当这额外的一维卷曲成一个圆时，M理论就给出了ⅡA型超弦，此超弦又通过对偶性而与ⅡB型弦联系起来。然而，如果这额外的一维缩小成一条线段，那么M理论就变成了物理上可能的E8XE8异型弦。后者又通过对偶性同SO(32)弦理论联系起来。