互动科普

在黑暗中窥视的量子

Paul Kwiat*, Harald Weinfurter**, Anton Zeilinger

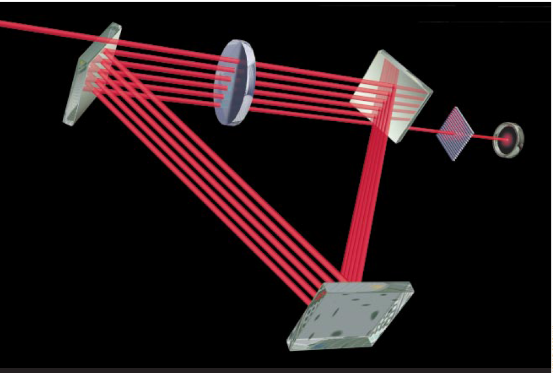
量子光学证明，无相互作用的测量——即在没有光线或其它任何东西射到物体的情况下探测到物体——是存在的。

在希腊神话中，英雄柏修斯面临一个无人羡慕的差使——与可怕的美杜莎搏斗。这个蛇发女妖怪的魔力简直骇人听闻：任何人只要盯她一眼，这个倒霉的观看者立刻就会变成石头。这个故事的一种说法是，柏修斯巧妙地用他的护身盔甲把美杜莎的影像反射到这个怪物自己身上，从而把她变成石头，自己则得以避免了这个不幸的结局。但是，如果柏修斯没有配备磨得很光亮的盔甲，情况又会怎样呢?那他大概就死定了。如果他闭上双眼，就无法找到他的目标。如果他哪怕是稍微窥看一下，也会有少量的光在碰到美杜莎后反射到他的眼中。象这样“看见”妖怪后，他就完蛋了。

在物理学界中，这一困境可以总结为发明全息术的诺贝尔奖金获得者Dennis Gabor在1962年提出的一个看起来无可指责、几乎是不言自明的说法。Gabor的说法实质上就是，如果射到被观测的物体上的光子(光的基本粒子即光量子)少于一个，则不可能进行任何观测。

然而，过去几年中，在越来越怪异的量子光学这一领域从事研究的物理学家们已经弄清，这种说法不但远不是不言自明的，而且是不正确的。因为我们现在已经知道了如何在没有光子碰到一个物体的情况下判定它的存在。

这类无相互作用的测量似乎是自相矛盾的——如果没有相互作用，怎么可能进行测量?在经典力学中，这是一个合情合理的问题。(经典力学是描述足球、行星及其它不太小的物体运动规律的物理学分支。)但量子力学—研究电子、光子和原子世界中其它粒子的科学—却不同。量子力学加上巧妙的实验设计的确能实现无相互作用的测量。如果柏修斯具备量子力学的知识，他可以想出一种办法来“看见”美杜莎，同时却没有任何光线真正射到这个女妖怪身上然后又进入他的眼中。他可以做到“不看而看”。

这类量子戏法启发人们产生多种设想来建造可能具有实际用途的检测装置。或许更令人感兴趣的是它那玄乎其玄的哲学含义。这些用途与意义最好是在假想实验这一层次上来认识。假想实验就是简练的实验分析，它包含了真实实验的所有基本要素，但又免去了实际进行实验的种种复杂情况。

这样，作为假想实验，试考虑一种用贝壳来玩的打赌游戏。它使用两个贝壳和一块石子，此石子藏在一个贝壳下。然而，这个石子却是非常特殊的石子：只要一见光，它就会变为灰尘。游戏者要确定石子藏在哪个贝壳下，但却不能让它见光，也不能用其它任何方式扰动它。如果一位游戏者让石子变成了灰尘，他就输掉了这场游戏。

这一任务初看起来是不可能完成的，但是我们很快就看出，如果游戏者情愿只有一半的机会获胜，那么就有一种很简单的办法：拿起那个他希望不含石子的贝壳。如果正合他所望，那么他就知道石子在另一个贝壳下面，即使他并没看见那个贝壳。当然，用这种方法取胜纯粹不过是碰运气而已。

然后我们对游戏作进一步的修改，这个修改似乎是简化了此游戏，然而实际上却是使局限于经典物理世界的游戏者无获胜的可能。我们只有一个贝壳，这个贝壳下有石子还是没有石子完全是随机的。游戏者的目标是确定贝壳下面是否有石子，但同样不能让它暴露于光线下。

假定贝壳下藏有一个石子。如果游戏者不查看贝壳的下面，那他就不会得到任何信息；如果他看了贝壳下面，那他就知道石子曾在那里。不过他在这样做时肯定会使石子暴露于光线下，因此他看见的仅是一堆灰尘而已。游戏者可能会尝试减弱光线使得它只有极小的机会

射在石子上。然而，为了使游戏者能看见石子，至少必须有一个光子射在石子上，根据定义，这就意味着他输掉了游戏。

Elitzur、Vaidman和炸弹

为了使这一游戏更富戏剧性，特拉维夫大学的物理学家Avshalam C. Elitzer和Lev Vaidman把石子设想为一颗“超级炸弹”，只要有哪怕一个光子射到它，它也会爆炸。这样问题就变为：确定一颗石头炸弹是否藏在贝壳下，但不要把它引爆。

Elitzer和Vaidman是第一次提出这个问题的答案的研究人员。他们的答案至多在一半的时间中是有效的。然而，为了证明真正有希望赢得这场游戏，该答案是必不可少的。

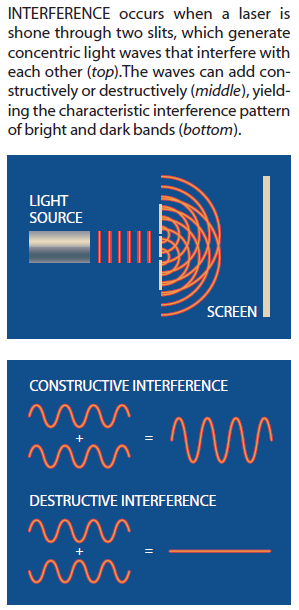
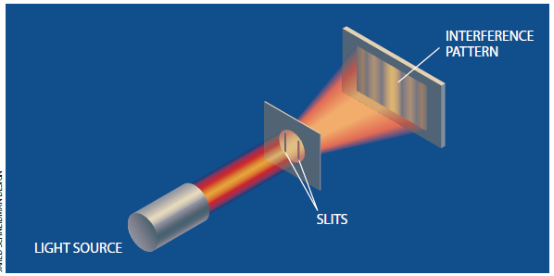
他们的方法利用了光的基本性质。我们已经提出，光是由光子组成的，这使人想起它具有类似粒子的特性。但光也可以显示明显的波动特性——特别是一种称为干涉的现象。干涉是两列波彼此迭加的方式。例如，在著名的双缝实验中，光穿过两条狭缝后射向远处的一个屏幕（一条缝在另一条缝的上方)。此时该屏幕上就出现明暗相间的条带。亮的条带是从一条狭缝射出的光波的波峰和波谷与来自另一条狭缝的光波的波峰和波谷分别发生相长迭加的地方，暗的条带则是发生相消干涉的地方，在这些地方，来自一条狭缝的光波波峰同来自另一条狭缝的光波波谷相互抵消。表述此概念的另一种方法是说亮的条带对应于屏幕上有较大可能被光子射到的地方，而暗的条带则是光子击中概率较低的地方。

根据量子力学法则。每当某一给定结果发生的可能途径为一个以上，且这些途径不何方法区别开来时，干涉就会发生。(这一干涉定义比教科书上通常提到的干涉定义更为一般。)在双缝实验中，光可以通过两种可能途径到达屏幕(即从上边一条狭缝或下边一条狭缝到达屏幕)，而且该实验没有用任何方法来确定哪些光子穿过哪条狭缝。如果我们能够以某种方式确定一个光子穿过哪条狭缝，就不会发生干涉，而这个光子最终可能射到屏幕上任何地方。其结果是条纹图案不会出现。简言之，没有两条不能彼此区分的路径，就不可能发生干涉。

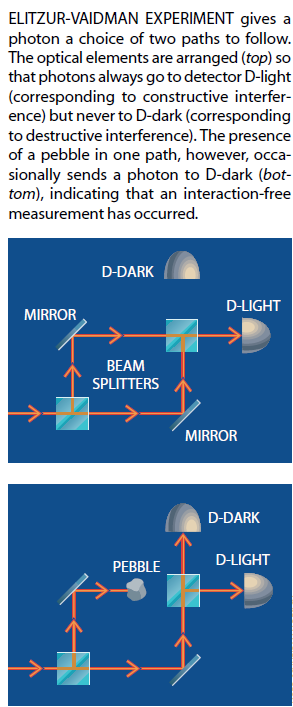
Elitzar和Vaidman开始时用干涉仪(由两块反射镜和两个分束镜构成的装置)来作为他们假想的测量系统的最初方案。进入干涉仪的光射在一个分束镜上，该分束镜使光沿着两条光路——上面一条和下面一条——行进。这两条光路在第二个分束镜上复合，此分束镜使光射向两个光子探测器中的一个。因此，干涉仪给每个光子提供了在光源和检测器之间行进的两条可能路径。

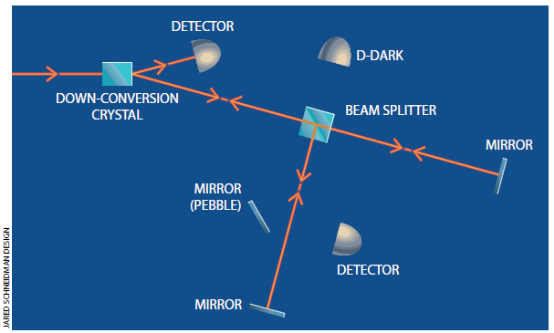
如果把穿过干涉仪的两条光路的长度调节到完全相等，那么这一方案实际上就变成了双缝实验装置。主要差别在于用光子探测器来代替显示亮暗条纹的屏幕。一台检测器被放置得使它只检测干涉图案中亮条纹的对应物(此检测器称为D亮检测器)。另一台检测器则记录暗条纹——换言之，没有光子到达该检测器(此检测器称为D暗检测器)。

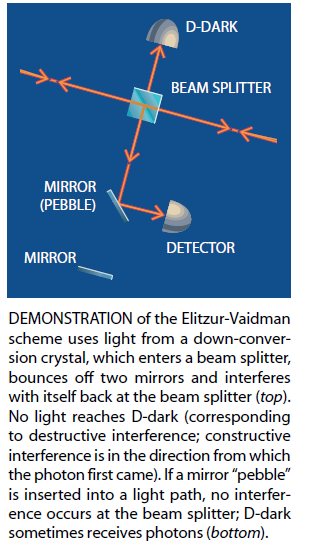
光路中的石子

如果一个石子被置于两条光路中的一条上(例如被置于上面一条光路)，那么会发生什么情况呢?如果第一个分束镜是随机分束的，那么光子将有50%的可能走上面一条光路并射在石子上(或引爆超级炸弹)，从而永远不会到达第二个分束镜。

  如果光子走下面一条光路，它就不会碰到石子。此外.由于光子只有一条路径可到达第二个分束镜，因此第二个分束镜上不再会出现干涉。这样，光子在第二个分束镜上就会作又一次随机选择。它可能被反射并射到D亮探测器上；这一结果不会提供任何信息，因为如果石子没有放在光路上这一结果本来反正也会发生的。但是光子也可以射到D暗探测器上。如果出现这个结果，我们就肯定地知道有一个东西在干涉仪的一条光路上，因为如果没有这个东西在那里，D-暗探测器是不可能被激发的。而且，由于我们只发出了一个光子，而它出现在D-暗探测器上，因此它不可能碰到石子。这样我们就得以进行了一次无相互作用的测量——我们确定了石子的存在，但没有同它发生相互作用。

虽然这一方案仅在部分时间内可行，但我们在此要强调指出，当这个方案可行的时候，它是彻底地可行的。这一成就背后的量子力学的魔力在于，任何东西—包括光在内——都有二重性，它们既是粒子又是波。当干涉仪内是空的时，光的行为就像波。它可以同时沿着两条路径到达检测器，这样就产生了干涉。当干涉仪内放人一颗石子时，光的行为就像不可分割的粒子，并仅循着一条路径行进。单是石子的存在就使得干涉不可能发生，尽管光子不需要同它发生相互作用。

为了证实Elitzur和Vaidman的设想，我们和Thomas Herzog(现在在日内瓦大学)两年前把他们的假想实验付诸实施，从而证明了无相互作用的器件是能够建造出来的。单光子源是一种特殊的非线性光学晶体。当来自一台激光器的紫外光子穿过此晶体时，有时它们会“降频变换”为两个频率较低的子代光子，这两个光子以大约30度的角彼此飞离。只要检测到其中一个光子，我们就有绝对把握确信其姐妹光子的存在。然后我们把这个光子引入我们的实验。

该光子进入了干涉仪，(为简单起见，我们使用的一种干涉仪与Elitzur和Vaidman所提出的稍有不同。)反射镜和分束镜的配置使得几乎所有的光子沿着进来的路径离开，(这相当于在Elitsur和Vaidman的例子中进入D-亮探测器，或者相当于在双缝实验中进入亮条纹。)在没有石子的情况下，由于相消干涉的缘故，光子进入D-暗探测器的可能性是微乎其微的（这种情况相当于双缝实验中的暗条纹)。

但是把一粒石子引入路径中就使情况发生了变化。这粒石子是一个使光线路径转向另一个探测器（D-石子探测器)的小镜子。于是我们发现，在大约一半的时间中，D-石子探测器记录到这个光子，而在大约四分之一的时间中D-暗探测器记录到光子。(其余的时间中光子沿着其进来的路径离开探测器，因而不提供任何信息。)D-暗探测器被激发就意味着不经过相互作用而检测到了石子。

我们对上述方案作了简单的推广，即降低了分束镜的反射率，从而使光子被反射到含有通向D-石子探测器的反射镜的那条路径的机会减小。我们发现，光子射到D-石子探测器和D-暗探测器的概率逐渐趋于相同，这一发现与理论预测符合。这就是说，使用稍有反射性的分束镜，在Elitaur一Vaidma方案中多达一半的测量可以是无相互作用的(光子循着进来的路径离开干涉仪的那些情况不算是测量)。

量子Zeno效应

立刻就出现了这样一个问题：百分之五十是我们能够取得的最佳结果吗?接着我们中间发生了许多争论(常常是激烈的争论)，因为不存在能够改进上述可能性的设计变动。然而1994年1月，斯坦福大学的Mark A. Kasevich到因斯布鲁克同我们会聚了一个月，在这一停留期间，他让我们了解到一种解决方案，此方案如能实现，就可以通过无相互作用的方式几乎百分之百地检测出物体。这并不是量子乐观主义战胜量子悲观主义的第一个例子(我们也希望它不是最后一个例子)。

新的方法多少采用了另一个奇异的量子现象。现在在布鲁塞尔大学的Baidyanath Misra和奥斯汀得克萨斯大学的E. C. George Sudarshan在1977年首次详细讨论了这一现象。一个量子系统基本上可以被限制在其初始状态中，虽然如果让它自行演变它将变到另外某种状态。之所以出现这种可能性，是由于测量能够对量子系统施加一种不同寻常的作用。这一现象称为量子Zeno效应，因为它类似于古希腊哲学家Zeno提出的著名悖论。Zeno否认飞行中的箭在运动的可能性，因为在它飞行的每一瞬间它似乎都是“冻结”了的。此现象又称“守候水壶等水开”效应，指的是那句“心急水偏不开”的谚语。我们都知道，守在水壶边等水开这一行动本身不应当(也的确不会)对烧开一壶水的时间产生任何影响。然而，在量子力学中，这样一种效应的确是存在的——测量的行动对结果有影响(这一原理称为“预测假设”)。

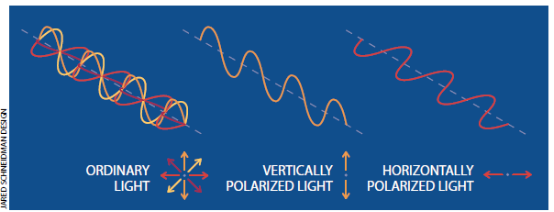
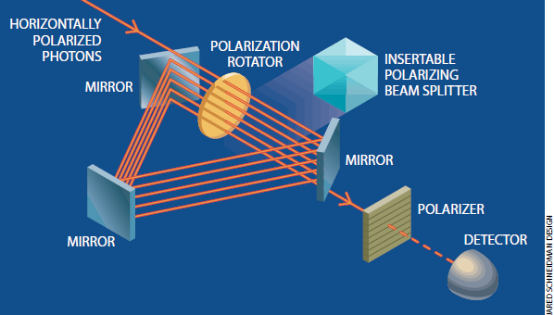
Kasevich实际上重新发明了这一效应的最简单的例子，它最初是在1980年由Technion-Israel理工学院的Ashei Peres提出的。这个例子利用了光的另一特性——偏振。偏振指的是光波振荡的方向—对于垂直偏振的光就是上下振荡，而对于水平偏振的光就是左右振荡。这些振荡方向与光的传播方向垂直.从太阳和其它典型光源发出的光通常在所有方向上振荡，但在本文中我们基本上只关心垂直偏振和水平偏振。

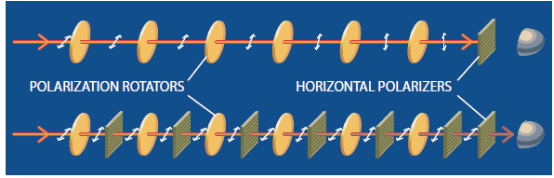
试考虑让一个光子穿过一系列(比如说6个)装置，其中每个装置都使光的偏振方向稍微转动一下，这样一个水平偏振的光子最终将变成垂直偏振的光子。这些偏振转动装置可以是含有比如说糖水的玻璃容器，在穿越这一系列偏振转动装置后，光子到达一个起偏器，此装置能够使具有某种偏振的光子透射过去，但却吸收在垂直方向上偏振的光子。在这个假想实验中，起偏器仅让水平偏振的光透射过去而到达检测器。

我们从一个水平偏振的光子开始。每一个偏振转动装置将使偏振方向转动l.5度。这样很明显，光子永远不会到达探测器，因为在穿过所有这些容器后它的偏振方向将转动90度(6个偏振转动装置，每个使偏振方向转动15度)，这样它就变成了垂直偏振光，而起偏器将吸收这个光子。偏振方向的这种逐步转动是我们想要加以抑制的量子演化过程。

这一抑制任务可通过在每一偏振转动装置后面放一个水平偏振起偏器来完成。其原因在于：光子经过第一个偏振转动装置后，它偏离水平偏振方向还不太远，这就意味着它被第一个水平偏振起偏器吸收的可能性是非常小的，仅为6.7%(从数学上看，这一概率由转动角的正弦的平方给出。)

如果该光子未被第一个起偏器吸收，那么它就再次处于水平偏振的状态——它必须处于这个状态，因为此状态是穿过水平偏振起偏器的光子唯一可能的状态。经过第二个偏振转动装置后，偏振方向又一次偏离水平偏振方向15度。在第二个起偏器上，光子又有同样小的可能性被吸收。如果未被吸收，它将再次以水平偏振的状态透射过第二个起偏器。这一过程将反复进行下去，直到光子到达最后一个起偏器。

一个入射光子有三分之二的可能性透射过所有6个插在其路径上的起偏器而到达探测器。这一概率由公式(cos2(15 0 ))‘给出。但是，随着我们增加转动级的数目，从而相应地减少每一级上的偏振转动角时(也就是用90度除以级的数目)，光子透射的概率也就增大。对于20个转动级，光子到达检测器的概率将近90%。如果我们能制造出一个有2500级的系统，则光子被某一起偏器吸收的可能性就只有千分之一。如果能有无限多级，则光子永远能穿过这一系统。这样，我们就将完全抑制转动的发展。

为了实现量子Zeno效应，我们使用先前用过的非线性晶体来制备单个光子。我们不用6个偏振转动装置和6个起偏器，而是只各用一个。为了达到同样的效果，我们用3块反射镜来形成一种螺旋形的阶梯，从而使光子穿过偏振转动装置和起偏器6次。在没有起偏器时，我们发现光子离开阶梯时总是垂直偏振的。而在有起偏器时，我们发现光子是水平偏振的(除非起偏器挡住了它)。对于我们这个6次循环的实验，这些情况发生的可能性大约为三分之二，正如我们对假想实验的分析所预期的那样。

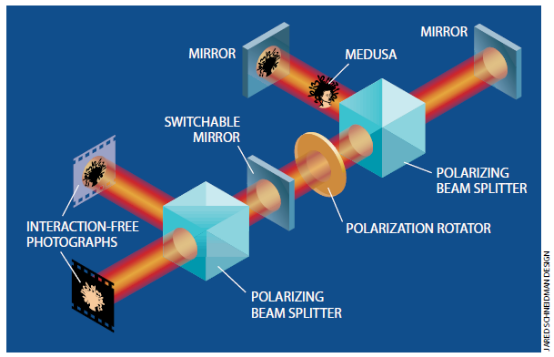
接着我们着手进行一次高效的无相互作用的测量——也就是说，检测一个不透明物体而同时不让任何光子射到这个物体上。我们设计了一个系统，它有点像是Zeno的例子和原始的Elitsur-Vaidman方法的混合物。一个水平偏振的光子入此系统并在系统中转了几圈(比如说还是6圈)后离开系统。(为此，需要有一个能够极为迅速地“开关”的镜子。幸运的是，这种镜子——实际上是可开关的干涉器件——已经为激光脉冲研制出来了。)在此系统的一端上是一个偏振方向转动装置，它使光子的偏振方向在每一周期中转动15度。另一端则有一个偏振干涉仪，它有一个起偏振分束镜和两条等长的干涉臂，其端点是反射镜。

在起偏振分束镜处，所有水平偏振的光都透射过去。而所有垂直偏振的光都被反射。实际上，透射和反射的选择类似于双缝实验中的两条路径。在偏振干涉仪中没有放置物体时，光就在偏振分束镜上根据其极化方向分为两束，分别被每一干涉臂端点处的反射镜反射后又在分束镜上复合。其结果是光子的状态与它进入干涉仪之前的状态完全相同(也就是说其极化方向向着垂直方向偏转了15度)。这样，经过6次循环后，偏振方向最终转到垂直方向上。

当一个不透明物体放人干涉仪的垂直偏振臂上时，情况就发生了变化。这种情况类似于在量子Zeno效应实验中放人8个起偏器。这样，在第一个周期中，光子——它的偏振方向从水平方向上仅偏转15度——进入垂直偏振臂以而被这个物体吸收)的可能性是极小的(同Zeno假想实验一样为6.7% )。如果未发生吸收，则光子必定进入了水平臂，而它的极化方向也就回复到完全水平的方向上。

正如Zeno的例子一样，这整个过程在每一周期中重复一次，直到经过6个周期后，底端的反射镜关掉，光子就离开了系统。在测量光子的偏振方向时，我们发现它仍是水平的，这意味着育一个阻挡物必定在干涉仪中。否则，光子在离开系统时已成为垂直偏振的。此外，通过增加周期，我们可以使光子被物体吸收的概率减小到我们希望的任意小的程度。在洛斯阿拉莫斯国家实验室进行的新实验的初步结果已证明，有多达70%的测量可以是无相互作用的。我们很快就希望把这个数字提高到85%。

运用量子魔术

所有这些量子魔术有什么用处呢?我们觉得，现在的情况有点类似激光器出现的最初几年那样，当时科学家们知道激光器是许多未知问题的理想解决方案。无相互作用测量的新方法可以用来比如说作为一种很不寻常的照相方法，在不让一个物体接触光线的情况下把它摄下来。

这种“照相”过程可按下述方式进行：我们不是送入一个光子，而是送入许多个光子(每个像素一个光子)，并用这些光子进行无相互作用的测量。在没有物体阻挡干涉仪光路的那些区域中，光子的水平偏振将如所预期那样逐步向垂直方向转动。而在有物体阻挡干涉仪光路的那些区域，一些光子将被吸收，剩下的光子的偏振则被限制于水平状态。最后，在光子完成了规定数目的周期后，我们将通过一个偏振滤光器摄下光子的一幅照片。

如果滤光器是被水平地装定的，我们就得到物体的一幅图像；如果它是垂直装定的，我们就得到负片。在任何情况下，图像都是由从未碰到过物体的光子构成的。这类方法也适用于半透明的物体。而且或许还能进一步推广以发现物体的颜色(不过这些目标将是更难实现的)。

这类成像方法的一个变种有朝一日可以设想在医学中具有很大价值——比如说作为一种使活细胞成像的方法。想象一下我们能够在不让某人多次受X光照射的情况下对其拍X光片。这类成像方法与常规X光技术相比，患者所冒的风险较小。(实际上，考虑到难于制得这一波长的光的光学元件，这类X光摄影术是不大可能实现的。)

一种更直接的候选用途是对最近在各个实验室产生的超冷原子云成像。这些原子云中最冷的原子云显示玻色-爱因斯坦凝聚；这是一种新的量子状态，在这一状态中，许多原子合起来显示一个实体的行为。在这样一种原子云中，每一个原子都是极冷的—也就是运动得非常之慢—以致单单一个光子就可以把原子撞出原子云中。以前不存在一种可以获得凝聚态的图像而同时又不破坏原子云的方法。无相互作用的测量方法可能是使这样的原子集合成像的一条途径。

除了使量子物体成像以外，无相互作用的方法也可以制造某些类型的量子物体：也就是说，这些方法可以扩大“薛定谔的猫”——量子力学中的一个深受人们喜爱的理论实体——之类量子物体的创造范围。这只量子猫被创造为同时存在于两种状态中：它同时既是死的又是活的，即两种状态的迭加。1996年早些时候，美国国家标准与技术研究所的研究人员设法用一个铁离子创造了一种初级形态的薛定格的猫——一只“小猫”。他们通过激光器和电磁场的联合使用，使这个离子同时存在于相距83纳米的两个地方（在量子尺度上83纳米是一个巨大的距离)。

如果用无相互作用的方法来询问这样一个离子，则询问光子也将处于迭加中。它最终可能同时是水平偏振和垂直偏振的。实际上，前面所讨论的那类实验方案应当能够使一组光子(比如说20个光子)处于相同的迭加中。每个光子都“知道”它的偏振方向与其它所有光子的偏振方向相同，但任何一个光子都不知道它自己的偏振方向。这些光子将保持在这一迭加态中，直至测量显示出它们全部是水平偏振的或垂直偏振的。这样一大群光子保持在这一特殊的状态将说明量子效应可以在宏观尺度上展示。

无相互作用测量的概念超出了日常生活经验的范围，它似乎是极为怪异的，如果说还不是彻头彻尾的谬论的话。如果人们记住，量子力学是在“潜在可能”这一领域中起作用，那么或许会觉得它不那么怪。我们能够防止一种相互作用发生，正是因为本来可能会出现相互作用。

如果这样还无济于事，那么下面这一事实可以给人一丝安慰——多年来，甚至连物理学家也曾觉得难以接受量子世界的奇异性。这些量子魔术的根本关键——光的互补的波——粒子性质和量子测量的本性——自1930年以来就已经被知道了；物理学家们只是到最近才开始应用这些概念来提出量子信息处理中的新现象，包括在黑暗中窥看的能力。

预测原理

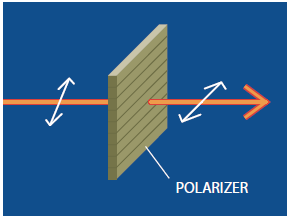
这个原理是说对一个量子系统进行的任何测量，都只能得到某些可能的答案。而且，在进行测量之后，量子系统就处于由获得的结果所确定的一个状态中。因此，一个光子在穿过了水平起偏器以后，必定是水平偏振的。即使它最初是在一个近于垂直的方向上偏振(起偏器消除了垂直偏振分量)。不过，在这种情况下光子透射过起偏器的概率是比较低的。