互动科普

在一些新材料中，数十亿个电子之间形成了极其复杂的量子纠缠态。物理学家发现，可以借用看似与之毫不相干的弦论思想，来解决这个极为棘手的问题。

撰文：苏比尔 · 萨契戴夫（Subir Sachdev） 翻译：庞玮

研究对象的差别反映出了研究主旨的不同，弦论学家极负盛名，在我赴会时，深知他们炉火纯青的数学技能。我曾花了几个月的时间去阅读弦论学家们的论文和著作，结果是自取其辱，我想自己肯定会被当成一个无知的新手而饱受白眼。不过，弦论学家理解起一些凝聚态物理中最简单的概念时，也困难重重，所以我不得不画一些给刚入学的研究生上课时才会用到的图释，来帮助弦论学家们理解。

那我为什么还要参加这个弦论大会呢？最近几年，很多和我一样研究凝聚态物质的专家都发现，我们研究的对象会出现一些超乎想象的行为，它们能形成非常特殊的量子相（quantum phases），这种物态结构与自然界中一些最奇怪的现象有关。1935年，阿尔伯特·爱因斯坦、鲍里斯·波多尔斯基（Boris Podolsky）和内森·罗森（Nathan Rosen）发表了一篇著名的论文（文献中往往取三人姓氏首字母称之为EPR论文），让物理学家注意到，在量子理论中，粒子（比如电子）之间存在一种“幽灵般”的联系，我们现在称之为量子纠缠（quantum entanglement）。

处于量子纠缠的两个粒子（比如电子），在没有直接物理作用相联系的情况下，也能产生关联。EPR论文中考虑的是一对电子，但在金属和超导体中包含大量电子，一块标准的实验样本材料所含有的电子数量约为1023个，而在某些材料中，情况则复杂得令人发指。

我的大部分研究生涯都在跟这些东西进行脑力角斗，这不仅仅是个学术问题：超导体正逐渐成为非常重要的应用技术，因此物理学家不得不更加努力地去弄清它们的性质和性能。

我和同事逐渐认识到，弦论能对上述问题提供一个前所未有的解决之道。在寻求统一基本粒子和爱因斯坦引力理论的过程中，弦论学家偶然发现了“对偶性”（duality）——不同物理领域之间隐藏的内在联系。对偶能将量子效应弱、引力作用强的理论和量子效应强而引力作用弱的理论联系起来，因此利用这种对偶性，我们能将对某一个领域的理解，应用于另一个领域。这意味着我们同样能将纠缠问题转变成一个引力问题，然后借用弦论学者为研究黑洞所建立的方法，解决纠缠问题。正所谓他山之石，可以攻玉。

材料如何导电？

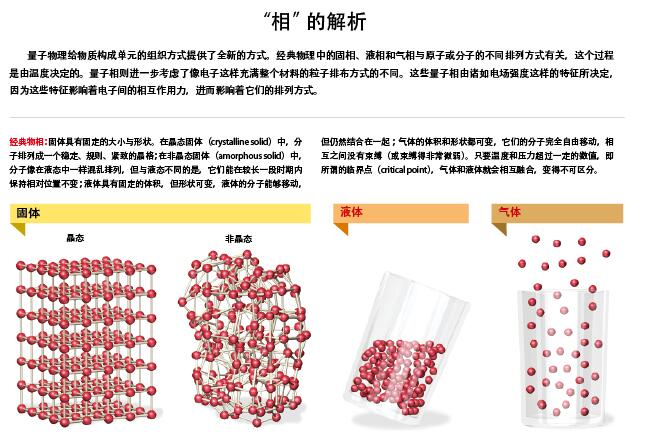
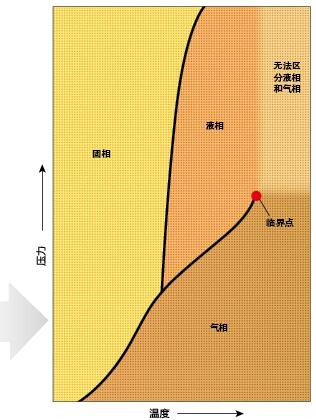
为了理解以上观点，让我们先回顾一下高中物理。高中老师告诉我们，物质分成固、气、液三相。我们凭借直觉就能掌握这三种相的区别，固体具有固定的大小和形状；液体则随容器附形；气体与液体类似，但它们的体积改变起来更容易。尽管这些区别非常明显，但直到20世纪初，科学家才对物质的相有了一个完整的科学描述。现在我们知道，三种相的区别在于，晶态固体中原子排列规则、紧密；而液体和气体中的原子自由松散。

但是，这三种相并不是物态的所有可能表现形式。固体不光只是一团原子的排列，而且还包含不计其数的电子，每个原子都会贡献出一些电子，这些电子在整个晶体中四散漫游。当我们在一块固体样品两端加上电压时，这些电子就顺势流动形成电流。原则上，所有材料都服从欧姆定律：电流等于电压除以材料的电阻。像特氟隆（teflon，即聚四氟乙稀）这样的电绝缘体（Electrical insulator），只不过是具有很高的电阻而已，而铜这样的导电金属则具有较低的电阻，最特殊的还是超导体（superconductor），它的电阻几乎为0.1911年，海克·卡默林·昂内斯（Heike Kamerlingh Onnes）在把固态水银冷却到-269℃时，发现水银变成了超导体。今天我们知道，还有些超导体的要求相对不那么严苛，在-138℃时就会进入超导状态。

尽管不如气、固、液三相的区别那么直观，导体、绝缘体和超导体也属于不同的物相，在这三种相中，电子群具有不同的形态。过去20年间，物理学家在固体中发现了更多的电子相（phase of electron），其中特别吸引人的一个，甚至连个正式的名称都没有，物理学家通常叫它奇异金属（strange metal），因为它的电阻随温度变化的方式与一般金属完全不同。

这些电子相的区别是由电子集体行为的差异造成的。在固体、液体和气体中，原子的运动可以用经典的牛顿力学来描述，但要描述电子的行为不可避免地涉及量子理论。主导固体中电子行为的关键量子物理法则，与原子内部电子服从的规律一样，只不过是其放大版本而已。对一个围绕在原子核外的电子，量子物理用一列绕核传递的波来描述其运动，这个电子可处的状态有无限多个，我们可以通过一些特定的可观测属性（observable properties）来区分，比如说不同状态具有不同能量。更为重要的是，电子不仅在绕核运动，而且还在绕着自身的“转轴”自旋（spin），这种自旋要么顺时针要么逆时针，且速度永远恒定，通常我们用“向上”（up）和“向下”（down）来标记这两种自旋状态。

如果原子有多个核外电子，这些电子必须要遵守一个最重要的规则：泡利不相容原理（Pauli exclusion principle），即没有任何两个电子能占据同一个电子态（该原理适用于所有物质粒子，物理学家称这些粒子为费米子）。如果你往原子中不断加入电子，每个新加入的电子都会尽量处于所能允许的能量最低状态，就像水从瓶底慢慢向上灌满整个瓶子一样。

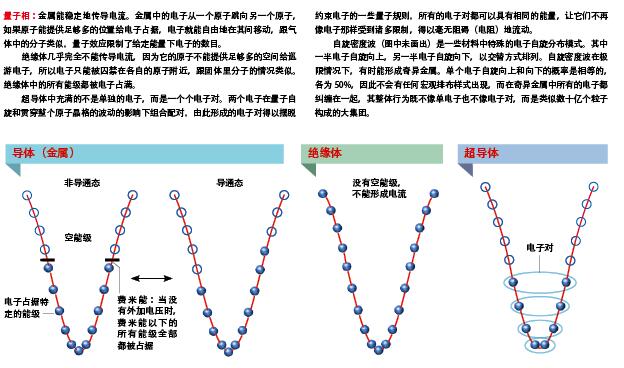
对于一块含有1023个电子的金属，上述原则也同样适用。一旦脱离原子的束缚，电子就成为巡游电子，占据那些扩展至整个晶格结构的状态，这些状态可以类比成一个个正弦波，不同的波长对应不同的能量，电子在泡利不相容原理允许的范围内，依次占据能量最低的那一个状态，最终所有的、能量低于某个阈值的状态都被电子填充，这个阈值被称为费米能（Fermi energy）。

现在，如果给这块金属两端加上一个电压，某些电子就能获得足够的能量，从已占据的能态迁移到一个费米能之上的未占据能态（见图“物质的态”），然后这些电子就能在金属中自由移动，从而形成电流了。而在绝缘体中，电子密度导致所有可能的状态都被完全占据，此时即使我们加上一个电压，电子也无处可以迁移，因此就无法形成电流。

在超导体中，情况变得更为复杂。超导体中的电子不能被视为一个个单独的电子，而是两两组合的电子对。1957年，理论物理学家约翰·巴丁（John Bardeen）、莱昂·库伯（Leon Cooper）和罗伯特·施里弗（Robert Schrieffer）发展出了一套理论（通常被称为BCS理论），首次描述了这种配对。表面上看起来，电子的这种组合似乎不合情理，因为两个电子会相互排斥，但是，原子晶格的振动会间接产生一种吸引力，能够克服电子间的排斥作用。电子配对之后，每个电子对的行为就不再像一个费米子，而像一个玻色子，玻色子是另一种量子粒子，它们不服从泡利不相容原理，因此这些电子对现在可以全部挤进能量最低的那个状态，形成所谓的玻色－爱因斯坦凝聚（Bose- Einstein condensation）。这就好比你往瓶子里灌水，水位不是越来越高，而是在瓶底形成了一层薄薄的冰层，无论你灌进多少水，都会被这层冰吸收，而且它的厚度还不会增加。

如果你给这种材料的两端加上电压，电子对就会在电压的驱动下，进入一个能量比最低能态稍高一点的状态，并形成电流。随着电流的流动，这个稍高的能态又被空出来，因此后面的电子对便可以毫无阻碍地持续进入这个状态，正是基于这种方式，电流在超导体中流动时才完全没有阻碍。

量子临界点

量子理论如此成功地解释了金属、绝缘体、超导体以及半导体材料（semiconductor）的性质，使得20世纪80年代初的物理学家认为，对固体中电子行为的完整描述就要大功告成了，不会再有什么重要发现了。但这种自信很快就被高温超导体的发现一扫而光。

其中一个例子就是砷化铁钡（barium iron arsenide），实验物理学家将砷化铁钡中的一部分砷替换成磷，得到的新化合物在低温下是超导体。物理学家相信其背后的理论机制与BCS相似，只是电子间的吸引力不是来自原子晶格的振动，而是与电子自旋相关的物理性质有关。

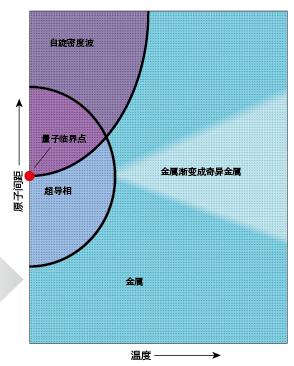
由于掺进了一小部分磷，材料中形成了所谓的自旋密度波（spin–density wave）。在一半的铁原子基团中，电子自旋更倾向于向上而不是向下，而在另一半铁原子基团中情况刚好相反，随着磷原子数目的增加，自旋密度波的强度越来越小，如果被替代的砷超过一个临界比例，大约30%，自旋密度波就会完全消失，此时，电子自旋在每个基团中向上和向下的概率又重新相等，我们可以由此得到一些重要的结论。

当实验物理学家将磷含量的比例固定在30%并升高温度时，这种量子临界状态的神秘本质开始初露端倪——我们得到的既不是超导体，也没有自旋密度波，而是一种奇异的金属（strange metal）。

为了描述这个量子临界点（quantum-critical point）及其附近的超导相和奇异金属相，我们要借助的最主要的工具，正是量子力学中那个让爱因斯坦、波多尔斯基和罗森深感不安的性质：纠缠。

前面已经提到过，纠缠是两个状态的叠加，例如这个电子自旋向上，那个电子自旋就向下，反过来也是一样，不同铁原子基团中的两个电子之间就是这种叠加状态。原则上电子是不可区分的，因此我们没法具体说哪个电子自旋向上，哪个自旋向下，电子自旋向上和向下的概率都是50%，我们只能说如果测量出这个电子自旋向上，那么另一个电子自旋一定是向下的，它们处在完美的反关联（anticorrelated）状态，只要知道其中一个，另外一个也就确定了。

乍看上去，纠缠可能并不值得我们讶异，反关联在我们生活中很常见：如果你有一双鞋，一只放在前门过道里，另一只放在后窗阳台上，然后你发现过道里的是左脚那只，那阳台上那只就肯定是右脚上的，这有什么奇怪的呢？但是这与量子纠缠存在本质上的不同，一只鞋，你不去看它，也知道非左即右，但是一个电子，在人们没有对其测量之前，是不能确定其自旋的（我们可以通过一些特定测量来确定电子的自旋）。或者可以说，除非面临非此即彼的选择（比如说被测量），单个电子的自旋同时处在向上和向下的叠加状态。

让人难以理解的地方在于，纠缠电子对是如何保持这种反关联的，只要一个电子做出选择，另一个也同时做出选择，它们怎么知道要选择与另一个刚好相反的自旋呢？似乎原子2瞬间就知晓了原子1的量子态信息，完全不管它们之间相隔的距离有多远。事实上，处于纠缠状态中的两个粒子，并没有属于自己单独的量子态，只有这对粒子共同的量子态，这就是所谓非局域性（nonlocality），一种远距幽灵般的作用，爱因斯坦为此深感不快。

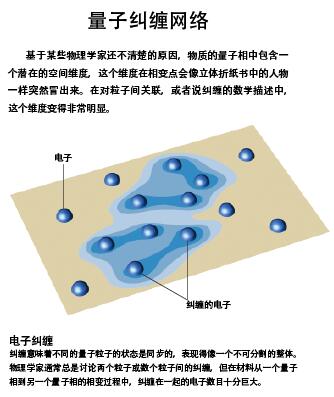
不管你是否赞同非局域性，非局域性已经在众多实验中得到了验证，爱因斯坦及其合作者显然触及的是量子力学中最违反直觉、最出人意料的一面。在过去10年里，物理学家开始领会到，非局域性正是奇异金属古怪性质的来源。在量子临界点附近，电子的行为不再独立或两两配对，而是集体纠缠在一起。EPR论文中关于两个电子纠缠的思路，同样适用于1023个电子，相邻的电子两两纠缠在一起，每个纠缠电子对又和临近的纠缠电子对进一步纠缠，如此反复，形成了一个巨大的内部相互作用网络。

其他材料中也有同样的现象，对这些纠缠态进行分类、描述，是我们在发展用以描述这些新材料的理论过程中，面临的严峻挑战。这个相互作用网络过于复杂，目前我们还不能对其进行直接描述。

在我们了解到弦论之前，我和同事曾担心，可能永远也找不到一个能描述这些量子物相的理论。

“额外维”里的电子纠缠

表面看上去，弦论跟多个电子之间的纠缠态毫无联系，弦论关心的是一些微观的弦，这些弦像小型吉他弦那样不停地振动，不同的振动模式代表不同的基本粒子。物质的弦本质在极高能量下才会显现出来，如此高的能量只存在于宇宙大爆炸之初或非常致密的黑洞附近。

20世纪90年代中期，美国加利福尼亚大学圣巴巴拉分校卡弗里理论物理研究所的约瑟夫·波尔金斯基（Joseph Polchinski）意识到，弦论不仅预言了弦，还暗示“膜”（brane）的存在，弦就像毛巾上的绒毛一样附着在这些膜上，而这些膜则代表了一个全新的物理领域，超出了高能粒子这一弦论设计之初的研究目标。

我们所认为的点粒子，也许实际上是从更高维空间的膜上伸展出来的一根弦的末端，我们既可以将这个宇宙看成，由在四维时空中运动、彼此之间存在复杂相互作用的点粒子构成，也可以将宇宙看作由附着在膜上、在五维时空中抖动的弦构成，这两种描述其实是等价的（也就是对偶的），而且还可以互相弥补各自的缺陷：当我们用点粒子观点去描述某个问题而显得过于复杂时，用弦论也许更为简单；反过来，在某些用点粒子可以描述得一清二楚的问题上，弦论则可能显得臃肿笨拙。

对我而言，弦在更高维时空中的物理图像并不重要，甚至在极高能量下，弦论能否正确解释粒子物理学也与我无关。我所关心的是，上述对偶性让我得以将一个数学上的棘手问题，改头换面成一个容易解决的形式。

几年之前，我参加的还主要是凝聚态物理的会议，当时大家对新发现晶体中电子可能形成的不同量子纠缠态争论不休，而现在我正和弦论学家一起品着咖啡，努力理解他们对弦和膜抽象又晦涩的描述，并琢磨着如何让这些奇异的想法降落凡尘，用它们来解决实验桌上那些新材料中的问题。不仅如此，这种交流也可以互通有无，我想我们对电子量子相的直觉和实验经验，对弦论学家描述黑洞和其他怪异对象也不无裨益。

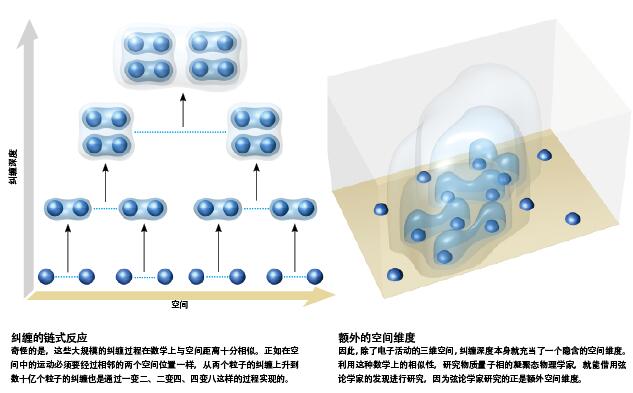
当晶格中的电子仅有有限的纠缠自由度时，我们可以认为这些电子是粒子（最初的电子或电子对）。当大量电子之间出现很强的纠缠时，这些电子就不能看做是粒子了，传统的理论方法已经难以描述它们的行为了。而在新的方法中，我们则用弦在额外空间维中传播，来描述这些系统。

我的哈佛大学的同事布里安·斯温格尔（Brian Swingle）画了一幅图，展示了量子纠缠网络和额外空间维度之间的相似性（见图“与弦论相关”）。在量子纠缠网络中，粒子向上和向下移动，在数学上正好类似于在空间中的运动。弦可以在额外空间维度中扭摆、合并，而这正好与粒子间纠缠的演化相对应。简而言之，只要你将纠缠自由度类比成额外空间维度中的距离，困扰爱因斯坦的那种粒子间幽灵般的联系就不再是一团乱麻了。

从超流体到绝缘体

对偶性的实际好处在于，弦论学家为了解决从大爆炸熔炉中的粒子动力学到黑洞边缘量子场的起伏等各种问题，早就准备好了一个庞大的数学宝库，我们这些研究量子物相的专家只要走进宝库，找到某个特定问题的可能解决方法，然后把它从弦论问题转变（利用数学上的对偶性）成纠缠问题就可以了。

我们通常关注的是在绝对零度处的最低能态，不过通过一种看上去颇为戏剧化的手段，我们也能逐步描述非绝对零度下的物态，那就是先想象在弦论情形中如何引入一个黑洞。研究物态竟然要动用黑洞，这表明上述对偶性十分不同寻常，当然我们不是说量子物态真的含有黑洞，它们之间的联系要更加微妙。剑桥大学的霍金有过一个重要的发现：每个黑洞都有一定的温度，从外部看来，黑洞就像是一块烧红的炽热煤炭。按照对偶性来推测，相对应的凝聚态系统肯定也是热的，正是这种效应将自旋密度波或超导体变成了奇异金属。

这些方法在解释奇异金属和其他物态方面已经取得了一些进展，但它们最具价值的地方还在于，能够描述超流体（superfulid）到绝缘体的转变。超流非常类似于超导，只不过它是由电中性原子形成的，除了具有零电阻之外，超流还具备另一种特性，即能够毫无黏滞地流动。最近几年，实验物理学家用一些令人惊叹的新方法，制造出了人工超流体。他们用激光束交织出一个晶格结构，然后加入数十亿个超冷原子，这些原子一开始表现得像超流体，能够无阻碍地从一个晶格点流向另一个晶格点，但随着实验人员逐渐增加激光束的强度，原子的流动性变得越来越差，然后就突然从超流状态转变成绝缘体（即原子被束缚在各个晶格点，完全不能在晶格点间迁移）。

为了追踪超流体到绝缘体的相变过程，实验物理学家测量了原子在外加压力下的流动。在超流相中，原子毫无阻碍地流动；在绝缘体相中，原子基本上完全不能流动；而在两相分野的相变点，原子则以一种特殊的方式流动。比如在其中一项测量中，实验人员撤销了外加的扰动，这些原子便逐渐停止了流动，停止速度的快慢则取决于温度和普朗克常数（量子理论中的一个基本参数），在其他非量子物相中是不会出现普朗克常数的。为此，我们设想了一种可以与黑洞形成对偶的量子临界流体（quantum-critical fluid），对上述现象做出了解释。

对偶性也并非无往不利。本质上，这种方法能化繁为简，但我们并不总是想投机取巧，我们同样需要理解量子纠缠网络的复杂性。对偶性就像数学上的一个黑盒子（blackbox），使得我们几乎对复杂纠缠态的细节，以及它在实际材料中的产生过程一无所知，因此要解释材料中究竟发生了什么还为时尚早。对于我们这些习惯在晶体中思考电子动力学行为的凝聚态物理学家而言，弦论赋予我们一种全新的视角，去观察了解包含复杂纠缠量子态的动力学演化过程。而对弦论学家来说，对偶性能引起他们对量子材料物相的兴趣，这也不失为在早期宇宙或高能物理加速器研究上的一种有益调剂。两种思维交汇所带来的奇妙影响，显示出大自然浑然一体的美丽和谐。