互动科普

游客困境

露西和皮特跑到太平洋一座偏远的小岛上游玩，各买了一件一模一样的古董。不料，航空公司把他们托运的这两个宝贝弄坏了。面对两位乘客的兴师问罪，公司经理爽快地答应赔偿，但这两个古怪的东西究竟价值多少，他一点头绪也没有。经理寻思，如果直接向两位乘客询问，根本就是自讨苦吃，因为他们肯定会狮子大开口，报一个天价。

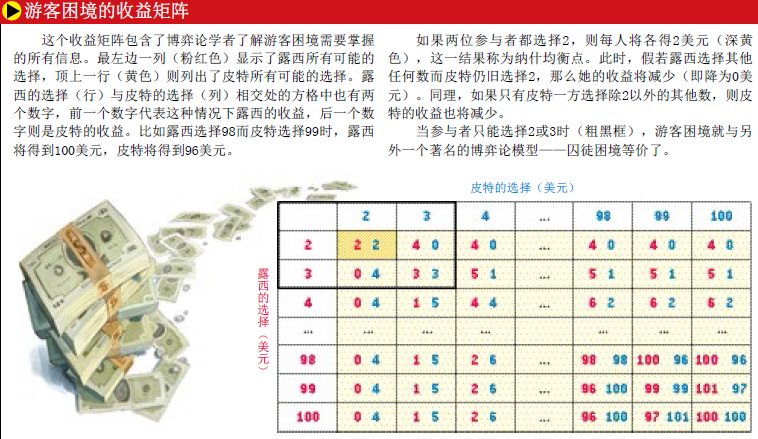
于是经理脑子一转，想出了狡猾的一招。为了不让这两位乘客有机会统一口径，他要他们分别写下古董值多少美元，且此价格必须为2到100之间的一个整数。如果两人写出的价格相同，经理将认为这的确是古董真正的价格，并按此数额赔偿两位乘客。如果两人写出的价格不同，经理将认为较低的那个价格才是古董真正的价格，而报价较高的那位乘客显然是在说谎。在这种情况下，经理将按较低的价格赔偿，同时给报价较低的那位乘客另加两美元以奖励他的诚实，而对报价较高的那位乘客则扣除两美元作为惩罚。如果，露西写出的价格是46美元，而皮特写出的是100美元，那么露西将获赔48美元，而皮特只能得到44美元。

露西和皮特会报出多高的价格？如果是你，又会写出一个多大的数字呢？

在假想的这一幕中，某个或某些人需要作出选择，这些选择将决定他们的收益。研究这类问题的学者被称为博弈论学者，而这类问题则被他们称为博弈或赛局。这个赛局是我在1994年构想出来的，我称之为“游客困境”（Traveler’s Dilemma，缩写为TD）。设计这个赛局的目的，是要驳斥经济学家和许多政治学家对合理行为及认知过程所持有的狭隘观点，质疑传统经济学的自由主义观点，同时凸显“合理性”在逻辑上的矛盾。

“游客困境”实现了这些目标。我们对这个赛局进行一番逻辑推理后就会发现，最合理的选择应该是２美元，但无论是根本没有进行逻辑思考而凭直觉选择的人，还是完全意识到自己的选择已远远偏离“合理”值的人，都会不约而同地倾向于选择100美元。此外，赛局的参与者不按常理行事反而会获得更大收益，看来，在TD博弈中，不照“合理”规则出牌倒是一种比较合理的做法。

在我构想出TD赛局之后的10多年中，它已经逐步发展为一个独立的研究课题。众多学者进一步发展了TD概念，并报道了若干实验结果。这些研究加深了我们对人的决策过程的认识，但如何把逻辑与推理应用于TD，这个问题依然悬而未决。

博弈，不走寻常路

为什么2是合乎逻辑的选择呢? 我们可以考虑下面这条似乎无懈可击的思路。拿露西来说，她的第一个念头就是赶快写下最大的数（100）。如果皮特也同她一样的话，那她铁定就有100美元到手了（假若古董的价格远低于100美元，那么露西此刻必定在偷着乐了：遇上航空公司经理这等大傻瓜，想不发财都难）。

然而转念一想，露西立刻发觉99更加合理——她说不定还能多得1美元，即获赔101美元。不过皮特肯定也有同样的想法。如果两人都写99，露西将得到99美元。如果皮特写了99，那么对露西来说，更明智的选择是98，这样她还是能捞到100美元。但皮特的思路肯定与她不谋而合，他也会写98的。于是，露西再次改变念头，觉得该写97，弄到99美元也不错。以此类推，露西和皮特选择的数字就会越来越小，最终两人都会选择那个最小的数——2。当然，在现实生活中，像露西这样跟皮特竞相杀价，一直到2才肯罢休的事情，几乎不可能发生。不过没有关系，这是逻辑推理得出的“合理”结论（实际上却大有关系，甚至可以说是整个问题的关键所在）。

上面这种分析思路被称为反向归纳（backward induction，又称倒推法），是博弈论学者广泛应用的一种分析方法。按照反向归纳法的预测，每位参与者写下的数都是2，因此最终将各得两美元（难怪那位航空公司经理的事业会如此一帆风顺了）。实际上，博弈论学者使用的几乎所有模型，对TD赛局的预测都是这样一个结果——两位参与者绞尽脑汁反复算计，总想着小一点的数会对自己更有好处，到头来反而比不假思索写个100少赚了98美元，这正应了聪明反被聪明误的老话。

“游客困境”同另一个知名度更高的经典博弈论模型——“囚徒困境”（Prisoner’s Dilemma）有关。两名嫌疑犯因犯下一桩重罪而被逮捕，并被分开审讯。摆在他们面前的有两条路：一是揭发对方（从而换取从轻处罚），二是保持沉默（在这种情况下，如果对方也保持沉默，警方就缺乏足够的证据了）。乍听起来，这似乎与两位游客古董受损的故事截然不同，但如果把TD赛局中每位参与者的选择范围，由2到100改为只能在2和3中选一的话，从数学的角度看，囚徒困境中每种选择的收益就跟TD赛局完全相同了。

博弈论学者分析博弈模型的方法，是抛开那些有声有色的故事情节，直接抓住最本质的东西，也就是所谓的收益矩阵（payoff matrix）。收益矩阵是一个方阵，包含了与每位参与者可能的选择及所得收益相关的全部信息（参见第73页图表）。露西的每一种选择对应于收益矩阵的一行，而皮特的选择对应于收益矩阵的一列。所选方格中的两个数分别代表他们各自的收益。

虽然囚徒困境和只有两个选项的游客困境都名为“困境”，但它们并未将参与者置于真正的进退两难、无所适从的境地。每位参与者都会发现，他们只有一种毫不含糊的正确选择，那就是2（对于囚徒困境这个故事来说，正确选择就是揭发对方）。这一选项被称为支配选择（dominant choice），因为无论对方怎么出招，选2都不会处于下风。如果露西选择了2，那么当皮特选3时，她就可以拿到4美元（此时露西如果选3，就只能拿到3美元了）；当皮特也选2时，她还是可以拿到2美元。

相反，完全版本的游客困境（即选项为2到100的TD）则不存在支配选择。如果皮特选2或选3，那么露西自然选2最好。但如果皮特选择4到100之间的任何一个数，那么对露西来说，上策是选一个比2更大的数。

在研究收益矩阵时，博弈论学者常常要用到纳什均衡（Nash equilibrium），这是以美国普林斯顿大学数学家小约翰·福布斯·纳什（John F. Nash, Jr.）的名字命名的[演员罗素·克罗（Russell Crowe）在奥斯卡获奖影片《美丽心灵》（A Beautiful Mind）中塑造了纳什的形象〕。纳什均衡指的是这样一种结果，即对局的双方不可能通过单方面改变选择而获得更好的收益。试看，TD模型中（100，100）这个结果，前一个数字是露西的选择，后一个数字是皮特的选择。如果露西改变主意而选了99，那么结果就变成了（99，100），这样她将得到101美元。露西的改变使她自己占了便宜，因此（100，100）这一结果不是纳什均衡点。

TD只有一个纳什均衡点——（2，2），此时露西与皮特均选择2。纳什均衡的应用非常广泛，这也是为数众多的分析方法不约而同地预言，该结果是TD对弈最佳结果的主要原因。

博弈论学者还提出了其他一些平衡概念，诸如严格均衡（strict equilibrium）、理性方案（rationalizable solution）、理想均衡（perfect equilibrium）、强均衡（strong equilibrium）等等，但所有这些方案应用到TD模型时，给出的都是（2，2）的预测。问题恰恰就出在这里：大多数人肯定会觉得自己将选一个比2大得多的数，从而获得远远超过2美元的收益。我们的直觉看来与博弈论的预测完全是背道而驰的。

挑战传统经济学

TD模型以及我们对该模型对弈结果的直觉预测，也同经济学家的理念相冲突。早期经济学家牢牢立足于自由主义的观点，主张放手发挥个人的积极性而不加干预，因为他们认为个人的利己选择汇合在一起，将会促使经济高效运行。博弈论方法的兴起，已经在很大程度上帮助经济学摆脱了这种观点的影响。但长期以来，博弈论方法都是建立在一个公认的原则之上，即人们将作出有利于自己的理性选择，而且这一选择是博弈论能够预测的。自由主义经济学的观点认为，不加约束的利己动机有利于提高经济效率，而博弈论主张人既是自私的又是有理性的，TD模型则左右开弓，把这两个观点全都推翻了。

在TD模型中，“效率”最高的结果是两位参与者都选择100，只有这样他们才能获得最大的总收益。然而，自由主义的利已动机却要求，参与者为了个人能够获得更多收益而抛弃100这个最佳值，转而选择其他较低的数值，从而使效率下降。

另一方面，如果参与者不按纳什均衡点出招（即不选择2），经济学家关于参与者的行为必有理性的假设就需要修改了。当然，对于人总是基于利己目标作出理性选择这一观点，TD并不是唯一一个提出质疑的博弈模型，但它提出了一个令人更加困惑的问题：即使参与者只关心自己的获利，但对他们来说，按照形式分析的预测出招仍然算不上是理性行为。

TD模型对于我们观察和认识现实世界方面，还有其他一些作用。比如说，它有助于阐明军备竞赛是一个渐进的过程，通过一小步一小步扩充军备的行动，逐渐把人类拖入越来越危险的境地。理论家们也曾尝试进一步发展TD模型，以帮助我们了解彼此竞争的企业为何要竞相杀价以致两败俱伤（不过却让消费者捡了便宜）。

考虑到所有这些因素，我们不得不提出两个问题：真正玩这个博弈对局时，人们究竟会怎样出招？如果大多数人都选择比2大得多的数，那么我们如何解释博弈论无法预见到这一结果的事实？关于前一个问题，我们已经掌握了相当多的资料，而关于后一个问题，迄今仍然知之甚少。

耐人寻味的实验结果

过去10年中，研究人员对TD模型进行过多次实验，从中获得一些相当深刻的启示。C·莫妮卡·卡普拉（C. Monica Capra）、雅各布·K·戈埃雷（Jacob K. Goeree）、罗萨里奥·戈梅（Rosario Gomez）和查尔斯·A·霍尔特（Charles A. Holt）等人，在美国弗吉尼亚大学用真钱进行了一项非常著名的实验。实验规定，参与的学生每人可获6美元报酬，并且他们在对弈过程中赢的钱也统统归自己所有。为了使实验预算不致失控，参与者们选择的数字是以美分而不是美元来标价的，选择范围在80到200之间，而惩罚与奖励的额度则随对弈轮次的不同而变，最低只有5美分，最高则达到80美分。实验人员希望了解，调整惩罚与奖励的数额是否会对参与者们如何出招产生影响。对于形式分析来说，改变奖惩额度不会产生任何影响：无论奖惩多少，反向归纳法得出的结果总是（80，80），这正是这项对弈的纳什均衡点。

实验证实了我们的直观预想：参与者总的说来不会按纳什均衡的策略出招，即不会选择80。当奖励额为5美分时，参与者选择的数字平均为180，而当奖励额涨到80美分后，这一平均值下降为120。

卡普拉及其同事们还让参与者反复进行TD对弈，考察他们的行为是否会有什么变化。即使选择纳什均衡点不会是他们的第一直觉，但在反复对弈的过程中，他们能学会按纳什均衡的策略出招吗？果然，当奖励数额较大时，参与者们的选择出现了逐渐降低并向纳什均衡点（即80）靠拢的趋势。然而值得注意的是，当奖励数额较低时，参与者们的出招却出现了向另一个极端（即200）攀升的趋势。

在对弈中，参与者通常都不会选择纳什均衡点。2002年到2004年间，以色列特拉维夫大学和美国纽约大学的阿里埃尔·鲁宾斯坦（Ariel Rubinstein）进行的一项网上实验，进一步证实了这一事实。这是一项虚拟实验，不会真的付钱给参与者。参与对弈的都是打算去听鲁宾斯坦介绍博弈论与纳什讲座的听众，他们要在180到300之间选择一个整数，并把它当成是美元。奖励/惩罚数额定为5美元。

来自7个国家的大约2,500人参加了这项实验，样本量之大、参与者范围之广，都是实验室中的实验所望尘莫及的。所有参与者中，选择纳什均衡点（即180）的人不到1/7。55%的人选择了最大的数，即300（参见第74页图示）。出人意料的是，如果我们把参与者划分为若干组（例如把来自不同国家的人划入不同的组），各组间得出的实验结果是非常相似的。

究竟是怎样的思维过程，导致参与者的选择形成了这样一种分布呢？答案迄今仍不得而知。特别有趣的是，参与者最热衷的选择（即300）恰恰是这个博弈模型中唯一一个“被支配”的选项——也就是说，总是存在另一个始终不会比它差，有时候甚至比它还好的选择（即299）。

鲁宾斯坦把所有可能的选择分为四组，并推测每一组背后均与一个不同的认知过程相关。300是参与者本能得出的选择。而在295到299之间选择一个数，则需要运用智谋进行一番推理（比如一定程度的反向归纳）。选择181到294之间的数完全是随机决定的。最后，参与者如果选择180，则可以用标准博弈论来解释。不过他们也许并不知道什么博弈论，而是自己想到了这一招，或者是事先就对这个赛局有所了解。

如果我们想检验鲁宾斯坦对上述3个组的推测是否正确，可以统计一下每位参与者做出决策所花的时间。事实上，选择295到299之间的数的参与者，平均所花的决策时间是最长的（96秒），而选择181到294之间的数以及选择了300这个数的参与者，平均所用时间为70秒。这个结果与鲁宾斯坦的推测不谋而合，即在295到299之间作出选择的参与者比作出其他选择的参与者盘算得更多。

在TD实验中，为何如此之多的参与者对纳什均衡点敬而远之？博弈论学者尝试解开这一奥秘。某些分析家认为，许多人不会进行必要的演绎推理，作出了并非他们本意的非理性选择。这种解释在某些情况下肯定是错不了的，但它不能解释所有的实验结果。2002年，在德国霍亨海姆大学的蒂尔曼·贝克尔（Tilman Becker）、米夏埃尔·卡特（Michael Carter）和约尔格·内韦（Jorg Naeve）得到的实验结果，就不能用它来解释。在这项实验中，51位博弈论学会会员参与了选择范围为2到100的原始版TD模型的对弈。每位参与者都要事先选定一个策略，并发送给主持实验的研究人员。研究人员按照他的策略出招，让他跟其他50名对手中的每一位“虚拟过招”。参与者既可以选中一个数，在每局对弈中都用它出招，也可以选择一组数，并附上每个数在50局对弈的出招频率。这场博弈实验还有真钱奖励机制：实验人员将随机挑选一位参与者发放奖励，奖额为20美元乘以该参与者在50局对弈中的平均收益值。结果，那位幸运获胜者的平均收益为85美元，最终得到了l,700美元的奖励。

51位参与者中，有45人只选了一个数（其余6人则选择了多个数字）。在这45人中，只有3人选择了纳什均衡点（2），10人选择被支配选项（100），23人选择95到99之间的数。按理说，博弈论学者应该懂得如何进行演绎推理，但即使是他们，也没有作出理论上所要求的“理性”选择。

表面上看来，他们这样选择的原因似乎不难理解：大多数参与者都准确地判断出，他们的对手大都会在95到99之间作出选择，因此挑选一个差不多大的数便可获得尽可能高的平均收益。为何每个人都预料其他人会选择一个较高的数呢?

或许除了利己动机之外，利他主义同样也深深扎根于我们的灵魂深处，我们采取何种行为则是这两种思想较量的结果。我们知道，如果我们都选择l00，那么航空公司经理付给我们的钱是最多的。许多人都不好意思为了多赢区区一美元而挖同行旅客的墙脚，因此，尽管我们完全明白，从理性的角度分析，99对于我们个人来说是更好的选择，但我们还是宁愿选择100。

为了进一步解释我们在这类实验中观察到的其他行为，部分经济学家提出了一些更严格的、相当牵强的假设，用基于这些假设的复杂模型来解释观测到的行为。为了迎合数据，这类模型和假设会变得愈来愈复杂。但它们越是复杂，我们从中能获得的见识就越少。

不平坦的未来之路

不过我们依然面临挑战，这一挑战并不是如何解释普通人在参与TD对弈时的真实行为。实际上，上述实验似乎表明，利己思想、社会化以及不完善的逻辑推理都有可能支配着大多数人的抉择。然而，我认为，即使把这三个因素全部排除在外，也不会有很多人选择2。如果大多数人并不缺乏演绎推理的能力，并且尽量克制住自己正常的利他思想和社会行为，铁了心只顾赢到尽可能多的钱，却依然选择较大的数（或许是90以上的数），这种情况又该如何解释呢? 现代博弈论研究的大多数问题可能涉及相当多的数学内容，不过一旦掌握其方法，问题就迎刃而解了。但这个问题却不同，解决它的难度相当大，可能需要创造性的新思维。

假定你和我都属于这类精明而冷血的参与者，那么我们在对弈时会如何思考呢？我预料你会选一个较大的数，比如说90到99之间的某个数。那么我就不应该选99，因为无论你选择此区间中的哪一个数，对我来说选择98的结果都不会比99差，甚至可能更好一些。但如果你跟我一样，知道对手是无情的冷血动物，并且按照同样的逻辑进行思考，那么你也不会把99作为自己的选项。这样，顺着当初导致露西和皮特双双选2的推理轨道，我们转眼间就把90到99的所有数都排除在外了。所以，我们不可能指望“冷酷无情之人会合理选择的一组大数”是一个意义明确的集合。而当我们试图把逻辑推理运用于本质上难以明确界定的前提时，我们实质上已经进入十分棘手的哲学领域了。

如果是我来玩这个赛局，我将告诫自己：“赶快把那些博弈论的逻辑忘到九霄云外。我要选一个大数（可能是95），而且我知道我的对手出招也跟我差不多。我还知道，对于那些理性论证，诸如下一个较小的数会比我们已选择的数更好云云，我统统都会置之不理。”有趣的是，这种态度表面看来拒绝了形式理性和逻辑，实际上却含有一层后理性主义的色彩。如果两位参与者都按这种后理性的路线行事，结果将实现双赢。用理性态度拒绝理性行为，这是一个很难形式化的概念。如果我们真要破除那些体现在游客困境中，且长期困扰着博弈论的理性悖论的话，这将是我们未来不得不攻克的一个难关。