互动科普

撰文/樊隽轩 叶法丞 冯伟民

定量地层学方法

岩层中保存的化石记录是丰富多样的，但其中能直接用于地层划分与对比的标准化石通常只占极少的一部分。因此，传统的生物地层研究会仅仅利用1/10甚至1/100的化石信息进行地层划分和对比，而其他大多数的化石信息都被舍弃了。从数据精度来看，这是一种数据上的浪费。难道这些被舍弃的化石信息真的对地层对比毫无用处吗？ 我们可以从数据的角度来思考这一地层学的科学问题。

建立生物地层序列，可以看做是对所有化石的首现事件和末现事件的排序，这一排序的结果，必须符合基本的地质规律，比如某种化石的首现事件必须在其末现事件之前，生物不可能先灭绝然后才出现；如果在观察到的化石记录中化石A和B在同一个样品中出现了，那么排序的结果中这两种化石也必须有共有部分，诸如此类。于是，我们就可以将一个复杂的地质学问题转换为一个满足一定条件的简单的排序问题。

假设有两种化石，分别是化石A和B，在满足同种化石的首现必须早于其末现的条件下，排列组合的可能共有6种（下图）。假设我们在两个剖面中发现了这两种化石，在剖面I中，化石A的延限（即从化石A的首现至其末现的这一连续时段）涵盖了化石B的延限（下图右上）；在剖面II中，化石A的延限整体晚于化石B的延限（下图右下）。由于在剖面I中我们发现化石A和B在同一层共生，因此序列1和序列6的可能性被排除，还剩下4种可能。

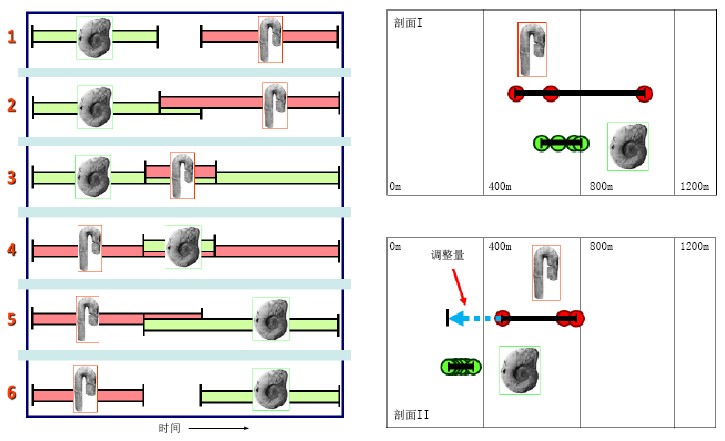
图. 左图为可能的化石排列，右图为剖面I和剖面II中实际发现的化石位置。 图/Peter Sadler

由于化石记录是不完整的，因此，当发现化石记录与我们建立的虚拟的化石排列不吻合时，我们可以对剖面中观察到的化石延限进行外延，从而使化石排列与假定的序列吻合。比如，对于假定的序列4，剖面I中化石A和B的延限与之完全吻合，即A的首现早于B的首现，A的末现晚于B的末现；剖面II中，只需要将化石A的首现下拉到与化石B的首现相当的位置，则化石A和B的延限便能与序列4完全吻合。我们将化石A的首现下延的这部分延限称为化石A的延限调整量。而对于序列2、3和5，需要对两个化石的延限都进行调整，方可满足。我们将为了满足某个假定序列而需对各个剖面的每个化石进行的调整量进行累加，就可以得到该假定序列的调整总量。调整总量最小的序列即最优序列，也就是该地层对比问题的最优解。在上述问题中，序列4所需的调整量最小，因此为该问题的最优解。

对于两种化石，可能的序列是6种；三种化石，可能的序列是90种；四种化石，可能的序列是2520种；七种化石，可能的序列是6.8亿种；如果是100种化石，则可能的序列是10300！而实际的地层对比问题所面对的数据集规模更是远远超过了上面的数字。美国加州大学河滨分校的Sadler等在2009年研究笔石动物的演化历史时，其数据集达到了2090个化石物种；澳大利亚墨尔本大学的Alroy在上世纪90年代研究北美陆生哺乳类的演化时，涉及3243个化石物种的延限数据。因此，对于此类常见的地层学问题，我们不可能采用穷举法将所有可能的序列都排查一遍，找寻调整总量最小的最优序列。

在数学领域有一个著名的难题，即旅行商问题（traveling salesman problem，TSP）。有n个城市，一个推销员要从其中某个城市出发，走遍所有的城市，再回到他出发的城市，求最短的路线。仔细思考一下就可以发现，上述的地层学排序问题与旅行商问题有着许多可类比之处。地层中生物的首现与末现事件，对应于旅行商问题中的城市；生物事件序列，对应于可能的路径；符合所有地层剖面的最优生物事件序列，对应于最短路径。因此，旅行商问题的许多解法，如模拟退火算法、遗传算法，也适用于地层的生物事件排序问题。

基于这样的思路，Sadler教授于1998年起开始着手开发定量地层学软件CONOP。CONOP是Constrained Optimization的简写，即约束最优化法。约束指CONOP的两个主要约束条件，即化石的首现必须在其末现之前，以及在地层剖面中实际观察到的化石共生现象，在最终序列中也必须存在；最优化指最终获得的序列应该是可以用某种方法度量（比如延限调整量最小）的最优解或局部最优解。定量地层学方法的出现，尤其是如CONOP这类自动地层对比软件的出现，使得基于地层古生物大数据进行相对年龄的确定成为可能，并使得传统的地层学研究向着定量化、精确化的方向继续前进。

（本文发表于《科学世界》2015年第11期）