互动科普

奇妙的量子霍尔效应

在霍尔效应被发现约100年后，德国科学家克劳斯·冯·克利青（Klaus von Klitzing）发现，二维半导体材料的霍尔电阻，在低温强磁场下与外加磁场不是简单的线性关系，而是会出现一个个的平台。在平台处，霍尔电阻严格等于一个常数（h/e²）除以正整数 [比如h/(2e²)、h/(3e²)、h/(4e²）等，这里e是电子的电荷，h是普朗克常数]，这就是整数量子霍尔效应。由于这一重大发现，冯·克利青获得了1985年的诺贝尔物理学奖。1982年，美籍华人物理学家崔琦（Daniel Chee Tsui）和德国物理学家霍斯特·施特默（Horst Stormer）在更强磁场下研究更高质量的二维砷化镓异质结时，发现霍尔电阻可以在量子电阻h/e² 除以1/3和2/3等分数处形成平台，即分数量子霍尔效应，这个效应不久由另一位美国物理学家罗伯特·劳弗林（Robert Laughlin）给出理论解释，他们三人因此荣获1998年的诺贝尔物理学奖。

整数量子霍尔效应物理机制可以用朗道能级予以解释。在二维系统中，经典力学告诉我们，处于磁场中的电子，由于洛仑兹力的作用会形成圆周运动的回旋轨道。在量子力学中，这些轨道是量子化的，且具有分立的能级：E_n=(h/2p)w_c (n+1/2），w_c=eB/m是电子的回旋频率。这些量子化的轨道最先由前苏联物理学家列夫·朗道（Lev Landau）提出，因此被称为朗道能级。如果此时电子总共占据了N个朗道能级，此时得到的霍尔电阻的平台正好对应h/e²除以N。对于分数量子霍尔效应，其形成原因需要用复合粒子予以解释，比较复杂。

整数量子霍尔效应每一个量子平台对应的量子电阻都严格等于h/e²除以正整数，并且极稳定，精确度可以达到10^-8量级甚至更高。因此，国际计量委员会从1990年1月1日起，在世界范围内启用量子霍尔电阻标准代替原来的实物电阻标准，并给出量子霍尔电阻的标准值R_K=h/e²=25812.807Ω，对应于N=1平台处的量子霍尔电阻值。

量子霍尔效应之所以如此重要，一方面是由于它们体现了二维电子系统在低温强磁场的极端条件下的奇妙量子行为，另一方面这些效应可能在未来电子器件中发挥特殊的作用。当二维半导体处于量子霍尔态时，导电是通过电子在样品边缘沿着准一维的边缘态（一维通道）运动而进行的。由于外加磁场赋予这些边缘态拓扑的手性特征（电子只能沿着一个方向运动），电子碰到杂质时会绕一个弯继续向前走，不会因为散射而返回来。由于电子散射是电子减速并产生能量耗散的主要来源，因此我们说，在量子霍尔态电子的运动是弹道的、无能量损耗的，可以用于制备低能耗的高速电子器件。例如，如果把量子霍尔效应引入计算机芯片，将会克服电脑的发热和能量损耗问题。

量子自旋霍尔效应

电子除了可以平动外，自身还具有一个非常重要的内在性质，就是自旋。我们知道，陀螺在平面上运动的同时，自身还在不停地旋转，这种旋转可以是向左旋也可以是向右旋。类似地，电子自旋也可以分为上自旋态和下自旋态。处于不同自旋态的电子的行为，往往会很不一样。

与量子霍尔效应一样，量子自旋霍尔效应也是在二维体系中由边缘态引起的量子效应，不同之处在于，量子自旋霍尔效应是由两组自旋方向相反、运行方向也相反的边缘态组成，并且不需要外加磁场。因为两组边缘态上的电子是沿着相反方向运动的，所以净电荷电流为零，不存在霍尔电导。但是由于它们具有相反的自旋方向，从而形成了量子化的自旋霍尔电导（2e/4p），因此被称为量子自旋霍尔效应。

首先在量子自旋霍尔效应上取得重大突破的是美国斯坦福大学的张首晟教授研究组。通过理论分析，他们在2006年预言了在HgTe/CdTe半导体量子阱结构中，通过调节HgTe的厚度有可能实现量子自旋霍尔效应。2007年，德国伍尔兹堡大学的研究组成功地在HgTe/CdTe量子阱结构中首次观测到这种特殊边缘态的量子效应，从而在实验上证实了斯坦福研究组的预言。这一工作在当时引起了很大的反响，2007年末，美国著名的《科学》（Science）杂志评选出了当年的十大科技进展，斯坦福大学与伍尔兹堡大学研究组的工作成功入选。这一轰动性的事件，标志着对于拓扑绝缘体的研究从前期的理论研究为主过渡到以实验探索的新阶段。量子自旋霍尔效应的边缘态，依然是无能量耗散的，可望应用于下一代自旋电子学器件中。

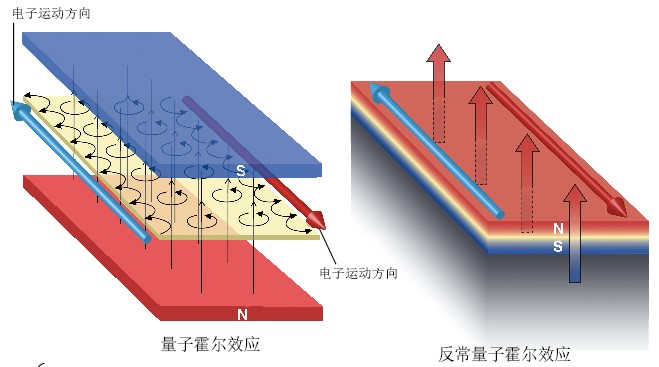
左图：量子霍尔效应原理示意图。当二维半导体材料（淡黄色）处于磁场中时，在洛仑兹力的作用下电子会向边缘发生偏转，但当磁场足够强时，电子在未到达边缘时就完成了一个完整的圆周运动。此时，电子就只能在原地打转而永远都无法走到边界去，就相当于被磁场给囚禁了。可是在边缘的电子情况就完全不同了，由于太靠近边缘，电子还没有完成一个圆周运动就被边缘反弹回来，然后继续圆周运动、继续反弹，如此反复，电子就可以沿着边缘从材料的一端运动到另一端，这就形成了所谓的“边缘态”，也是形成量子霍尔效应的关键。

右图：反常量子霍尔效应原理示意图。如果二维材料本身就具有磁性的话，那就省去了外加磁场的麻烦。材料本身就是一个磁铁，并且在这个磁铁内部的电子也被囚禁，只有边缘的电子参与导电，从而形成量子反常霍尔效应。

量子反常霍尔效应，量子霍尔效应家族的最后一个成员

霍尔效应在强磁场中可以实现量子化的霍尔效应，那么反常霍尔效应能不能实现量子化的反常霍尔效应呢？如果能够实现，这将是又一个全新的量子效应，有可能是量子霍尔效应家族的最后一个重要成员。量子反常霍尔效应是一种不需要外磁场的量子霍尔效应，只具有一个边缘态且电子自旋都朝相同方向，因此霍尔电阻恰好为h/e²（约25.8kΩ）。

由于量子霍尔效应的产生需要用到非常强的磁场（约为地磁场几十万倍），要产生强磁场不但价格昂贵，而且其体积庞大（衣柜大小），很难在人们日常生活中得到广泛应用。所以如果能实现反常量子霍尔效应，我们就可以摆脱强磁场的限制，利用其无耗散的边缘态发展新一代的低能耗晶体管和电子学器件，从而解决电脑发热问题和摩尔定律的瓶颈问题，进而有可能推动信息技术的革命。因此，从理论研究和实验上实现量子反常霍尔效应，成为世界凝聚态物理学家关注的焦点。

也许将来的某一天，量子反常霍尔效应能够得到广泛应用，现在的超级计算机也许就可以做成笔记本电脑那么大，并且不需要风扇散热，非常安静。

（本文发表于《科学世界》2013年第6期）