互动科普

其他开局式的解我们就不一一给出了，请读者自己去找。如果你能够在34步到120步之间完成，成绩就很不错了。

非常有意思的是，华容道并非中国的“专利”，世界上许多国家都有类似于华容道的游戏，不过名称不同、故事背景不同而已。下面，我们举几个例子。

20世纪初，在法国出现了一个游戏叫“红鬃烈马”（法文是I’ane rouge，英文是red donkey，直译应该为“红毛驴”）。游戏的目标是使大方块所代表的红鬃烈马冲出重围，从底部开口处逃逸。大家看，这不是同我们的华容道一模一样吗？

1975年，英国剑桥大学的数学家康韦（John H. Conway）推出一个名为“一百步和一百五十步”的游戏（Century and a Half）。之所以取这样一个名称，是因为这个游戏有两个玩法，正好需要100步和150步。游戏的第一个玩法同华容道一样，要求把大方块A移到下方中央；第二个玩法则不但要求把大方块A移到下方中央，而且要求其他棋子所处的位置，恰使整个棋盘如果转180°的话，其布局和开局式完全一样（但棋子编号可以不同）。

这个游戏用100步完成第一个玩法有几种不同的路径；康韦的100步解法的巧妙之处在于：接下去再走50步正好完成第二个玩法。下面我们给出康韦的解法：

56897 42A13 61A24 79815 79816 51984 74865 19684 91586 153A7 91648 53A72 9461A 35861 A2735 86194 A5392 75861 A7249 5381A（100步) 47813 59728 1284A 23623 65897 9863A 47986 52A17 41A25 68973

都来自“重排九宫”？

中国的华容道游戏和外国的类华容道游戏之间是什么关系？学者有不同的看法。有人认为是中国的华容道传入外国，被外国人模仿、利用；也有人认为是中国人借鉴外国的玩具改造成为华容道。不管怎样，中、外的所有滑块类游戏都起源于由我们中国古老的《九宫图》演变而来的“重排九宫”，这一点却是公认的。

所谓九宫图也就是3阶幻方，在3×3的方阵中填入自然数1～9，使每行、每列和2条对角线上3个数字之和都相等。这道“算术题”虽然简单，但是2000多年前我们的祖先发现这一现象，并把它记载在公元80年成书的《大戴礼记》中，绝对是一件了不起的大事，是中国人在数学上的一个伟大创造，并奠定了数学中一个重要分支—组合学的基础。

当然，当时还没有阿拉伯数字，奇数用若干空心圆圈表示，偶数用若干实心圆圈表示，这和中国古时的阴阳学说有关。

在九宫图的基础上，我们的祖先在很早以前就发明了重排九宫游戏。原始的重排九宫游戏是这样的：在3×3的方阵中任意填入1～8这几个数字，留下一个空格。与空格相邻的数字，允许上、下、左、右移动到空格中去。要求最后数字从1到8按顺时针方向排好，或按行或按列顺序排好，空格居中或位于右下角。

重排九宫问题可通过计算机程序用状态空间法来解。如果用0表示空格，那么按从左到右、从上到下的次序，可把初始状态表为〔7，5，6，8，3，2，4，0，1〕，把目标状态（最终状态）表为〔1，2，3，4，5，6，7，8，0〕。可以通过以下23步实现转换：

12653 12653 12487 12487 456

重排九宫是否有解，看布局情况就可以预先判断。其判断准则是：如果由初局到终局相当于偶数次交换2个数字，则有解；如果由初局到终局相当于奇数次交换2个数字，则无解。

在重排九宫问题有解的情况下，一般总可以以或多或少的步数完成任务。但如果要求以最少步数完成从初局到终局的转换，那么难度就大得多了，甚至判断是否是最少步数本身也是一个难题。历史上就有这样一个故事：19世纪的著名娱乐数学专家亨利·杜德尼（Henry Dudeney）在研究如图3的重排九宫问题时，获得了一种需要36步的解法）：

12543 12376 12376 12375 48123 65765 84785 6

在很长时间里，这36步解法被认为是该问题的最佳解法，没有人提出怀疑。直到后来通过计算机一下找到了解决该问题的10种30步解法，才打破了对杜德尼的迷信。

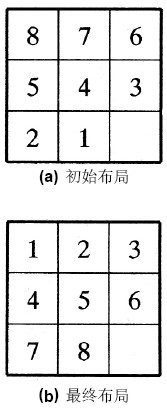
杜德尼的重排九宫

（本文发表于《科学世界》2013年第12期）