互动科普

现在已经有可能控制某些混沌系统。工程师们能利用混沌来稳定激光器、电子电路，甚至动物的心脏。

混沌有何用?有些人会说它是不可靠的，不可控制的，因此是无法利用的。确实，没有人能精确预测在一个较长的时间里，混沌系统会如何表现。为此，工程师们通常总是用同一方法来处理混沌：避开它。我们认为这种策略有点目光短浅。在过去几年中，我们与同事们一起验证，混沌是可以控制的，可以利用的，甚至是十分可贵的。

混沌已被用来增强激光器的功率；调整电子电路的输出，使之同步；控制化学反应的波动；稳定动物有病的心脏的错误心律；编码电子信息以保证通讯安全。我们预期，在不久的将来工程师将不再回避混沌，而是利用混沌。

至少有两个理由可以说明混沌是有用的。首先，一个混沌系统的行为是许多有序行为的集合，但每一个有序行为在正常条件下都不占主导地位。近年来，研究人员已经证明，如果以适当的方式来扰乱一个混沌系统，就能促使该系统以它许多有序行为中的一个来起作用。由于混沌系统能迅速地在许多不同的行为方式之间进行转换，它们就特别灵活。

其次，虽然混沌不可预测，它却是确定的。如果两个几乎相同的具有适当形态的混沌系统受到一种相同信号的驱动，即使没有人能说出其结果，它们也会产生相同的输出[见本期业余科学家”]。这种现象已经在通讯业造就了许多种令人感趣的技术。

一个多世纪以来，混沌几乎只是少数几个理论工作者研究的对象，人们相信他们必定能开发出能作为所有混沌应用方法之基础的概念。大多数自然系统都是非线性的：行为上的一个变化并不是条件上的一个变化的简单函数。混沌就是非线性行为的一种形式。混沌系统的显著特征是，它们对初始条件表现出一种灵敏性。更强调一点来说，如果两个几乎相同的混沌系统处于两种略为不同的状态时，它们将迅速演变到两种极为不同的状态。

乍一看，混沌系统似乎以一种随机的方式起作用的。然而，深入的研究表明，它们具有一种潜在的次序。为了观看任何一种系统的动力学状态,150多年前爱尔兰出生的物理学家William Hamilton和德国数学家Karl Jacobi以及他们同时代的科家提出了解释非线性动力学状态所必须的一个基本概念:状态空间。

能用一个数学公式描述的任何混沌系统具有两种变量:动态变量和静态变量。动态变量是始终在发生变化的基本量。对于一个混沌机械来说，动态变量有可能是一个运动部件的位置和它的速度。静态变量也可以称为参数，它们被设定在某一点上，以后就永不改变了。对于一个混沌机械来说，静态变量有可能是某一部件的长度或一台电机的速率。

状态空间基本上是一幅坐标图，其中每一根轴都与一个动态变量相对应。状态空间中的一个点代表系统在一个特定时刻中的状态。当这个系统发生变化时，它就从状态空间中的各点之间发生移动，定义出一条轨迹，即曲线。这条轨迹代表了这个动态系统时间变化的情况。

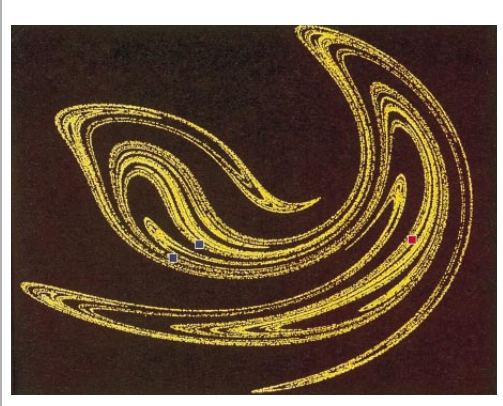
在状态空间中，混沌系统具有十分复杂的轨迹。相反，线性系统具有简单的轨迹，例如42页框图中的一些圈。然而，一个混沌系统的轨迹并非随心所欲的，它通过状态空间的某些区域却避开另一些区域。这种轨迹被拉向一个所谓的混沌吸引区，在某种意义上来说，吸引区是一个混沌系统的本质所在。混沌吸引区是那些固定的参数以及那些决定动态变量数值的方程的表征。沌吸引区，在某种意义上来说，吸引区

因此，测量一个混沌系统的轨迹并不能预测在遥远的将来某一时刻该系统将处于吸引区的哪一点上。另一方面，无论在什么时候去测量它，混沌吸引区总是保持不变，研究人员一旦获得了关于一个系统的混沌吸引区的信息，他们就能着手利用混沌。

1989年，作者之一的Pecora发现，一个混沌系统可以构筑成其各部件完全同步地起作用。众所周知，孤立的混沌系统是不能实现同步的。如果能建立两个分隔但实际上却相同的混沌系统，由干两系统间的任何微小差异都会被放大，它们很快就步调不一致了，然而在某些场合，一个系统的部件可以装配成呈现相同的混沌行为，事实上，这些部件相互间可以处于很远的距离，这样便可以利用同步化的混沌来进行通讯。

为了建立一个部件同步的混沌系统。,就有必要了解稳定性这个概念。当一个系统受到一些干扰时，如果它在状态空间中的轨迹只比它在无干扰条件下所应有的轨迹发生很的变化，这个系统就是稳定的。俄国数学家Aleksandr M．Lyapunov认识到，可以用一个数来代表由一个扰动引起的变化。他用前一时刻该扰动的大小来除这一时刻该扰动的大小。然后他以不同的时间间隔作同样的计算，再把结果取平均值。

这一称为Lyapunev(李雅普诺夫)乘数的量，描述了一个扰动在平均情况下将作多大的变化。如果Lyapunov乘数小于1，扰动趋于消失，系统便稳定。如果该乘数大于1，干扰就增大，系统就不稳定。所有的混沌系统都有一个大于1的Lyapunov乘数，因此总是不稳定的。这是混沌不可预测性的根源。

一个混沌系统的部件假如要实现同步的话就必须是稳定的。这并不意味着整个系统不能是混沌的。如果两个相似的稳定部件用相同的混沌信号躯动，它们都会呈现混沌行为，但它们将抑制而不是扩大它们之间的任何差异，从而为同步混沌创造机会。

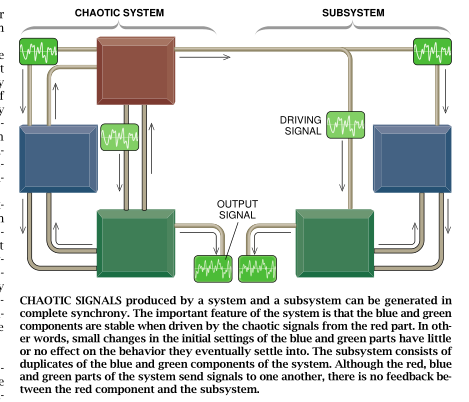
由pecorn和美国海军研究实验室的Themas L．Corroll开发的一种设计方案采用了类似同步化机构的一个普通混沌系统的子系统。他们首先把这个同步化的子系统从其他支撑部件区分开来，然后复制了同步化子系统(见图3和图4)。随后，支撑子系统给原来的同步化子系统和它的复制品提供一个驱动信号。

如果同步化子系统具有小于1的Lyapunov乘数，也就是说，如果这些子系统是稳定的，它们将表现出混沌行为，但又将是完全同步的。子系统的稳定性保证任何小的扰动将会被抑制掉。因此不论信号多么复杂，同步化子系统将实际上以同样的方式对来自支撑子系统的信号作出反应。

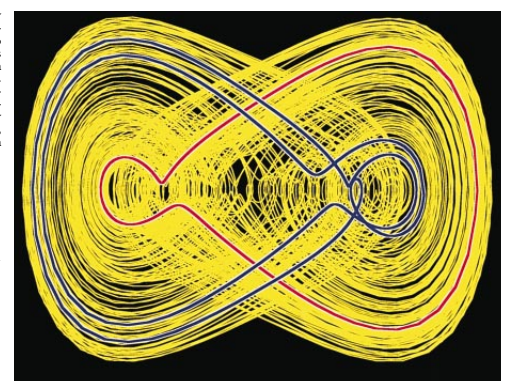
为了率先演示同步化的混沌，Pecora按照Lorenz混沌系统发明了一种计算机模拟法。1963年美国气象学家Edward N．Lorenz在利用计算机研究天气时发现了混沌行为，Lorenz混沌系统就是以他的名字命名的。Lorenz系统有三个动态变量，因此这种系统的状态空间图是三维的。在状态空间中描绘Lorenz系统的轨迹后揭示了所谓的Lorenz混沌吸引区[参见1987年4月号“科学”JamesP．Crutchfield．J．DoynaFarmer，NormanH-Packard和RobertS．Shaw所著“混沌现象”]

为了进行计算机模拟，Pecora从Lorenz系统的三个动态变量开始，选择其中的一个作为驱动信号。子系统由剩下的两个动态变量构成，再复制一个子系统。虽然子系统和它的复制品起先被设定为产生不同的输出，它们很快就趋同，发出同步的混沌信号。在状态空间中，这两个子系统从不同的点出发，互相追赶，并步调一致地围绕它们的混沌吸引区相伴运动。

在作出这一发现之前，科学家们没有理由相信一个子系统的稳定性可以与该系统的其余部分的稳定性相对独立。也没有谁认为一个非线性系统在一个混沌信号的驱动下可以是稳定的。

稳定性不仅取决于子系统本身的性质，也取决于驱动信号。在某一种混沌信号的驱动下一个子系统可能是稳定的，但在另一种混沌信号的驱动下却可能是不稳定的。奥妙在于找到那些对混沌信号作出稳定反应的子系统。在某些场合，一个子系统的稳定性可以通过利用一个数学模型来估计，但通常来说，这种预测是很困难的。

有关同步化混沌的实验才刚刚开始研究。1989年，Carroll构筑了第一个同步化的混沌电路，通过复制一个呈现混沌行为的电路的一倍分，他创造了一个其子系统和子系统的复制品由同样的混沌信号所驱动的一个电路。这两个子系统所产生的电压确实是以一种混沌的方式波动的，但它们却又总是相互同步的。

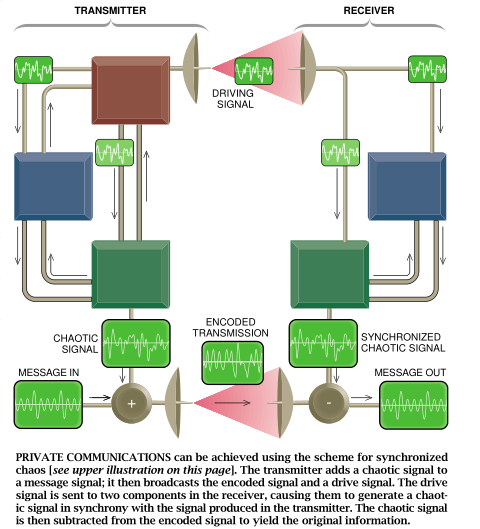
Carroll认识到，他的同步化混沌电路有可能用于保密通讯。例如设想有一位比尔先生想发一份秘密电报给艾尔先生。比尔有一个产生混沌躯动信号的装置，他还有一个能以稳定方式响应该信号的子系统。艾尔有一个该子系统的复制品。比尔把他的秘密电报翻译成电子信号并把电子信号与他的子系统的混沌输出相组合。然后比尔把编码了的电报与驱动信号一起发送出去。

任何一个截获这些信号的人能探听到一些混乱的噪音，从中提取不到任何信息。(当然，除非他或她能设法弄到一份比尔或艾尔的子系统的复制品。)当艾尔收到了驱动信号后，他把它输过他的子系统，该子系统再次产生比尔的子系统的混沌输出，随后，艾尔就能从编码的信息信号中删去这一混沌输出，恢复秘密电报。

正如Carroll所演示的那样，恢复隐藏在混沌之中的信号是极其容易的。然而，要建立一个可供实用的秘密通讯系统。工程师们可能需要研制开发些十精密复杂的方案，其中的编码过程不仅仅只涉及到在电报信号中添加混沌信号。

麻省理工学院、华盛顿州立大学和伯克利加州大学的研究人员现在正在建造新的混沌子系统组合，以进行信号处理和通讯。我们也在继续我们的研究工作，并已发现了一种混沌系统，它能象一个锁相环路那样工作。锁相环路这种装置能与其他装置一起使得调频收音机跟踪发射信号的变化。

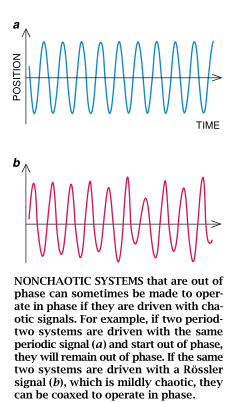
Carroll和Pecora一帆风顺地用混沌信号驱动了混沌系统的稳定部件，这不禁使他们猜测也许用混沌信号来驱动稳定的周期性系统也是理所应当的。他们的直觉引导他们又发现了其他一系列很有前途的应用。设想有两个由相同的周期性信号驱动的系统，它们具有相同的非混沌性周期-2吸引区。“周期-2”这一术语表示，在驱动信号的两个周期中，该系统绕吸引区运动一周。如果两个这样的系统都由同样的信号驱动，但初始时处于吸引区的两端，它们将围绕吸引区旋转，相互间永远不会追上。换言之，如果两个系统出发时异相，它们将永远保持异相。

研究人员最近通过把周期性驱动信号改变为某种类形的混沌信号后发现，两个系统可以耐心处理成同相地进行运作。但并非所有类型的混沌信号都能担任这一任务。某些混沌信号会引起系统本身呈现混沌行为，因此得任何把系统调成同相的机会破灭。为此，工程师们必须为每一种系统寻出类型适用的混沌信号。

优先选择的是最初由Otto E．Rossler发明的一种系统所产生的信号。Rossler信号几乎是周期性的，类似于一种正弦波，其波长与振幅在一个周期到下个周期之间作了一些随机处理。这种称为伪周期性的信号通常只要在周期性信号中加上混沌信号便很容易做到。如果吸引区都是周期一2或更大的几个相同的系统用适当的伪周期性信号驱动的话，它们都会趋于同步。

这种应用是由Carroll于1990年首次推出的。他装了一套电子电路，它有几个周期一2吸引区，由Rcssler型信号及其他几种伪周期性信号中的一种来驱动这些电路。在每个场合，他都发现他能解决异相的问题。然而这些电路在短时间内却又变成异相的了。之所以如此是因为不可能装配出几个完全同样的电路。但要让这些电路在90％的时间内保持同步是很容易实现的。

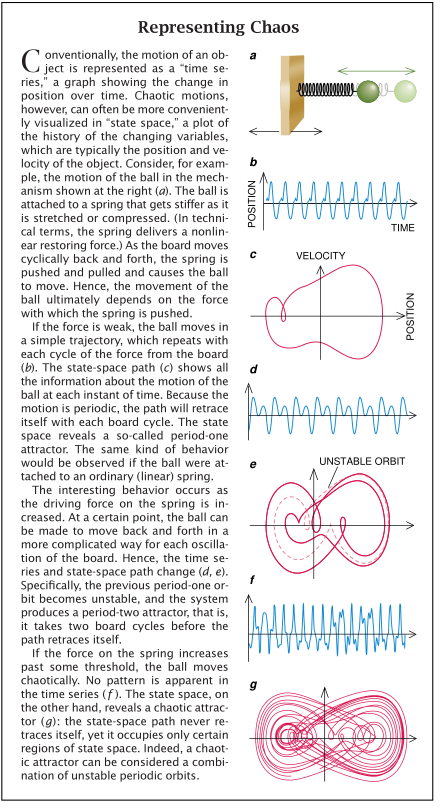
正当一些研究人员忙于寻找混沌的用途时，其他一些研究人员却在设法控制混沌。这一努力的关键之一在于认识到一个混沌吸引区是一些不稳定的周期性行为的无穷集合。表达这一点的最简便方法是设想一个由一个重锤、一根“非线性”弹簧和一台电动机组成的系统，弹簧的一端悬挂在电动机上，另一端连接在重锤上。电动机用一个可调节的力把弹簧提升下降。该系统的动态变量是重锤的位置和它的速度，这些变量决定状态空间。如果电动机的驱动力很弱，重锤将随着电动机每转动一周而上下运动一次。与此同时，重锤上升得快，下降得慢，因此状态空间中的轨迹是单独一个圈，在技术上称之为周期一1轨道。

如果电动机的驱动力增大一些，周期一1轨道变成了一种不稳定行为，重锤将随着电动机每转动两周而上下运动一次。在状态空间中的轨迹现在成了一个双圈，即周期一2轨道如果驱动力再次增大，周期一2轨道也变得稳定了，会出现一种周期—4轨道。事实上：如果驱动力足够的大，所有的周期性轨道都会变得不稳定，将会出现一个混沌吸引区。严格地说，混沌吸引区是一些不稳定周期性轨道的集合。

四年前，马里兰大学的Edward Ott，CelsoGrebogi和JamesA．Yorke提出了一个方案，其中的一个混沌系统能受激遵循状态空间中的一个特殊的不稳定轨道。因此，该方案能够充分利用构成该混沌系统的大量可能存在的行为。

由Ott、Grebogi和Yorke所设计的方法(称为OGY法)在概念上是一目了然的。一开始通过分析一片混沌吸引区可以获得该混沌系统的信息。在收集了这一称为庞加莱(Poincare)截片的信息后，就让这一系统开始运转，等到它几乎在该截片中出现所预期的周期性轨道。然后，通过干扰某一适当的参数让该系统保持在这个轨道上。这一方法的长处之是，它不需要混沌系统的一个详细模型，而只需要庞加莱截片的某些信息。正因为如此，在控制各种各样混沌系统时这一方法一直行之有效。

0GY法的具体困难是，如何获得庞加莱截片，及随后计算出控制干扰。获得庞加莱截片的最简单方法之一是按一定的间隔来测量该系统在状态空间中的轨迹位置。例如，可以在驱动信号的每一周末尾进行测量。这一技术可以画出一张图，其中一个周期一1轨道表现为一个点，一个周期一2轨道表现为两个点，以此类推。

为了计算出控制干扰，可以分析庞加莱截片以决定该系统如何达到所需的轨道，即固定点。这种分析需要三个步骤。首先要确定系统朝固定点会聚或从固定点发散的方向。然后要取得会聚率或发散率，这种比率与Lyapunov乘数相关。最后必须算出，如果控制参数是以一种方式或另一种方式被改变的话，轨道在状态空间中有多大的迁移。这种三步算法提供了决定干扰把系统推向所求周期性轨道的必要信息。

当控制参数实际上被改变时，混沌吸引区便发生迁移，并有些变形。如果一切都按计划进行，新的吸引区便会促使系统继续在所需的轨道上发展。如果系统开始偏离轨道，控制参数就再次改变，产生另一个具有所需特征的吸引区。

这一过程很象在马鞍上平衡一个玻璃球。如果这颗玻璃球一开始是置于马鞍中央的，它趋于向两侧滚动，而不大可能前后滚动。为了不让玻璃球滚动，就需要迅速摆动马鞍。同样，为了补偿系统朝这个方向或那个方向偏离所需轨道的倾向，就需要改换吸引区。就象玻璃球会对马鞍的微小移动作出反应一样，轨道对吸引区的改变非常敏感。Ott，Grebogi和Yorke的研究的与众不同之处是，它证明了混沌的存在可以成为控制动态行为的一个优势。由于混沌系统对初始条件是极其敏感的，它们对所施加的控制也会作出极其迅速的反应。

1990年，我们中的Ditto与海军水面作战中心的MarkL．Spano和StevenN．Rauseo一起，开始试验Ott、Grebogi和Yorke的设想。我们并不期待一帆风顺。没有哪些理论在最初的实验中能站得住脚。但Ott、Grebogi和Yorke的研究却是一个例外。在两个月中，我们在一个相当简单的实验系统中成功地控制了混沌。

这个实验需要一根其硬度可被所施加的磁场改变的金属条。金属条的下端夹在一个底座上。上端可向左或向右晃动。当强度以每秒一周的频率作周期性变化的一个磁场施加到金属条上时，金属条以混沌的方式发生弯曲。第二个磁场起到控制参数的作用。

我们的目标是利用OGY方法来把金属条的混沌运动改变为周期性运动。我们首先需要获得该系统混沌吸引区的一幅庞加莱图。这幅图可以通过每一个驱动周记录一次金属条位置来制作。驱动周就是调制出来的磁场变化频率。用一台计算机储存和分析庞加莱图。然后，计算机能算出该如何改变控制参数，以便使系统能在状态空间中遵循一条周期一1轨道。我们发现，即使存在着噪声和测量误差，也能很容易地把金属条控制到混沌区的一条不稳定周期一1轨道上来。对于实施和控制混沌竟如此容易，我们实在感到吃惊。

有三天时间，金属条一直受到控制，毫无问题。随后，我们感到有些乏味，想试试别的花样。我们尝试着增加外部噪声，改变参数，向来访者展示这一系统(这是让任何实验失败的一条有把握的道路)，以此来让系统失控。此外，我们成功地迫使系统遵循周期一1、周期一2和周期一4轨道。我们能随心所欲地转换这些行为。

就象经常在科学上所发生的那样，新发现会通往意想不到的方向。俄亥俄大学的EarleR．Hunt注意到了我们的实验，决定尝试一下在电子电路里控制混沌。Hunt的电路是用现成的元件装配的。他精心地把这个电路调到具有高达23个周期的轨道，其驱动频率高达每秒5万周。他不仅证明在电子电路里混沌可以得到控制，而且还显示科学的进步可以用很小的代价来实现。

Hunt的混沌控制器采用了OGY法的一个变型，它的优点是不必获得庞加莱截片，控制器所需的信息可以直接从测量混沌行为得到。Hunt电路可以在快速变化的系统中操纵混沌。有了这些成果，Hunt在1991年10月出席了第一届实验混沌大会，当时他已经解决了一个他自己还不知其存在的问题。

在不知不觉中，Hunt克服了让佐治亚理工学院的Rajarshi Roy和他的同事们为难的一个技术障碍。Roy一直在研究激光中的“倍增晶体”效应。这种晶体把入射光的频率加倍，也就是说，把波长减半。Roy所用的激光器发出波长为1064毫微米的红外光。这种晶体则把红外光转换成波长为532毫微米的绿光。然而，晶体的工作并非完美无缺。如果把倍增晶体调到某些方向，绿光的强度会发生混沌性波动。

Roy迫切希望能控制激光装置中的混沌，但他知道OGY法不起作用，因为要获得激光装置的庞加莱截片是十分困难和不切实际的。此外，Roy怀疑一台计算机能否快得足以用于OGY法的计算。幸运的是，在第一届实验混沌大会上他了解到Hunt的研究成果。会后在不到两周的时间内，Roy为他们的激光器装配了一个原型控制器。令他们吃惊的是，第一次试用便成功了。连续几天，他们把激光装置控制到具有高达23个周期，驱动频率达到每秒15万周。

Roy演示，他能控制激光强度的混沌起伏，能稳定高周期的不稳定振荡。激光的能量由此可以降到所需要的频率，而不必在一个很宽的频带上进行分配。(Roy还用这一技术几乎完全消除了他的激光装置上的光强度波动)于是，研究人员能设计出比以前更加灵活更加稳定的激光装置。

激光研究还从混沌控制的另一些进展中获益。例如，海军研究实验室的IraB．schwartz、IoanaA．Triandat、Carroll和Pecora研究小组开发出一种跟踪法，它可以拓展维持混沌控制的范围。对于系统随时间进展而产生的参数变化或因各种原因引起缓慢的参数迁移，跟踪法都能给以补偿。

近几个月来，跟踪法用于混沌电路和激光装置上都取得了惊人的成功。例如，如果控制机构的参数不适合，激光装置只在极有限的功率范围内保持稳定。利用跟踪法，研究人员可以在一很宽的功率范围内维持控制，他们还吃惊地发现，激光装置的输出功率可以提高l5倍。

OGY法的一个问题是，当人们等待系统自然地接近在混沌吸引区中所需的轨道时，时间长得令人难以忍受。Troy Shinbrot及其在马里兰大学和海军水面作战中心的同事们已经验证了一种技术，它能使混沌系统很快地从吸引区中一种任意的初始状态转化到所需的轨道。当Shinbrot和他的合作者们把他们的方法用到那个磁场一金属实验中去时，实现不稳定轨道所需的时间可以减少到原有时间的二十五分之一。

在第一届实验混沌大会上所产生的另一项合作导致了在一个生物系统中实现混沌控制的首项技术的诞生。包括洛杉矶加利福尼亚大学医学院Ditto、Spano、AlanGarfinkel和JamesN．Weiss在内的一个小组研究了一只兔子心脏上的一个隔离区域。通过向冠状动脉注射一种叫作乌本苷的药物能在心肌上引起不规则的快速收缩。一旦这种心律不齐症状开始，我们便用电信号刺激心脏，这种电信号是按照我们根据OGY法设计的一个方案产生的。这些看上去随机的信号足以造成有规律的心跳，有时候还能把心跳降低到正常水平。另一方面，随机的或周期性的信号并不能中止心律不齐，而且常常会使之恶化。

研究人员已经开始测试各种形式的OGY法是否能用来控制人类的心律不齐。他们猜想这种技术有可能用于治疗前房或心室纤维颤动。在这两种征状中，上下心室不规则地收缩，不再有效地泵送血液。在不久的将来，人们有可能研制成采用混沌控制技术的心脏整律器和去纤维颤动器。

科学家和工程师刚刚开始衡量设计那些利用而不是避免非线性和混沌现象的装置的好处。线性系统往往只能干好一件事，而非线性装置却有可能执行几项任务。非线性应用项目有希望做出更灵活、更快速的反应和不同寻常的行为。随着我们继续研究自然界和物理系统的非线性本质，我们不仅能学会与混沌共存，不仅是了解它，而且能学会驾驭它。