互动科普

金融工程能减低经营几十亿美元的一项事业或经营一个小家庭的风险。但这一学科所使用的数学模型可能产生一组新的危险。

在厄尔宠诺效应造成的风暴席卷美国的太平洋沿岸之前几个月，金融界正在为异常天气作准备。从去年开始，一位投资者可以买卖这样一份合约，其价值完全依赖于温度的起伏或雨水、冰雹或雪的积聚。例如，如果从10月到4月洛杉矶机场上的降雨量在17到27英寸之间，这些天气衍生产品就可能兑现。它们是一位保险商应付投保人将来索赔或一位农场主防止作物损失的一种手段。或者这些合约可能允许一位采暖用油的供应商通过购买一份采暖温度一日底价合约(一种合约，它能在温度没有像通常预期的那样降到低于65华氏度的时候对公司进行补偿)，以应付一个比预期暖的冬季而造成的现金亏空。Andrew Freeman是全球天气贸易公司的总经理，该公司位于纽约市，专门从事雨、雪和温度的合约业务。他评论说：“我们是厄尔尼诺效应迷，因为它给我们带来许多生意。”

天气衍生产品是称为金融工程的学科日益热门的一个例子。数学家、物理学家和经济学家的这一高速计算和复杂数学模拟的领域能够有助于调节在经营一项全球业务中所遇到的种种变幻莫测的事态。它需要专门的一揽子证券，来为日元下跌或温度下跌提供价格保险。市场的崩溃或下一次季风的不确定性可以被定价，可以被划分成可上市的份额，可以被卖给某人(他愿意承担那种风险，以换取一笔费用或未来的一系列付款)。康奈尔大学金融教授Robert A．Jarrow说：“这种技术将有效地让你完全掌握整个组织的风险。”

金融工具工程的出现是为了回应近几十年来日益互相交联的世界市场上所出现的动荡：这种动荡是浮动的汇率、石油危机、利率冲击和股市崩盘的结果。新产品的创造性出笼继续伴随着越来越复杂形式的证券和衍生产品一一买卖的特权(指在合约期内按照规定价格买卖指定的股票、货物等的权利)、期货和其他从潜在资产、金融指数、利率或汇率所衍生的合约。新的衍生产品将帮助电力公司防止在新近放宽管制的市场上的价格和容量的波动。信贷衍生产品让银行把呆帐的风险转嫁给其他方。有可能帮助一个企业对付计算机2000年难题的措施已经被认真考虑。

这一活性酵素发生在一个腐朽的背景之下。通过宝洁公司、Gibson礼品公司和巴林银行之类的垮台所积累起来的几十亿美元的损失已经给公众造成了这样一种印象，即那些衍生产品是投机冒险的助长者，而不是新的保险种类。担心还集中在使衍生产品贸易成为可能的那些数学模拟技术的是否完善上。

尽管有这些坏名声，金融工程在去年10月还是获得了一份精美礼物。诺贝尔经济学奖(正式称为瑞典银行经济科学奖)被授予Myron S．Scholes和Robert C．Merton，他们是选择权一定价模型(options—pricing moddel)的两位创造者，这一模型有助于推动衍生产品市场中的交易剧增。

选择权是一种权利(但不是责任)，它允许在某一日期或该日期之前以某一价格买人或卖出股票或某种其他资产。另一大类衍生产品称为期货和远期，它要求买家按一指定价格在某一预定时间内购买一笔资产。还有一类衍生产品称为互换交易(swap)，它允许公司交换现金流一一例如，对固定利率的支付实行浮动利率。金融工程使用这些基本元件来创造专用工具，这些工具有可能为一位退休者的投资提供有保障的最低回报，或允许一家电力公司不必建造新厂而是通过一些合约安排而满足将来的电力需求。

创造复杂的金融工具要求为构成其元件的衍生产品提供精确的定价方法。制定一份期货合约的价格是比较简单的。当小麦成本上升时，小麦期货合约的价格也上升了相同的相对数量。于是，其关系是线性的。对于选择权来说在衍生产品和其背后的资产之间就不存在这样简单的关系。由于这个原因，Scholes、Merton和他们已故的同事FischerBlack的研究就具有了某一位经济学家在介绍他们成就时所说的重要性：这一成就是不仅在金融中，而且在经济学的所有领域中最成功的理论。

爱因斯坦和选择权

在本世纪的大部分时间里，为选择权适当定价一事一直困扰着经济学家。从1900年以他划时代的论文“投机的理论”开始，Louis Bachelier就介绍了一种方法来为选择权定价。令人注意的是，他为这一目的而设想的方程中有一个项预示了一个模型，爱因斯坦后来把这个模型用到了他的布朗运动理论(布朗运动是粒子在流体中的随机运动)。然而Bachelier的方程包含了一些在金融上不现实的假设，诸如股票价格存在负值。

包括诺贝尔奖得主Paul Samuelson在内的其他一些学术思想家们试图攻克这一难题。他们艰难地计算着一个风险升水：选择权价格的一个折扣，以补偿投资者对风险的担扰以及股票在市场中的不确定运动。

Black、Scholes和Merton共有的见识是，不需要对风险升水作一个估计，因为它就包含在所报价的股票价格中，这是选择权方程中的一个关键性输入。市场造成了一种风险较大的股票相对一种较稳当的股票来说，以比它期望的未来价格低得多的价格进行交易，这一价格差异就相当于一种对固有风险的折扣。

在Merton的帮助下，Black和Scholes通过构造一种假想的有价证券提出了他们的选择权定价方程。在这个方程中，股票价格的一个变化通过该股票选择权价值的一个补偿变化而消除了。这种方法称为期现对抵交易，即海静(hedging，指通过卖出或买进期货来对抵目前买进或卖出现货所可能导致的物价波动损失的一种实务)。一个简化的实例是：一份抛出选择权将让持有人有权在三个月中卖出一股股票，如果股票价格是100美元或100美元以下。当该股票下跌1美元时，选择权的值可能上升5O美分(因为该选择权可利用的条件更有可能扩大了)，当该股票上涨1美元时，选择权的值可能下降50美分。

为了冲抵股票价格变化造成的风险，投资者可以为其所拥有的每一股股票买两份选择权：于是利润就能抵销亏损。海静创造了一种没有风险的有价证券，这种证券的回报等同于一张钞票。当股票价格随着时间变化时，投资者必须改变有价证券的构成比例(即股票数与选择权数的比率)，以确保所持证券毫无风险。

事实上，Black、Scholes方程是从一个偏微分方程推导出来的。该方程证明，一份选择权的合理价格是能够从一种海静有价证券中获得无风险回报的价格。由Black、Scholes和Merton所制定的海静法则的变种，已经证明对于金融中心银行具有不可估量的价值，同样也对于其他许多利用这些变量以防止证券因市场变化无常(例如，防止股票急剧下跌)而造成损失的机构具有重要意义。

基本的选择权定价方法也能推广以创造其他工具，有些这样的工具拥有"嘀略"(Cliguet)或"呼喊"(Shout)之类的古怪名称。这些丰富多彩的金融工具提供了构造从选择权到一位客户的特定风险形式的清偿办法的灵活性，例如制定利率或汇率的底、顶或平均函数。

有了正确的选择权，投资者就能赌博或海静任何种类的不确定性，从市场的反复无常(上下运动)到灾难性天气的出现机率。一位出口商可以购买一份“回顾”(1ook—back)外汇选择权，以获得六个月的时期内最优越的美元对日元汇率，而不是在合约到期的那一天去面对汇率的一个突然变化。

在七十年代初期，Black和Scholes的最初论文难以找到一家出版商。到了1973年该论文终于被《政治经济学杂志》发表时，它立即对金融市场造成了影响。在几个月之内，他们的方程被编入了计算机程序。华尔街喜欢它，因为一位交易者只须键人包括股票价格、货币利率和选择权到期日期等少数几个变量就很容易解出该方程。唯一不容易得到的变量是表示“市场反复无常”的变量——股票价格对平均值的标准偏离。然而，这个数字能从过去的价格的上涨下跌中去估计。同样，如果已经知道了市场中目前的选择权价格，一位交易者可以把这一数字输入一个工作站，“回找”出一个反复无常变量数字，该数字可用来判断一个选择权相对于市场上目前的股票价格是否定价过高或过低。

投资者购买了选择权基本上也就购买了反复无常——或者是对市场动荡进行投机，或者是对市场动荡进行防范。市场涨跌越大，选择权的价值越大。以买进选择权(call)进行投机的投资者只可能损失购买的成本(称为升水)，如果股票未能达到购买者可以行使购买它的权利的那个价格。相反，如果股票迅速上涨到超过行使购买权利的价格，获利的空间是不可限量的。同样，海静选择权的投资者也预期前面有一些困难时期，因此为防止市场下跌而购买保护措施。

华尔街的物理学家

虽然可以简便得用袖珍计算器来进行运算，在Black、Scholes方程背后的数学原理却是随机微积分，它是Bachelier和爱因斯坦的研究成果的延续。这些方程对于大多数商业管理教程来说都不是通俗易懂的。进入华尔街而大红大紫的科学家(原先的物理学家、数学家、计算机科学家和计量经济学家)现在正在华尔街的金融机构中发挥着重要的作用。

从同步加速器来到交易厅并不总是会产生一个天衣无缝的转变。在叫作CIBC世界市场的一家投资银行中担任总经理的Charles Smithson指出：“无论什么时候你聘用了一位物理学家，你总是希望他或她不会把市场看作好比是不变的物理定律支配的东西。铀238总是衰变成铀234。但一位物理学家必须牢记，市场能上涨，也能下跌。”

最近，一些大学开设了"定量学校"，它们的课程是向工商管理硕士或其他硕士生讲授金融高等应用数学、Ito定理中的微妙之处和随机微积分中的其他基本原理。它们也可能在物理学家、工程师和数学家涉足华尔街之前对他们进行训练。在麻省理工学院的斯隆管理学院中负责金融工辑教育的AndrewW Lo说:“市场压力导致物理学去接受更多的教育，去理解金融问题背后所存在的动机和直觉。”

作为教育内容的一部分，接受训练的金融工程师要学习超出Black、Scholes和Merton的原始研究之外的数学模拟进展。基本的Black-Scholes方程对市场如何运作做了一些不真实的假设。它把一个固定利率作为输人，但利率当然是要变化的，而且这种变化会影响一份选择权的价值——特别是一份公司债券的选择权。该方程还假定，股票价格增长率的变化构成正态的统计分布，即钟形曲线。在钟形曲线中，事件集中在平均值周围。因此，它没有考虑到像1929年或1987年股票市场崩溃这样的异常事件。Bljick、Scholes和Merton(以及定量学派的追随者）在随后的几年中一直在对原始理论的许多方面进行完善。

Goldman Sachs公司定量战略小组负责人Emanuel Derman是由物理学家改行成为定量金融工程师的，在过去13年中他的工作一直是解决Black-Scholes方程中的不完善之处。Derman是南非开普敦人,1973年以一篇关于亚原子粒子之间的弱相互作用的论文而在哥伦比亚大学获得博士学位。他接着做博士后，包括在宾夕法尼亚大学研究中微子散射问题和在牛津大学理论物理系研壳粲夸克的产生。七十年代后期Derman决定走出象牙塔:“物理学是一种寂寞的工作。它真正是一个精英汇萃之地。在物理学中，你有时候感到你或者是费因曼(RichardFeynman)或者什么都不是。我喜欢物理学，但也许我并不曾像我本该成为的那样出色。”

于是在1980年，他投身到新泽西州的贝尔实验室，在那里他研究—种改造后用于金融业务的计算机语言1985年，GoldmanSachs公司聘用他来开发模拟利率的方法。此后除了有一年服务于沙罗门兄弟公司之外,他一直在该公司工作。在GoldmanSachs公司，他遇到了被聘不久的FisherBlack,他们两人与另一位同事WillianW.Toy —起开始研究为债券选择权定价的一种方法。在Derman的印象中，Black是一位直率真诚的人，手上戴着一块卡西欧数字表，写作习惯十分谨慎小心。Derman说:“Black的数学水平不如他的直觉能力。但他总是对于什么是正确的答案有个主意。”

物理对金融

Derman最近关于股票价格的预期起伏性研究是继续完善他1973年的原始论文。Derman指出，Black-Scholes方程对金融工业的重要性正如牛顿力学对物理学的重要性。“Black-Scholes方程是该领域赖以立足的基础。除了拓展它，没有人知道下一步该干什么。”但是他担心，该领域也许永远不会成功地产生自己的爱因斯坦——或某种包容一切的统一金融理论。金融与物理的不同之处在于，没有一个数学模型能够抓住造成重大市场动荡(如最近的亚洲金融危机)的那些不断变化的大量经济因素。Derman宣称:“在物理学中，你是与上帝比赛。在金融业中，你是与人在比赛。”

在华尔街之外，物理概念与金融之间的类比有时候被学术界更加确实地加以接受。英国伯明翰大学的Kirill Ilinski使用了费因曼的量子电动力学理论去模拟市场动态，与此同时还利用这些概念去重新推导Black—Scholes方程。Ilinski用一个所谓的套利场(它能描述选择权和股票价格的变化)去代替控制带电粒子相互作用的电磁场。(把股票和选择权有价证券协调起来的交易称为套利。)

Ilinski的理论证明了量子动力学能够怎样去模拟Black、Scholes和Merton的海静方法，在海静方法中，市场动态决定了一个股票的任何收益将被选择权价值的下降所抵销，从而产生一个无风险回报。Ilinski把它比作“虚拟粒子(即光子)的吸收。这种吸收使两个电子之间的相互作用力衰减。他接着证明他的套利场模型如何能解释获利机会，而在Black—Scholes的原始方程中却没有涉及到这一点。

Ilinski是刚开始形成的经济物理学领域中的一员，经济物理学去年7月在布达佩斯举行了它的第一次大会。然而，在物理和金融之间字面上的类似没有赢得几位拥护者。法国的投资银行Paribas的一位资深顾问、经验丰富的衍生产品交易商NasslmTaleb指出：“它并不符合在科学和空谈之间十分简单的区分原则。”Ilinski认识到他的工作存在着矛盾。他苦笑着说：“有些人接受我的研究结果，有些人说我疯了，因此，存在着观点分歧。”

无论求助于RichardFeynman或FischerBlack，利用数学模型去估价海静证券都是一种估价实践。“模型风险”这一术语描述了对于一种衍生产品来说，不同的模型能产生大为不同的价格，而当它们不同于一种金融工具能在市场上被买卖的价格时，这些价格又会造成巨大的损失。

模型风险以许多形式出现。一种模型的复杂性能造成对衍生产品的错误估价。在模型背后的不正确假设也能如此——例如，在一次汇率危机过程中未能考虑到利率的易变化性。许多模型未能充分妥善处理市场变量之间关系会发生的突然变化，例如美元与印尼盾之间正常交易范围的变化。纽约市一家评估模型完整性的公司——资本市场风险顾问公司的负责人Tanya Styblo Befler说：“模型或你使用模型的方法并没有抓住正在发生的事情。情况在变化。好像你在一条非常陡的路上往下开车，你认为你正骑在一辆自行车上往下滑行，但你发现你所坐的却是一辆没有刹车的牵引拖车。

按需定做的金融工程产品并不在公共交换票据上进行交易，因此要依赖于由模型产生的定价，有时候就很难与市场上其他金融工具比较模型的定价。当出售的时机来临时，市场可能报出一个与模型所估价格大为不同的价格。在某些情况下，一位交易商可以利用另一位交易商的模型中可能出现的错误定价而卖出一份被过高估价的选择权来获利，这种做法称为模型套利。

在摩根·斯坦利公司开发和试验固定收益证券的前数学家Jose．phA．Langsam说：“存在着盲目接受一些模型的危险。摩根·斯坦利公司和其他一些企业接受了各种试验方法，如确定他们的模型在估价价格已知的衍生产品时的正确程度的方法。

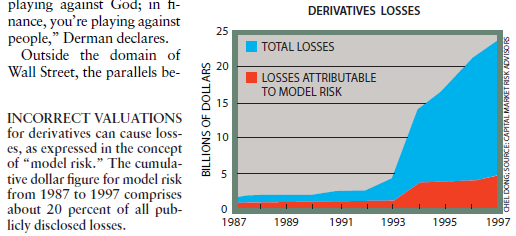
据资本市场风险顾问公司的介绍，与模型有关的问题在过去十年中大约占到237．7亿美元的衍生产品总损失中中的大约20%。但是在去年，模型风险占到26．5亿美元的损失中的几乎40%。1997年的损失数中包括国家西敏银行的1．23亿美元和瑞士联合银行的2．4亿美元.

二月份由《衍生产品战略》杂志赞助的一次会议就“首先消灭所有模型”的议题举行了一次圆桌讨论会。有些与会者提出，最复杂的那些数学模型是否能与交易商的技巧和对于市场动态的直觉相匹敌，纽约市FIMAT总会衍生产品交易部负责人Stanley R．Jonas说：“随着模型变得越来越复杂，人们将使用它们，于是它们就变得很危险，因为使用它们的方法对于经济健康是有害的。由伦敦商学院的Jens Carsten Jackwerth和加利福尼亚大学伯克利分校的Mark E．R．ubinstein所作的一份未经发表的研究显示，交易商凭自己经验推断未来股票指数的波动情况要胜过许多重要的模型方法。

在这次讨论会上，有一位模型研究者一Goldman Sachs公司的Derman站出来捍卫自己的成就。他宣称：“让我意译毛泽东在六十年代的一句名言：百花齐放。他把模型与思想实验作比较，思想实验是非经验的，但有助于物理学家更清晰地对世界进行思考：“爱因斯坦会思考坐在以光速运动的波浪的边缘将会怎样，并会看到什么东西。我认为我们正在做着类似这样的事情。我们正在探索着想象中的世界，试图从中获得一些有价值的东西，看看哪一样东西与我们的现实世界最相似。Derman承认，每个模型都是不完善的：“你需要思考如何解释模型与现实世界之间的不相吻合之处。”

金融氢弹

受到广为传播的一些金融崩溃事件的影响，衍生产品的形象被玷污了，这些事件中包括巴林银行的破产，加利福尼亚州奥兰治县的破产，宝洁公司的巨额亏损和Gibson礼品公司的巨额亏损。人们引用投资银行家Felix Rohatyn对二十来次计算机黑客事件的危害性的警告一一“金融氢弹”。有些企业和地方政府已经完全从他们的有价证券中清除了衍生产品：甚至出现了对整个金融体系出现一次大毁灭的担忧。

这些新奇金融工具的创造者们则把这些损失放到了更宽阔的视野中来看待。按照国际清算银行的资料，选择权、期货、远期和互换交易合约所由之衍生的所有股票、债券、通货的理论值(即面值)，在1995年总计为56万亿美元。待履行的衍生．产品合约本身的市场价值只占总数额的百分之几，但其数量仍然总共可能有几万亿美元。相反，从1987年到1997年，已知的衍生产品损失总共只有238亿美元。更为普通的投资也能伤害投资者。当利率在1994年猛涨时，库存公司债市场损失了2300亿美元。

衍生产品之所以能造成新闻是因为，就像一次飞机失事那样，它们的损失是突然的和剧烈的。合约可能涉及到巨大的杠杆作用。一位衍生产品投资者可以只投入其背后的资产(一种股票或一种债券)的很小一个份额。该资产的价值的一个很小的百分比的变化却能产生该衍生产品价值上的一个很大百分比的收益或损失。

为了驾驭拥有衍生产品和其他证券时的风险，金融机构会从另一些数学模型中去寻找庇护。许多这种做法是源于1990年诺贝尔奖金得主Harry M．Markowitz所据出的有价证券理论，这是一种统计计量和优化方法。他就是因这一理论而获奖的。Markowitz阐明了投资者怎样对一个给定水平的回报来使风险达到最小，其方法是让资产多元化，当市场变化时，这些资产不会都以相同的方式作反应。

Markowitz的一件常用工具称为风险中的价值(value at risk)。它采用一组技巧，它们引出了单独一个投资损失最坏情况数字。风险中的价值要计算现有的每一种有价证券(从通货到衍生产品)的最大损失概率，然后得到该公司整体金融资产所面临的一个风险中的价值：最严重的情况是在今后30天中以给定的统计置信区间所能预期的损失有可能达到8500万美元。对有价证券的一次分析显示了风险集中在什么地方。

加利福尼亚大学欧文分校的金融教授Philippe Jorion作了一个实例研究，它显示风险中的价值法如何能对即使是不老练的投资者来说也会发生必要的警告。如果投资于县基金而损失了17亿美元的奥兰治县教委成员知道有5%的可能会蒙受10亿美元损失，很可能就会换一种做法了。

就像其他模型方法那样，风险中的价值方法也招来了对它如何预测真实世界中涨跌的能力的怀疑。使用得最广泛的计量技术严重依靠历史上的市场数据，这些数据未能反映罕见的但又是极端的事件的重要性。位于多伦多市的一家风险管理软件公司一一算法公司的总裁Ron S．Dembo评论道：“如果你采用去年的数据值，你可能看到一种有价证券只有10%的变化。随后，如果你再往前移动一个月，事情可能发生100%的变化。”算法公司和其他公司从最简单的风险中的价值法向前推进了一步，他们向银行提供的软件能够对一种有价证券作出“应力试验”，其方法是模拟市场大起伏的影响。

一种模型方法可能派生出另一种模拟方法，而市场崩溃肯定将按照它们内在的价值继续发生。但是，把价格置于不确定性之上的能力(这是金融工程的精髓)已经证明了它在其他业务环境以及在政府决策和国内财政中的价值。选择权理论能够有助于资本投资的运作。一种传统的投资分析也许会建议，一家电力公司最好投资建设一座其发电能力能满足10到15年的需求增长的大型燃煤电厂。但是这一方法有可能牺牲了建设一系列小型燃油电厂的方案，而如果需求增长比预期要慢得多的话，后者却是一个更佳选择。选择权定价技术能够把一份资产放到缓慢增长道路所提供的灵活性上。

Black—Scholes模型还被用于定量评估一个发展中国家为工人提供普遍的教育而不是以培训特殊技能为目标所带来的利益。它揭示，随着经济转型而能迅速改变劳动技能的价值能超过提供普遍教育所花费的额外成本。选择权定价甚至能用来评估选择一位“计划之外”的医生来承担管理保健的灵活性。诺贝尔奖得主Merton说：“这一方法的意义不仅仅在于直接金融市场，而且还能用于如何组织非金融企业，以及人们一般如何组织自己的金融生活。”把一笔资产投向变幻莫测的未来可能有助于实现另一位诺贝尔奖得主的想法：斯坦福大学的Kenneth J．Arrow设想有一种能对付世界上每一种情况的手段——而每一种风险(从破产到雨中野餐)都能转嫁给他人。

图1 Goldman Sachs公司的Emanuel Derman是由物理学家改行而担任金融工程师的。他手持一幅“树”模型图，用此图证明股票指数价格的反复无常。

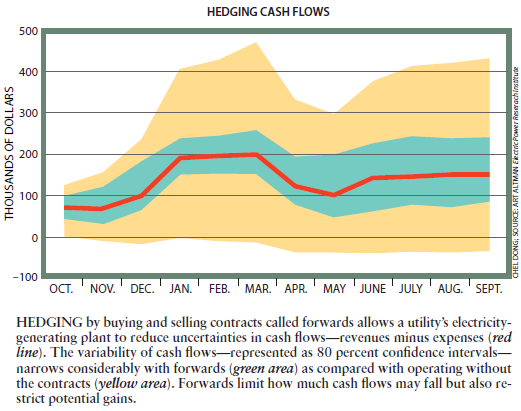
图2通过买卖称为期货的合约，海静(有风险消平的意思)允许一家电力公司的发电厂减少现金流动——收入减去开支(红线)——中的不确定性。与没有合约的运作(黄色区域)相比，现金流动的可变性——以置信区间80%表示——因期货而显著变窄了(绿色区域)，期货限制了现金流动能降低多少；但也限制了潜在的盈利程度。

图3麻省理工学院的斯隆管理学院中所开设的“定量学校”在一间建造得象交易厅的教室里向学生们讲授金融工程理论中的微小差别。

图4对衍生产品的不正确估价能导致损失，正如“模型风险这一概念所表达的那样。从1987年到1997年模型风险所累加起来的美元数占到了所有公布的损失的大约20%。

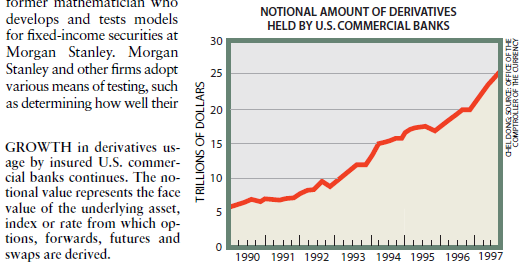
图5美国投保的商业银行所使用的衍生产品继续增长。全国总额代表了衍生出选择权、期货、远期和交易的资产、指数或利率的面值。

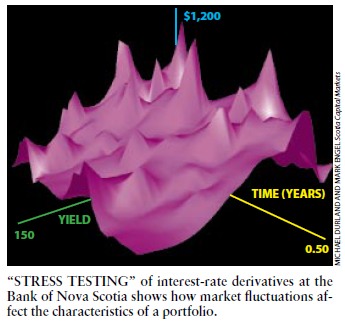
图6新斯科舍银行对于利率衍生产品所作的“应力试验(stresstesting)”显示了市场的起伏如何作用于一种有价证券的性状。