互动科普

我们在通常谈话中说到某件事情不可能时，我们的意思常常并不是指“它真的不可能”，而是说我们还看不到有什么办法以解决这件事情。以前许多人曾认为比空气重的机器飞起来是不可能的，而更早之前还有许多人认为比水重的机器要浮在水上是不可能的。但人的智慧不断地克服了这些乍看起来似乎是不可能的事情。

然而，在数学上，“不可能”却常常是可以证明的事情。例如，3不可能是2的整数次幂。证明这件事情的一个办法是找出2的多少次方可能等于3。此时你将发现用l作指数太小(21=2)，而用2作指数又太大(22=4)。但是，关于不可能性的证明仅是在现在已经确立的数学体系内才起作用；如果你改变游戏规则，情况就可能发生变化。例如，在“模5”的整数集中，5的倍数被看作0，而超过5的数都要转化为用5来除它后所得的余数。当然这并不意味着我最初那个关于不可能性的证明是错的，因为问题的前提已经改变了。这个例子的意思仅仅是说，我应该更加谨慎地定义我所讨论的问题。

数学能够证明某些事情不可能，这种能力具有某种令人失望的副作用。想象一下我花了过去十年在一本又一本的笔记上写满计算，并确信我已经发现了一个有几千位长的新素数。不过，与其它任何已知素数不同，这个素数是偶数。它的最后一位数用通常的十进数表示就是6。这个令人惊异的成就使我激动得无法形容，于是我把这项成果寄给了一位数学家。不料这位数学家马上就把它退还给了我，并对我说这完全是一派胡言。更气人的是，当我请他指出我究竟错在何处时，他却说他根本没有读过我的研究成果，因此不知道错在哪里，但他知道其中必定有个错误。这位数学家的傲慢武断令我感到吃惊。

在大多数日常生活的圈子里，这位数学家的态度算得上傲慢武断。但是在数学中，这只过是稍稍用了点逻辑推理而已。唯一的一个偶素数是2。不存在其它任何偶素数。

最深刻的不可能性定理之一是由两位数学家——挪威的Niels Henrik Abel和法国的Evariste Galois——在十九世纪初各自独立地引入的。他们各自运用不同的方法证明了一般的五次方程不能够用只含有通常的代数运算和开方运算(即开平方、开立方、开四次方等等)的公式来求解。在此之前数学家们已经发现了用根式求解复杂程度低一些的方程的方法：二次方程可以用人们熟悉的求根公式来求解，三次和四次方程也有类似的公式。但是人们想尽种种方法来寻找五次方程的求根公式均未获成功。Abel和Galois证明了这类尝试永远不可能获得成功，从而使人们自此后放弃了这类徒劳无益的尝试。

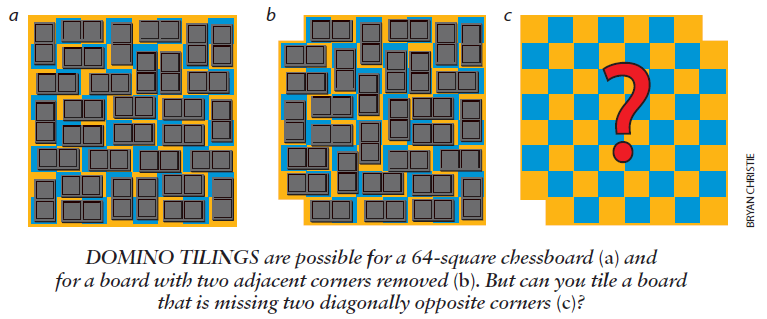
为了看出为什么能够作出这类证明，试考虑一个著名的难题。国际象棋棋盘有64个方格。如果你取32个多米诺骨牌来，每个骨牌都由其大小与棋盘上的方格相同的两个方块构成，则把这些骨牌铺满整个棋盘的方法有许多种。如果你去掉棋盘上相邻的两个角，你可以很容易用3l块骨牌来铺满剩下的棋盘。但是，如果你去掉棋盘的对角方向上的两个方格，那么无论你怎样尝试用骨牌来铺满剩下的棋盘也不会成功。

你屡试屡败是不是就证明了这个问题是不可能解决的呢？否。即使你用了一辈子的时间来尝试也没有取得成功，仍然不等于你证明它属于不可能解决的问题。铺满上面提到的最后一种棋盘是不可能的事情吗?是的，而且我们可以证明它。如果你把一块骨牌放在棋盘上，它总是占据一个白色方格和一个黑色方格。这样，如果你要用骨牌来铺满一个棋盘，这个棋盘的黑色方格和白色方格的数日就必须相等。对于上面提到的头两个棋盘来说，情况正是如此；但对于对角方向上的两个方格被去掉的那个棋盘来说，情况就不是这样了。这个棋盘的两种颜色的方格数目分别为30个和32个。

这个证明的基本要素与Galois证明五次方程不可能用根式来解时所使用的基本要素是相同的(Abel的证明不能恰好用这一方法来概括)。两种证明都涉及到引入某种不变量，也就是我们即使不知道假设的解的具体形式也能够计算出来的这个解的某种特征。对于骨牌铺砌问题来说，不变量非常简单，即黑色方格和白色方格的数目必须相等。而对于五次方程来说，不变量就是方程的根的对称性的某种复杂代数结构，称为Galois群。如果不变量与问题的条件不一致，则不管提出什么样的解肯定都是错误的。我们甚至看都不用看一眼这个解就知道它肯定行不通!

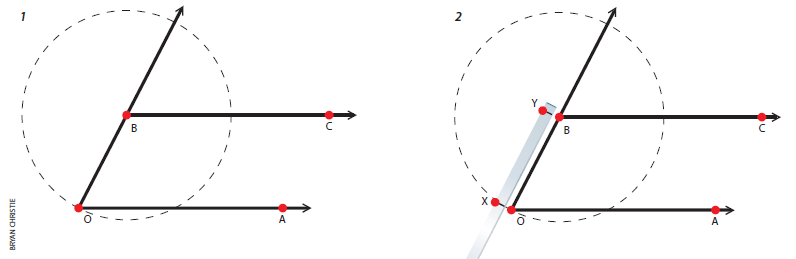
类似的不可能性定理还可以在另一个流行的游戏数学领域——儿何作图——中发现。在最简单的几何作图中，只允许使用一把无刻度的直尺和一只圆规。作图从一组已知的点开始，通过直线相交或圆的相交一步步得出新的点。所作出的任何直线都必须把已知点连起来，而任何圆的圆心都必须在已知点上并经过另外一个已知点。

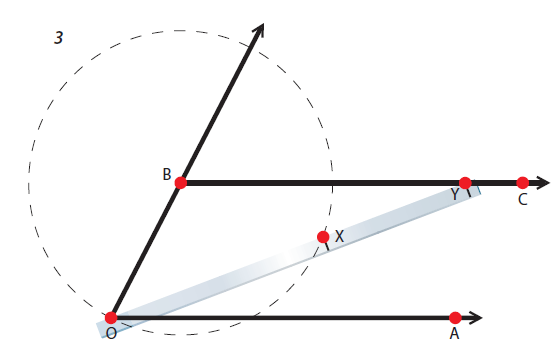
利用上述作图规则可以解决哪些数学问题呢?你可以把给定的一条线段分为任意数目的相等线段。你也可以把给定的一个角分为相等的两个角——也就是平分这个角，而且，把平分一个角的方法反复地用几次，你就可以把一个角分为2n个相等的角。你还可以画出其边数分别为3、4、5、6、8、10和l2的正多边形。所有这些知识早在欧几里得时代就已经知道。在其后的两千年中，许多数学家试图用同样的问题：倍立方体问题，即作一个立方体，使其体积等于己知立方体体积的两倍。三等分角问题，即把一个已知的角分为三个相等的角。化圆为方问题，作一个正方形，使其面积等于已知圆的面积。现在我们知道为何数学家们费尽九牛二虎之力也无法解决这些问题了：所有这三个问题都是不可能用圆规直尺作图法来解决的。

我们这里寻求的是精确的解，而非近似解。这三个问题用近似方法来解决是很简单的，而且可以达到所要求的任意精度。此外，除了无刻度的直尺和圆规外，我们能使用其它任何工具。如果允许使用有刻度的直尺，那么三等分一个角就很容易了。

圆规直尺作图的不变量是什么呢?任何这类作图都可以用坐标形式来表示，从而化为对一系列的数——即相关的各个点的坐标——进行计算。作图过程中的每一步都产生出若干坐标，它们可以用一个一次方程或二次方程与已知的坐标联系起来。(一次方程相应于直线与直线相交的步骤，二次方方程相应于涉及到圆的作图步骤。)这就意味着作图中的任何一点的“次数”——以该点为其解的次数最低的方程必须是2的幂。这是圆规直尺作图的最简单的不变量，只要有这个不变量就足以证明上面三个作图问题是不能解决的了。

倍立方体问题等价于解方程X3-2=0，而这是一个三次方程。由于3不是2的整数次幂，因此使用圆规直尺作图法不可能把立方体的体积扩大一倍。三等分角问题也等价于解一个三次方程(这可由三角学和公式COS3X=4(COSX)3—3cosx推出)。因此这个问题也不可能解决。

化圆为方问题等价于求解一个被π所满足的二次方程。但是，根据十九世纪德国数学家Ferdinand Lindemann证明的一个定理，π不可能满足任何这类方程，因为π不能够用有限多的代数运算来表示。

这样我们就知道了任何人想要仅凭没有刻度的直尺和圆规来解决这三个作图问题都完全是白费功夫。然而，尽管已经有了这类问题根本不可能解决的证明，却常常无法阻挡一批又一批人去作解决这些问题的徒劳无益的尝试。Underwood Dudley写了一本引人入胜的书，书名叫“三等分角的狂热信徒”(The Trisectors，美国数学学会1994年出版)，叙述了许许多多这类枉费心机的尝试。遗憾的是，试图用无刻度的直尺和圆规来三等分一个角同试图证明3为2的整数次方一样是毫无意义的。

顺便说一句，请所有热衷于三等分角的人注意，出于上面已讲清楚原因，所有这类尝试一律不会在本专栏的“反馈信息”栏目中发表。请寄给专门收集这类尝试的Woody Dudley。但是我愿意知悉三等分角的巧妙工具，或者是特别漂亮的近似作图法，因为我知道这些是能够实现的。