互动科普

Jackson Pollock发明了一种新技术，在水平帆布上倾倒连续的颜料流，以产生一种独特的连续线条。1994年我决定暂停我的科学生涯去绘画。在一次暴风雨天气里，我们提出让大自然帮我们绘画的主意。

我们收集树枝，搭建一个大装置。装置的一部分起着吸收风力的大风帆的作用，然后将风力传递给带颜料罐的另一部分，这样罐中的颜料就会在地面的帆布上滴洒一种与风的运行路线相对应的图案。当又一场大风暴开始袭来时，我们决定撤回室内，让该装置留下来整夜作画。第二天，风暴过去了，但它留下了一幅类似Pollock所作的画！

突然，我想到了Pollock的秘密：他一定在作画时采用了大自然的韵律。这时，我意识到必须重新开始科学研究，以确认能否在他的作品中找到这种韵律的实质性踪迹。

艺术期待科学

在Pollock的时代，自然界被认为是无序的，本质上是随机运动的。不过，从那时起，出现了两个引人注目的研究领域，使人们对自然界的规律有了更深的理解。

在20世纪60年代，科学家开始考察自然界的系统(例如天气)如何随时间而变化。他们发现，这些系统并不是随意变化的，其背后潜藏着一种可察觉的微妙秩序。他们将这种状态称为“混沌”，并发展了一个称为“混沌理论”的科学新领域，用以解释自然界的动力学。后来在20世纪70年代，出现了一种描述混沌运动留下的图形的新型几何学。图形的发现者Benoit Mandelbrot将这些图形称为“分数维形”(fracta1)，它们与传统的欧几里德图形毫无相似之处。与人工画的直线相比，分数维形包含许多放大看会重复出现的越来越小的图形，它们共同构成极为复杂的图案。由树枝完成的新型绘画提醒我：Pollock绘画作品中看似随机的曲线可能包含某种微妙的秩序，他的作品很可能就是分数维形。

分数维形的一个关键特征是具有分数维度D，该维度量化了不同放大倍数下各图形间的比例关系。对于欧几里德图形来说，维度是一个用熟悉的整数值来描述的简单概念。对于一条不含分数维形结构的直线，D值为1；对于一个完全填充的区域，D值为2；然而，对于一个分数维形，重复的结构使线条占据了一定的区域，这时D值介于1和2之间；随着重复性结构的复杂性和密集度的增加，D值不断趋近于2。

为了搞清楚Pollock在绘画中是如何运用分数维形的，我重新回到新南成尔士的实验室，借助于计算机对Pollock在帆布上的画作进行量化研究。如果没有计算机提供的精确性和计算能力，要完成这种分析是不可能的。因此，我聘请了两位计算机专业的同事，一位叫Micolich，他正在为获得半导体设备方面的博士学位而进行分数维形分析技术的研究；另一位叫Jonas，他是一位图像处理技术专家。

我们首先把Pollock的一幅画扫描进计算机[见下页图文]；然后，将计算机生成的由众多相同正方形组成的网格覆盖在画上。通过分析哪些正方形被绘画作品填充，哪些没有被填充，我们可以获得绘画作品的统计学数据。通过缩小正方形的尺寸，我们能够以更精细的比例研究它。我们分析研究的作品，包括尺寸从最小的颜料斑点到1米见方的绘画作品。令人惊异的是，我们发现这些画都是分数维形，不论其尺寸大小——最大作品的尺寸是最小的1000多倍。实际上，距这次发现的25年前，Pollock就已经开始创作分数维形绘画作品。 

分数维形的美学魅力

进一步，面对这个惊人发现，我想：是否分数维形的特征增添了Pollock绘画作品的魅力呢?只是在过去的10年里，研究人员才开始研究分数维形的视觉优点。利用计算机生成的各种D值的分数维形图案，IBM公司的Watson研究中心的A. Pickover发现，人们偏爱那些D值为1.8的分数维形图案。而成斯康星—麦迪逊大学的J. Aks和C. Sprott通过不同的计算机方法生成的分数计算机分析和照片研究证明了这是一种非常系统而认真的绘画程序。Pollock首先画出散布于帆布上的局部“小岛”。这是很有趣的，因为自然界的某些图案始于微小晶核。然后是晶体的扩展与合并。他接下来画出连接各“小岛”的更长的延长线，这些线条逐步被致密的颜料分数维形网络所掩盖。绘画在这一阶段形成了一个底层：它实际上将指导画家下一步的创作行为。在连结“小岛”的过程中，作品的复杂性(D值)在不到1分钟的时间里激增。在完成了这一快速的创作之后，Pollock会休息一下。然后，他重新回到帆布旁，在接下来的2天至6个月不等的时间内，他将在黑色底层的上面用不同颜色的线条叠加更多的画层。基本上。他在这段时间是对底层确立的复杂性进行微调。即便是在绘画工作完成之后。Pollock还要采取步骤来使作品的分数维形特征最大化，例如剪掉那些分数维形质量不佳的边缘区域。

维形的研究得出，人们偏爱的D值为1.3，比Pickover的结果低得多。这一差异也许表明，没有哪种D值比其他D值更优越。分数维形图案的美学品质取决于它们的产生方式——我质疑一种人们普遍偏爱的D值的存在。

为了验证我的看法，我再次求助于专家——这次求助的是从事视觉感知研究的心理学家。他们分别是新南威尔士大学的Spehar，现任职于悉尼大学的Clifford，以及伦敦大学学院的Newell。在他们的帮助下，我对3类基本的分数维形图案进行了研究，它们分别是：自然类(如树木、山脉和云层)、数学类(计算机模拟图案)和人文类(Pollock绘画作品经裁剪的部分)。在视觉感知测验中，受试者一致对D值在1.3至1.5范围内的图案表示偏爱，而与图案的来源无关。最近，我又与华盛顿州立大学的心理学家Wise进行合作，我们研究发现，这种视觉偏爱对观察者的心理有一定影响。我们通过皮肤电导测验对受测者的紧张程度进行了测量，结果表明，范围居中的D值使人们放松——当然，这些研究才刚刚开始。尽管如此，令人感兴趣的是我们周围自然环境的许多分数维形的D值就落在这个范围内，如云层的)值为1.3。

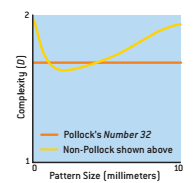
Pollock作品的D值是多少呢?意思的是，在他创作滴画的10年里，其作品的D值是不断增加的，从1945年的1.12增加到1952年的1.7，一幅被Pollock毁弃的作品中，其D值甚至达到了1.9。尽管人们偏爱低范围的D值，但Pollock却花了10年的时间改进他的滴画技术，以创作出高D值的分数维形作品，这一点令人费解。不过，高D值作品不断增加的复杂性可能比居中范围D值的“放松性”图案更能吸引观众的注意，因此可能对画家产生一种内在的吸引力。我目前在俄勒冈大学的工作就是验证这种可能性，我利用视点跟踪仪，研究人们观看分数维形图案和Pollock绘画作品的方式。

显然，利用计算机技术研究绘画作品的本质特征为艺术史家和理论家提供了一种有效的新工具。计算机技术将与艺术家业已常用的红外、紫外和X射线分析一起，成为研究某些艺术作品(如隐藏在颜料下面的绘画)的日益广泛的科学手段。计算机技术也许会成为一束照亮画家心灵深处的光，那里正是伟大画家的力量源泉之所在。