互动科普

计算机的功能只是在最近才强大到足以阐明湍流这一重大的经典问题的若干简单例子。在某些情况下，计算机将使工程师能控制湍流。

我们的生活无处不碰到流体的流动，甚至就是靠流动来维持的。血流经我们体内的血管，空气(严格说来是一种流体)则被吸进我们的肺中：我们的交通工具在大气层中或注湖泊和海洋上行驶，而它们的动力则是由另一些在发动机的燃烧室中混合的流体（如燃料和氧化剂等）提供的。事实上，如果没有对流体力学的透彻了解，我们是不可能对付今天所面临的许多环境问题或与能源有关的问题的。

令科学家与工程师感兴趣的几乎所有流体运动都是湍流；湍流是流体动力学中的常规而非例外。例如，有了对湍流的可靠认识，工程师们就能够设法减少汽车或民航客机所遇到的气动阻力，提高喷气式战斗机的机动性能或改进发动机的燃烧效率。为了全面掌握血在心脏中的流动情况——特别是在左心室的流动情况，该处血的运动特别迅速——湍流的知识也是必不可少的。

但湍流究竟是什么呢?几个日常生活中的例子或许有助于说明问题。把厨房的水龙头稍微拧开一点，水便从龙头中平稳地流出。这种流动称为层流：把龙头再开大一点，水流便开始动荡并呈波状，换言之也是成了湍流。当烟雾从一根燃着的烟上飘进平静的空气中时，也可以观察到同样的现象。紧挨烟头上方的烟雾呈层流状再高一点，烟雾就成了波状并扩散开来。

湍流是由涡旋构成的：涡旋就是曲折的，常常是盘绕的流动区域，此时流体无规律地绕着总的流动方向运动。用专业术语来说，当流体的速度超过了某一特定的阀值时，流体运动就会进入这种混沌状态；而低于这一阀值时，粘性力就抑制了混沌行为。

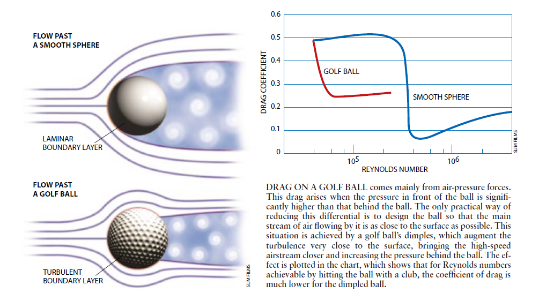
然而，湍流并不只是一种人们一见到它就必欲除之而后快的有害现象。情况远非如此:相反，许多工程师还在绞尽脑汁设法加强湍流。例如，在内燃机的气缸中，湍流可使燃料和氧化剂的棍合更彻底。从而产生更洁净、效率更高的燃烧。此外，也只有湍流能够解释为什么高尔夫球上的凹点能够使一个高尔失球老手把球打出250米远而不是最多100米远。

湍流之所以名声不好，其原因可能是湍流的数学处理是经典物理学中最有名的棘手问题之一。对于这种真正说得上是无处不在的现象来说，迄今对它的定量特性的认识实在是少得出奇。杰出的诺贝尔奖获得者、物理学家Richard Feynman称湍流是“经典物理学最重要的未解决问题”。1932年英国物理学家Horace Lamb在向英国科学促进协会致辞时十分幽默地点出了这个问题的难度。据报道他是这样说的：“我现在老了，当我死后去见上帝时，我希望有两件事他能替我指点迷津。一件是量子电动力学，另一件是流体的湍流，对于前者我持相当乐观的态度。”

当然，Lamb不可能预见到现代超级计算机的发展，这些技术奇迹终于开始使工程师和科学家们有可能获得对湍流短暂然而宝贵的认识。这方面的研究所孕育出的正在开发中的技术有朝一日可能用于飞机机翼上，使气动阻力降低百分之几。这足以节省成百上千亿美元的燃油成本。同时，对湍流的这些认识也在指导着喷气发动机的设计，提高了发动机的效率并改进了性能。

对湍流的研究尽管高深莫测，但它只是流体动力学这一更大领域(它研究所有液体和气体的运动)的一个重要组成部分。类似地，应用功能强大的计算机去模拟并研究恰好属于湍流的流体运动也是计算流体动力学((CFD)这一新兴领域的一个重要组成部分。最近几年中，流体动力学家已运用超级计算机模拟多种情况(如美洲杯帆船赛和血液在人工心脏中的流动)中的流体运动。

酝酿了150年的计算流体动力学

所谓用计算机来模拟流体的流动是什么意思呢?简单地说就是用计算机来解一系列著名的方程，这些方程用于计算流体绕着一个物体流动时该物体周围空间任一点上的流体速度和压力。这些方程是一个半世纪多以前由法国工程师Claude Navier和爱尔兰数学家George Stokes各自独立地发现的：由牛顿运动定律直接导出的这些方程称为Nevier-Stokes方程。计算流体动力学这一领域正是把超级计算机用于这些方程后的产物。Navier- Stoke，方程与超级计算机的结合是这些方程本身建立之后流体力学中的最伟大的成就之一。

虽然这一联姻得以大功告成，但求婚却是一个相当长的过程，直到六十年代后期，超级计算机的处理速度才逐渐达到了快得足以解出某些相当简单的情况下的Navier-Stokes方程的水平(例如绕着一个障碍的二维低速流动)。在那之前，风洞基本上是检验新型飞机设计的空气动力学特性的唯一手段，甚至是现在，功能最强大的超级计算机的局限性仍然使工程师们必须依靠风洞来检验新型飞机的设计。

虽然目前计算流体动力学和风洞两者都用于飞机的研制工作，但计算机技术和算法的持续进展却正在使计算流体动力学在这一过程中占有越来越重要的地位。在工程师们确定飞机的关键尺寸及其它基本数据的早期设计阶段，情况尤其是如此。试错法在这一过程中占据着

统治地位，且风洞试验的费用非常高昂(它要求设计人员建造一连串模型中的每一个并对其进行试验)，由于计算流体力学所起的作用越来越大，一个典型的设计周期现在需要对翼型进行2到4次风洞试验，而不是以前曾被定为标准的10到15次试验。

非常有趣的是，超级计算机模拟的另一个优点是它能够模拟更逼真的飞行条件。风洞试验可能因风洞壁和飞机模型支架的影响而失真。某些未来的飞行器其飞行速度将超过音速的许多倍，且它们所遇到的极端条件是风洞试验无法实现的。对于高超音速飞机(其飞行速度

可达音速20倍的飞机)和既在大气层内、也在大气层外飞行的空间飞行器，计算流体动力学是唯一可行的设计工具。对于这些要穿过薄薄的最上层大气的飞行器，必须考虑非平衡态空气化学和分子物理学。

发动机设计人员也广泛使用计算方法，特别是在研制喷气发动机时。一项称为“综合高性能涡轮发动机技术”的研制计划正在争取到2003年时使喷气发动机的推力——重量比提高百分之百，而燃油效率提高百分之四十。这个计划由美国国防部、国家航空航天局和各喷气发动机制造商提供资金。

空气和燃料穿过一台喷气发动机的各个部分和各条通道的流动是很复杂的。一台风扇把空气吸入一个称为压缩机的内室，压缩机是多级的，其旋转和固定的各级使压力增加约20倍。这一高压空气被送入燃烧室中，在那里与燃料混合后被点燃。最后，高度膨胀的炽热排气驱动一台涡轮机。此涡轮机提供驱动风扇和压缩机的动力，而更重要的则是引导排气从发动机的后面高速喷出，从而产生推力。目前，工程师们应用计算流体动力学来设计涡轮叶片、入口通道和燃烧室的几何形状模拟也有助于工程师们设计加力燃烧室混合器。(在军用飞机上，加力燃烧室产生额外的推力以使飞机具有更大的机动性。)此外，在设计短舱时，模拟也起着一定作用。(短舱就是通常挂在机翼下方的短粗的圆筒形发动机外壳。)

应用方程

为了理解Navier-Stakes方程的用处，试考虑一下空气沿一架飞行中的飞机的流动情况。事实上，计算机的功能强大到足以详细模拟流体沿整个飞机的流动情况可能是几十年以后的事了。然而，从理论上说，根据Navier-stokes方程可以得知空气在流经飞机表面附近任何一点时的速度与压力。然后工程师们就可以利用这些数据来算出各种飞行条件下的所有有用的空气动力学参数，即作用于飞机上的升、阻力和扭矩(扭转力)。

阻力是特别重要的，因为它决定了飞机的燃油效率。对于大多数飞机，燃料成本都是最大的运营费用项目之一。各飞机公司耗费巨资来降低阻力，以设法争取哪怕是点滴的改进，这是毫不令人奇怪的。不过，一般说来，升力比较容易计算，扭矩次之，而阻力则是最难对付的。

阻力之所以难于计算主要是因为它是与湍流关系最大的参数。当然在这种情况下，我们并不是指的那种促使驾驶员提醒乘客注意系好安全带的颠簸。即使一架飞机处于平稳的飞行状态，在距飞机表面几厘米这一范围内(称为边界层)的空气的流动仍属于湍流。由于湍流的缘故，机翼表面上方几毫米处的高速空气被带到极为接近表面的地方，在此处它经历了更急剧的减速(同时还失去了动量)。与这一流动减速作用的大小相等而方向相反的反作用就是飞机所受到的阻力了。空气动力学家们的大量研究工作都是为了充分认识湍流的产生及破坏的机制，以便能控制它。

为了解出Navier-Stoke方程，工程师们第一步是把某些变量〔称为初始条件和边界条件)输入方程中。对于一架飞行中的飞机，初始条件包括风速和大气扰动(如气流等)。而边界条件则包括用数学坐标表示的飞机精确形状。

在把方程应用于飞机之前，计算机专家必须把飞机表面及其周围的空间表示成一种可由计算机处理的形式，也就是把飞机及其周围的空间用一系列规则分布的点(称为计算网格)来表示，然后他们把网格的坐标和其它相关参数输入把Navier-stokes方程用于这些数据的软件中。对于每一个网格点，计算机都计算出有用参数——即空气的速度和压力——的一个值。

事实上，计算网格把计算问题在空间中划分开来(专业上的说法叫“离散化”)。计算的过程则是模拟时间的流逝每过一定时间进行一次计算，因而此模拟在时间上也是离散的。计算网格中的点越密集(从而数量就越多)，对点的计算越频繁(也就是间隔时间越短)，模拟就越精确，越接近实际情况。事实上，对于形状复杂的物体，甚至连定义表面和生成计算网格都是一个困难问题。

遗憾的是，输入初始条件和边界条件并不能保证得到解，至少对于现有的计算机以及可以预见的未来的计算机是这样。问题在于，Navier-stokes方程是非线性的；换言之，方程中的许多变量之间的关系是平方关系或更高次方的关系。这些非线性变量的相互作用产生出

范围很广阔的各种尺度，这可能使得方程极难解出。在湍流中，具体地说，涡旋尺寸的范围上下可相差1000倍或更多。还存在着其它一些使间题复杂化的因素，比如说整体相关性;该方程的性质使得一点上的流体压力与其它多点上的流动情况有关。由于问题的各部分互相之间存在着紧密的联系，因此必须在许多点上同时获得它的解。

令人讨厌的计算问题

前面的介绍阐明了流体动力学模拟的要点，但它没有考虑湍流；而缺少了湍流，对计算流体力学的作用及其局限性——的现实讨论将是没有什么用处的。湍流的复杂性大大地限制了我们对流体运动进行符合实际的模拟的能力。

定义湍流的最简单的方法或许是借助于雷诺数，这个参数简洁地刻划了流动。此参数以英国工程师Osborne Reynolds的名字命名。它表示流动的惯性力与粘性力之比，即相对重要性。(流动的惯性力的计算方法是以流体密度和其流速的平方之积除以该流动的一个特征长度。对于绕着机翼的流动，这个特征长度就是翼剖面宽度。)

较大的惯性力(相对于粘性力来说)有利于湍流，而较高的粘性则抑制湍流的出现。换言之，当雷诺数超过某一值时，湍流就出现。雷诺数正比于物体的尺寸和流体的流速。例如，空气流经一架巡航中的民航客机机身时的雷诺数为1亿左右。对于流经一个巧妙打出的快球的空气，雷诺数大约为20万，而对于在中等尺寸的动脉中流动的血，雷诺数为1000上下。

我们已经看到，湍流的一个突出特征是它由尺寸相差很大的许多涡旋组成。这些涡旋不断形成又不断分裂。大旋涡分裂成较小的旋涡，较小的旋涡又分裂成更小的旋涡，如此等等。当旋涡变得充分小时，它们便因粘性作用耗散为热。英国气象学家Lewis F, Richardson写了一首诗来描述这一过程:

大旋涡产生小旋涡，

消耗了它们的速度，

小旋涡产生小小旋涡，

最终出现了粘性。

为了对比如说空气流过一架飞机这种情况解出Navier-stokes方程计算网格必须划分得足够密，以分辨最小的旋涡。另一方面，计算网格又必须足够大，把整架飞机和飞机周围的部分空间也纳人网格中去。湍流中长度尺寸的差距一一最大旋涡尺寸与最小旋涡尺寸之比——可通过求出该流动的雷诺数的3/4次方来获得。这一比例可用来估计一个具有一定精度的模拟所需的格点数:由于有三维，因此该数与这个长度尺寸比值的立方成正比。这样，一次数值模拟所需的格点数与雷诺数的9/ 4次方成正比。换言之，如果雷诺数增大一倍，则模拟流动的网格中所需的格点数将增加差不多5倍。

考虑一架机身长50米、翼弦长度〔即机翼前缘到后缘距离)为5米的运输机。如果这架飞机以每秒250米的速度在1万米的高度上作巡航飞行，则为了以合理精度对表面附近的湍流进行模拟，需要大约1亿亿个网格点(1010个网格点〕。

这样多的网格点对计算能力提出了什么样的要求呢?根据现有算法及软件所进行的初步估算表明，即使用计算能力为每秒1万亿（1012）浮点运算的超级计算机来进行模拟，也需要几千年的时间才能算出一秒的飞行时间中的流动情况。这种“万亿次”的计算机目前还不存在，不过桑迪亚国家实验室的研究人员现在正尝试建造一台。它将比现有的功能最强大的超级计算机系统快10倍。

模拟的捷径

幸运的是研究人员无需模拟空气沿整架飞机的流动情况就能得出有用的信息——事实上，对整架飞机进行模拟所产生的数据大概比我们有必要知道的数据多得多。通常流体动力学家们只关心湍流对工程设计上有重要意义的量——如流体的平均流量对于飞机来说则是阻力和升力以及热传导的影响——而在发动机的情况下，设计人员感兴趣的可能是湍流对燃料和氧化剂的混合速率的影响。

因此，常常采用的做法是在湍流涨落的尺度上对Navier-stokes方程进行平均。这就是说在实践中，研究人员很少计算每个小旋涡的运动，而是对大旋涡进行计算。然后运用专门的模拟技巧来估计小旋涡对较大旋涡的影响。这一方法得出的模拟的平均流场比实际流动平滑，因此大大减少了模拟这一流场所需的格点数。

这一平均过程所要求的各种专门模型的复杂性相差很大，从简单的粘度增强系数到整个的附加方程组。所有这些模型都要求作一些假定，并且含有一些由实验得出的可调节系数。因此在目前，对平均化湍流的模拟实际上就是这些模拟使用的模型。

然而，随着汁算机的功能日趋强大，流体动力学家们开始发现，他们能够直接模拟更大尺度的湍流涡旋，从而使他们可以减小模拟的尺度范围。这些方法是湍流的直接数值模拟(它分解出所有各种尺度的运动)以及湍流平均化计算方法的结合。

多年来，气象学家们一直运用此策略的一种形式——称为大涡旋模拟来预报天气。在气象学上，大尺度湍流具有特殊的意义，因此在气象学的场合中比较大的涡旋一般都是整个地被模拟的。较小尺度的涡旋的重要性仅在于它们可能对大尺度湍流有影响，因此对它们仅是建立模型。最近工程师们已开始运用这些方法去模拟复杂的流体运动，例如内燃机气缸内气体的运动。

计算流体动力学当前的另一发展动向是直接地完全模拟比较简单的流动(如管道中的流动)，这也是靠了计算速度的增加才得以实现的。虽然这类流动比较简单，但对其中雷诺数比较低的某些流动的模拟却使我们可以获得对湍流本性的深刻认识。它们揭示了壁附近的湍流涡旋的基本结构及其对阻力的影响的复杂性。它们还提供了有用的数据，使工程师们能够验证或调整他们在实际模拟复杂流动时所使用的专门模型。

最近，想要索取这类数据的工程师和科学家的人数迅速增多，因此美国国家航空航天局艾姆斯研究中心已把大量数据存档以供他们查看。虽然大多数研究人员还没有对湍流进行直接模拟所需的计算设施，但他们却有足够的计算资源(如高效工作站)对存档数据进行检索。

从预测到控制

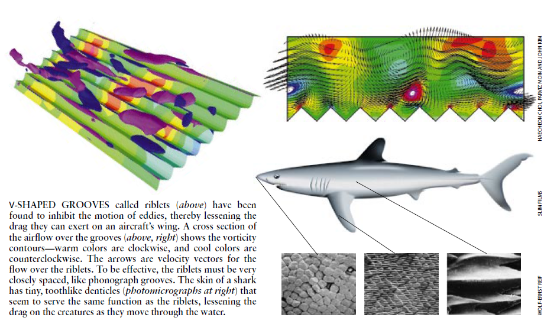
随着超级计算机的计算速度不断加快，流体动力学家们正在逐渐从只能预测湍流的效果发展到也能实际控制湍流。这类控制可以产生巨大的经济效益。例如，使民航飞机飞行时的阻力减少10%，可以使航空公司的利润增加40%。在最近的一个研究项目中，国家航空航天局兰利研究中心的研究人员证明，在飞机的机翼或机身表面放置一些纵的V形槽(称为“小肋”)可使粘性阻力降低5%到6%；虽然装小肋后与气流接触的表面面积有所增加，但阻力却下降。对于一般的运输机速度，小肋必须放置得非常密集，其间隔大约为40微米，类似于唱片声道。较大的小肋通常会使阻力增大。

在这项研究工作中，研究人员发现了苏联研究人员对鳖鱼皮上一类称为“小齿”的齿状结构的研究成果。这些小齿与小肋极为相似，人们认为这个事实是自然界对小肋概念的支持。然而，最终是靠了对沿小肋的湍流进行直接的数值模拟才揭示了小肋是通过防止涡旋进入离表面太近的地方(60微米以内)来抑制涡旋的运动的小肋把涡旋保持在这一微小的距离外，就使涡旋无法把高速流体输送到表面近处(在表面近处流体将减速并吸走飞机的动量)。

直接数值模拟最近的另一项激动人心的用途是用于研究主动式的湍流控制策略(而非小肋这样一类被动式的控制策略)。利用这类技术，可以使物体表面(例如机翼表面)根据流过其上的流体的湍流波动情况而发生轻微的运动。机翼的表面用合成材料制成，其中有数以百万计的埋置传感器和执行装置。它们根据流体压力和速度的变化而动作，以控制引起湍流阻力的小涡旋。   

就在3年前，这类技术似乎还是异想天开，然而，在美国空军的牵头下，微电子机械系统(MEMS)的进展已使这样一项方案发展到即将实现的地步。运用MEMS技术可制造出其上有必需的微传感器、控制逻辑和执行装置的集成电路对机翼表面附近的湍流的主动控制在海洋生物中也可以找到鼓舞人心的类比。海豚游泳的推进效率之高是引人注目的，流体动力学家们早就猜测这类动物是通过使皮肤运动而达到其高效率的。看来灵巧飞机蒙皮也得到了自然界的佐证。

现在回顾一下我们前面提到的高尔夫球:它们也是一个显示表面结构如何控制气流从而带来好处的令人感兴趣的例子（见图4）。高尔夫球所遇到的最重要的阻力来自与空气压力有关的力。这一阻力是因为高尔夫球前方的空气压力太大高于其后方的空气压力而产生的。由于高尔夫球表面的凹点造成湍流，它可以比其它方面完全一样但表面没有四点的球飞得远一倍半。

计算流体力学越来越普遍地用于研究湍流。既反映了它的前景终于开始得到实现，也反映了计算能力的持续的迅速增长。随着超级计算机的处理速度在未来几年中接近并超过每秒1万亿次浮点运算，流体动力学家们将开始着手解决雷诺数更高的更复杂的湍流。在下一个十年中，研究人员或许将模拟空气穿过喷气发动机中的关键通路的流动，并将实现对内燃机中的活塞一气缸总成工作状况的逼真模拟。包括燃料通过进气阀的吸人与燃烧以及通过排气阀的排出。通过这类模拟，研究人员最终将领悟到Navier-stokes，在一个半世纪以前发现的那些方程所包含的某些深奥秘密。

〔郭凯声 译 刘义思 校〕