互动科普

对小球和圆环抛接能力的研究使我们对人体动作协调、机器人学和数学有了新的认识。

为了完成递送军需品的任务，一位重148磅的男子必须走过一座既高且又吱嘎作响摇摇欲坠的桥，而这桥又只承受得起150磅的重量。可问题是他有3只1磅重的炮弹，并且时间紧迫，他只能过一次桥。这个古老的难解之谜的解是，这位男子一边过桥，一边用这3发炮弹玩起了杂耍。然而事实上，玩杂耍无助于解决问题，因为每接住一发被抛到空中的炮弹，就会使桥承受一股力，这样就会超过桥的承重极限。若是这位使者真的用这法子过桥，他最后就会掉落到山峡之底。

尽管杂耍对于本例并不实用，但它的用途的确不止业余消遣和娱乐。它既复杂得具有一些有趣的特性，又简单得可以为这些特性构建模型。因此，它能为人们提供一种研究其它一些更为复杂的领域的条件。以下三个领域尤其受益于杂耍研究。

一是对体运动与肢体协调的研究。二是机器人学和杂耍机的设计制作，它为实时机械控制原理的研究和应用提供了良好的试验基础。三是数学领域，杂耍模式有着意想不到的数学特性。

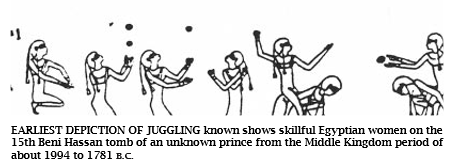
杂耍是一门古老的传统艺术，目前已知的对杂耍的最早描绘是在埃及贝尼哈桑的第15座坟墓中发现的，该墓是公元前约1994年至公元前1781年古埃及中部王国（the Middle Kingdom)时期一位不知名的王侯的。尽管对杂耍早有描绘，但据我们所知，对杂耍的初次科学研究却是在1903年才出现的。当时，埃德加·詹姆斯·斯威夫特在《美国心理学杂志》上发表了一篇文章，文中证明了一些学生学会用一只手抛接两只球的速率。到40年代，早期计算机曾被用于计算被抛物体的轨道，并且还成立了国际杂耍师协会。50年代和 60年代期间，曾有一些人分别进行杂耍的应用研究，其中多数人是在继续 斯威夫特的研究工作，他们用杂耍来比较学习感觉运动技能的普通方法。

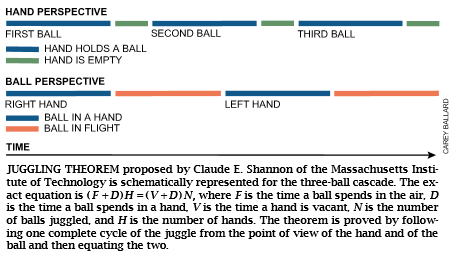
最后，在70年代，人们开始研究杂耍本身的价值，这在麻省理工学院的研究活动中已有所证明。在该院，克劳德·E·香农研制出杂耍机，并系统阐述了杂耍的原理，该理论显示了球的位置与手的动作之间的关系。多路存取计算项目（即Project MAC，后来成了麻省理工学院的人工智能实验室）的西摩·A·佩珀特(Seymour A.Papert)和其他一些研究人员研究了人们掌握杂耍技艺的过程，并且麻省理工学院还成立了杂耍俱乐部，这是最早从事业余杂耍活动并存在至今的专门组织之一。80年代期间，出现了关于杂耍的数学。当时，几位研究人员提出了一种特别的记号，以总结杂耍的模式[参见框图内文字]。

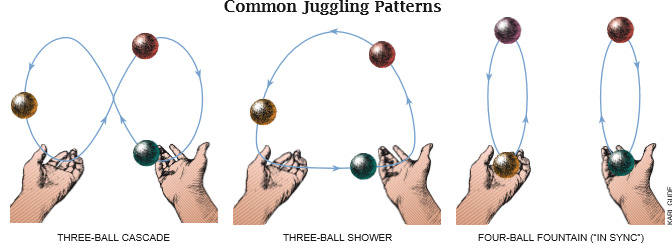
大多数杂耍新手都以模线串接模式（the shower pattern)耍 3只球(绕成一个圆形），尽管以8字对抛模式(the cascade pattern)玩杂耍要容易得多。以8字对抛模式玩杂耍时，两只手交替向另一只手抛球，球的轨线构成一个横着的8字。学会抛接3只球时常只需要几小时或者几天功夫。而随着玩杂耍者抛球接球能力的精熟提高，学会抛接4 只球则可能要花数周乃至数月时间，5只球则要花数月乃至数年。

抛接杂耍物体（以每个物体至少抛接一次即完成一个回合计算）的世界最高记录分别是12个环、11只球或8根棒。杂耍物体的类型之所以对抛接的物体总数有影响，是因为它们在方向正确性、抓握与抛掷难度以及避免碰撞这类失误的余地大小上均有所不同。

学习曲线的极限

人的身体协调能力上的明显限制影响着杂耍技能的掌握并使杂耍物体的数量保持在一定的限度内，这种限制产生于重力，或者更准确地说，产生于牛顿力学。杂耍者要想有足够的时间应付其它的球，每只球就都必须抛得足够高。一只球沿轨线飞行时所花的时间和球被抛扔的高度的平方根是成正比的。随着杂耍物体数量的增加，抛扔的速度和高度都必须迅速增加。

此外，由于人的技能的不完善,还会导致时间和空间两方面的失误。如果抛球过低，就难以避免球与球相互碰撞，因而需要抛球和接球都很迅速，然而这样就容易出现失误。若是抛球较高，就会有较多的时间避免和纠正失误，但这样一来也会使失误更严重，在球抛得只有几米高的情况下，球若抛偏了2度到3度，球的落点就会偏离正确位置30厘米或更多。

香农的理论精巧地概括了杂耍上的时间限制，并且确定了杂耍者手空着或握有球的时间以及每只球在空中飞行时所花的时间之间必然存在的关系。换句话说，若是增加所抛接的球的数量，就会使改变杂耍的速度的余地更小。若是杂耍者把许多只球耍到一定高度，那么，按照该理论，即使只在抛球速度上出极小的偏差，也会使整个杂耍模式毁于一瞬。

杂耍者如何协调肢体，使之在上述限制范围内按同一频率有节奏地运动，这已成为人体运动研究的一个主要焦点。研究人员从耦合振荡子的数学理论中借用了有关概念[参见本刊1994年4期 Steven H.Strogatz和Ian Stewart所撰“耦合振荡子与生物同步”一文]。

耦合振荡的一个基本现象是同步，即两条手臂趋于以相同频率运动。玩杂耍的双手所表现出的特殊类型的协调，取决于杂耍的模式。例如，就8字对抛式杂耍多达扱限的9个球，杂耍者就很难找到机会进行修正和适应，更不用说玩特技和鬼把戏了。

眼睛决不能盯着球

然而，像这样构建的杂耍运动模式的模型却几乎没有提供必要的手眼协调方面的知识。杂耍者必须获得关于手和球的运动这方面的知识。在大多数情况下，“让你的眼睛盯着球”这一指教多少都有些意义，而在杂耍上，这样的指教就意义甚微了。在杂耍过程中，杂耍者的注意力必须从一只球转移到下一只球，这样，杂耍者所看到的，就只是每只球的飞行轨迹的一部分了。

球的飞行轨迹的哪一部分能供给最多的信息且又是视线所注意到的？杂耍学习上常见的指教是“注意最高点”和“在前一只球到达顶点时再抛出下一只球。”1974年，霍德华·A.奥斯汀还在麻省理工学院读研究生时，就曾探查过，技术水平中等的杂耍者要玩好杂耍，必须看到轨线顶点的多大一片区域。他在杂耍者的双手和双眼之间，安放了一块扇形隔板，板上挖有一个楔形缺口。球的飞行轨迹的顶点部分只要可以看到1英寸长那么短一段，这只球就可以成功地接住。这么短的一段距离大致相当于50毫秒的观看时间，这就意味着要玩好杂耍，杂耍者只要不时瞥一瞥球的飞行轨迹顶点部分就行了。

1994年，阿姆斯特丹的弗里大学的托尼·A.M. 范桑特沃德(TonyA.M.van Santvoord)更为详细地研究了手的动作与球的观看之间的关系。他让中等水平的杂耍者戴着液晶眼镜耍三球8字对抛式，这种眼镜按预定的时间间隔开关，因此杂耍者只能时断时续地看到球。根据球在空中的运动和液晶眼镜决定的节奏之间的关系，杂耍者可以推断出三点，一是液晶眼镜开着时的球的位 置，二是可以选择观看球的哪一段飞行轨迹，三是手的动作与视觉信息获取之间的协调程度。

在某些情况下，受试者调整了杂耍动作，使之与液晶眼镜的开关频率相协调。于是，杂耍者就能在球到达飞行轨迹顶点之后立即看见它。实验结果还表明，经过训练之后，杂耍时看见球的重要性便降低了。总的说来，杂耍新手和中等水平的杂耍者耍球时对视觉依赖极大。而杂耍老手耍球时则更多依赖于对球的触觉。事实上，威廉·詹姆斯就曾在其问世于1890年的著作《心理学原理》(The Principles of Psychology)中说，杂耍名家让尤金·罗伯特豪丁（Jean-Eugene Robert-Houdin)能够一边看书一边耍四只球。许多杂耍熟手都能在蒙住眼睛的情况下，连续耍球数分钟之久。

一种似乎合理的假说认为，在学习杂耍的过程中，观看运动中的球能够逐步使触觉变得敏锐准确。杂耍老手能够立刻察觉所要求的抛球角度上的细小偏差，还能立即发觉抛球力量上的小小失误，而杂耍新手却必须看到失误对飞行轨迹的影响。因此，杂耍老手的动作纠正时常对杂耍模式的完善几乎没有干扰。相反，杂耍新手的动作调整时常破坏了杂耍的整体稳定性。

杂耍机器人

由于对人类的杂耍有了深刻认识，使得一些研究人员试图利用机器人来玩杂耍。这类机器人想必会为更为精致、更为完善的自动机打下基础。事实上，杂耍和人们平常的生活内容有许多相同之处，如驾车驶过交通繁忙的大街，在风大的日子去接一只飞球，在拥挤的房间中穿行。所有这些活动都要求人们预料到将要发生的事情，以便组织当前的行动。

香农首创了杂耍机器人学，并于70年代在一台大吊车组件的基础上制作出一台弹球杂耍机。在这台杂耍机上，一些小钢球被从绷得很紧的鼓上弹起，球每在鼓上敲击一下，便“咚”地发出一声令人满意的空响声。弹球杂耍完成起来要比抛球杂耍来得容易,因为弹球杂耍的球是在飞行轨线的顶部即球运动得最为缓慢之时被抓住的。

在香农的杂耍机中，机械臂是彼此相对而固定的。杂耍机构按一种简单的来回摇摆的运动方式动作。每条机械臂向下摆动时便完成一次接球动作，而向上摆动时则完成一次抛球动作。抛球的失误是以短的开槽的导轨代替人的双手来纠正的。球在飞行轨线的顶点附近被抓住，然后便降落在导轨中；机械臂的向下摆动使球滚到导轨的背面,由此使球获得足够的能量而被抛出。香农最初设计制作的原型机能耍三只球，而佐治亚理工学 院的克里斯托弗· G.阿特基森和斯蒂芬·K.沙尔（Stefan K.Schaal)此后按照同样的方式制成的一台杂耍机则能耍五只球。

尽管弹球杂耍机器人已灵巧到家了，但既能耍三球8字对抛式，又能自动纠正失误的机器人却还有待于研制。不过，在这方面已经取得了一些进展。人们已经制作出一些能接球、击球和把球打到空中的机器人。此外，工程技术专家还造出了能在二维范围内玩杂耍的机器人。80年代期间，国际商用机器公司托马斯·J.沃森研究屮心的马克·D.唐纳在一个类似于空中曲棍球（air-hockey)球桌的倾斜、光滑的平面上装上了两个抛球机构，它们能在平面较低一侧边缘的导轨上运动。

1989年，耶鲁大学的马丁·比勒 (Martin BÜhler)和现在密执安大学供职的丹尼尔·E.科迪茨切克把杂耍机器人研制工作又向前推进了一步。他们所采用的不是在导轨上运行的抛球机构，而是一个旋转的棒杆，上面装了一块台球桌的橡皮边，用来把平面上的球往上打。为了控制好球棒以获得同期性的杂耍效果，两位研究人员依靠了所谓的“镜象算法”（mirror algorithm)的帮助。

镜象算法这一概念实质上是由两个概念综合而成的。第一个概念是将球的连续的轨迹转换（即“反映”）成一条联机参考轨迹，以便（通过—个仔细选出的非线性函数）控制机器人的运动。这种镜象算法的优点在于，它使人们没有必要获取在撞击点的球的状态的完整信息，这样的信息在实际情况下是很难获取 的。第二个概念是耍稳定球的垂直运动，它分析出球的能量，看其是否和一次完善的抛投下的理想的能量符合。这样，镜象算法程序便记录下球的位置，计算出球的参考镜象轨迹，以及球的实际的和所要求的能量，并求出须在何时，须以多大力量击球。利用这种镜象算法的扩充版本，该机器还能表演一种二维、双 球，单手杂耍。它能交替地用在枢轴上转动的球棒的左边部分和右边部分把球径直击向上，使球的轨迹形成两个独立的行列。

观看这种镜象算法如何操纵机器人玩杂耍是很怪异有趣的。若是你扰乱一只球的运动，机器人手臂就会做出一些急促的动作，这些动作看起来虽然从杂耍演员的角度看来完全不自然，却又能令人不可思议地迅速恢复为平稳的杂耍动作。这种镜象算法虽然能够灵巧地控制击球动作，但它还不足以解决接球动作可控的杂耍这一更为困难的问题。

除了弹球和击球以外，机器人还能进行许多其它的与杂耍有关的活动，其中包括来回拍打棍棒，用一只漏斗形的手使球跳起来、保持平衡、向上抛球、接球以及打一种改进的乒乓球。尽管取得了这些进展，但至今还没有一台机器人能短暂地象人一样玩杂耍。然而，杂耍的科学研究毕竟是一个相对来说比较新的研究领域，而在过去20年里，这方面的研究的进展确实很显著。也许要不了多久我们就会这样问道：“机器人是怎样手中握着三只炮弹通过这吱嘎作响摇摇欲坠的桥的呢?”