互动科普

“海格服装公司（Haggar）的物理学家开发出了‘量子休闲裤’”——这是以讽刺见长的美国《洋葱报》（Onion）上一篇文章的大字标题。文章解释说，这些非牛顿性的裤子充分利用了“薛定谔裤”奇异的双重性，可以匪夷所思地同时当成正装西裤和休闲裤来穿。很显然，《洋葱报》的作者们是在讽刺10年来充斥于科普媒体上的，有关量子计算的沉闷文章。

许多文章都会犯同一个常见错误，比如2007年2月15日《经济学人》（Economist）上刊登的一篇文章就声称，量子计算机原则上能够快速求解一类特别困难的数学难题。这类难题被称为“NP完全问题”（NP-complete problems，具体解释请见第80页图释），就算是目前性能最好的计算机也无法快速求解（这一现状好像尽人皆知）。他们之所以推测量子计算机能够完成这样的壮举，并不是因为它们能像“量子休闲裤”那样，同时当成西裤和休闲裤来穿，而是因为量子计算机的硬件能够同时处理每一种可能出现的答案。

如果我们真的建造出万能计算机，能在瞬间求解NP完全问题，整个世界就会大不一样：我们可以让万能计算机寻找股票市场、天气状况或大脑活动记录中可能存在的变化模式。这种计算机不同于今天的计算机，寻找这些变化模式将完全成为常规运算，不需要对问题本身有任何深入的了解。这种万能计算机还可以自动检验数学上的创造性想法。对于任何一个数学圣杯，比如一个多世纪以来都得不到证明的哥德巴赫猜想（我国数学家陈景润在20世纪60年代，曾经证明了哥德巴赫猜想的1+2问题，距离最终证明1+1仅一步之遥，但50年来这一难题依然无人能解）或黎曼猜想，我们只要指定一个有限数字，比方说10亿，让神奇计算机搜索这么多个字符的所有可能组合，从中寻找这些猜想的肯定或否定性证明。（如果一个证明远远超过10亿个字符的话，也许我们就不会有兴趣去看了。）

如果量子计算机真能带来上帝般神奇的数学能力，或许我们就得等到曲相推进发生器（warp-drive generator，目前仍是幻想的超光速发动机）和反重力盾上市的时候，才能在货架上看到它们的踪影了。不过，尽管我们不应该接受通常那种夸大其词的说法，在我看来，把量子计算等同于科学幻想而置之不理同样是一种误导。相反，我们应该去了解量子计算机的局限性，弄清我们真的拥有量子计算机后，它们到底能做些什么。

量子计算的概念，是在26年前，由物理学家理查德·费曼（Richard Feynman）最早提出的。自那以后，在寻找量子计算机擅长解决哪些问题方面，计算机科学家已经取得了很大的进展。按照我们目前的理解，量子计算机能够极大地加快若干特定问题的求解过程，比如破解互联网上商业交易中广泛采用的加密编码。不过也有证据强有力地表明，对于下国际象棋、调度航班和证明定理等其他问题，量子计算机会和今天的传统计算机一样，面临许多同样的算法局限。这些局限与建造量子计算机时将会遇到的实际困难［比如退相干（decoherence），即量子计算机与周边环境之间发生的、能够引起差错的有害相互作用］完全是两码事。具体而言，即使物理学家设法建造出了没有退相干效应的量子计算机，它通过编程能够完成的事情仍然会受到数学方面的限制。

难上加难

对于破解密码之类的一些问题，量子计算机能够提高运算速度，对于其他问题却不能，这是怎么回事？更快的计算机不就是运算速度更快吗？答案并没有这么简单，要想解释其中的原因，我们要直接触及计算机科学的知识核心。对计算机科学家来说，一个问题的关键因素在于，随着该问题规模的扩大，求解所需的时间如何增长。这种时间是用某一种算法求得一个解所需的基本步骤的数目来衡量的。比如，利用小学算术的方法，我们乘两个n位数所需的总时间，大概随位数的平方——n2而增长（这样的时间量被称为“多项式时间”）。但是，要把一个n位数分解质因子，即使用目前已知最先进的算法，所需的时间也会随位数的指数（确切地说，是2的  次方）增长。因此，因子分解实质上要比乘法难得多——如果要对上千位的数字进行运算，因子分解和乘法之间的差别，要比Commodore 64（20世纪80年代初出产的最早的一种家用计算机）和超级计算机之间的差别重要得多。

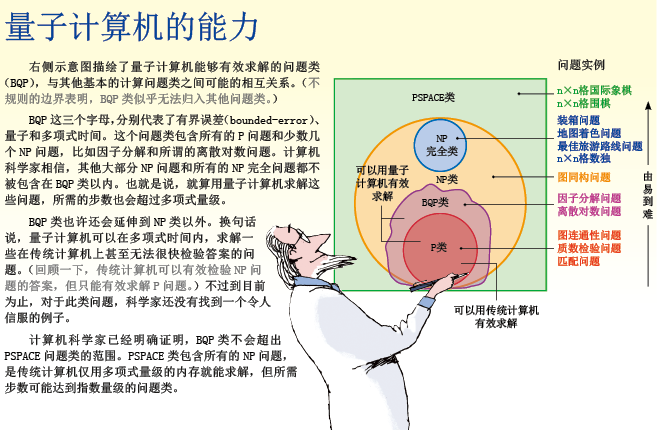
有些问题，我们已经找到了一种算法，可以在有限步数内求解，步数随n的某一固定幂次（比如n、n2或n2.5）增长。这样的问题即使n值很大，计算机也能在合理的时间内求解。计算机科学家把这样的算法称为有效算法（efficient algorithm），把可以通过有效算法求解的问题归类为复杂类P（complexity class P），其中P代表多项式时间。

给定一张地图，是否每个城市都与其他任何一个城市直接相连？这个问题就是复杂类P中的一个简单例子。P类中还包含一些有效解法不这么一目了然的问题，比如：给定一个整数，它是13这样的质数（prime）还是12这样的合数（composite）？给定一份希望结婚的女士和男士的名单，可不可能每个人都找到如意的配偶？

不过有些看似平常的问题，却无法归入P类。比如说：给你一堆大小不同的盒子，每个盒子的尺寸都已知，让你找出把这些盒子放进汽车后备箱的方法；给你一张地图，让你把每个国家都涂上红、绿、蓝三色中的一种，要求任意两个相邻国家的颜色都不同；给你一张“千岛之国”的地图，岛与岛之间通过桥梁相连，让你找到一条最佳旅游路线，每个岛都逛到，而且只逛一遍。最笨的办法当然是每种可能性都尝试一下，不过这种办法需要太多时间。尽管已经找到了一些不那么“笨”的算法，但没有一种可以从根本上改善求解速度。每种已知算法所需的时间，都随问题规模的指数而增多。

从数学上可以证明，我刚才列出的三个问题拥有非常有趣的性质：它们都是“同样”的问题。我的意思是说，如果其中任何一个问题能够找到有效算法，那么另外两个问题就能迎刃而解。这个令人瞩目的结论是由加拿大多伦多大学的斯蒂芬·A·库克（Stephen A. Cook）、美国加利福尼亚大学伯克利分校的理查德·卡普（Richard Karp）和美国波士顿大学的利奥尼德·莱文（Leonid Levin）在20世纪70年代得出的，当时他们发展出了NP完全理论（NP-completeness）。

NP代表“非确定性多项式时间”（nondeterministic polynomial time），就算不知道这是什么意思也不必担心。简单来说，NP指的是这样一类问题：一旦找到一个解，就可以在多项式时间（比如n2个步骤）内判断它是否正确——哪怕这个解本身很难找到。比如，如果给你一张绘制了上千个岛和桥的地图，要想找出每个岛都逛到而且只逛一遍的最佳路线，也许要花好几年的时间。不过，如果有人给你提供了一条路线，检查它是不是我们想要的最佳路线就十分容易。如果一个问题具有这样的性质，我们就说它属于NP类。许多重要的实际问题都属于NP类。需要指出的是，所有的P问题同时也都是NP问题，换句话说，P类被包含在NP类中。如果能够快速求解一个问题，迅速检验解的正确性当然就不在话下了。

NP完全问题实际上是最困难的NP问题。这些问题拥有库克、卡普和莱文发现的那种性质：只要其中任何一个问题能够找到有效算法，该算法就可以用来求解其他所有的NP问题。

如果NP完全问题存在有效算法，那就表示计算机科学家目前对P、NP和NP完全问题的分类是完全错误的，因为这将意味着每一个NP问题（包括所有的NP完全问题）事实上全都是P问题。换句话说，P类将等于NP类，用数学式来表达就是P = NP。

这样的算法存在吗？P真的等于NP吗？这可是个价值百万美元的问题——美国马萨诸塞州剑桥市的克雷数学研究所悬赏100万美元征求这个问题的答案。这个问题至少已经在美国的三部电视剧集［《辛普森一家》（The Simpsons）、《飞出个未来》（Futurama）和《数字追凶》（NUMB3RS）］中客串出场。

在人们提出这个问题以来的半个世纪里，没有人找到过任何一个NP完全问题的有效算法。因此，今天的计算机科学家几乎一致认为，P不等于NP，或者说P ≠ NP，尽管我们还没有聪明到能够明白其中的道理，或者把它像定理那样证明出来。

量子的本领

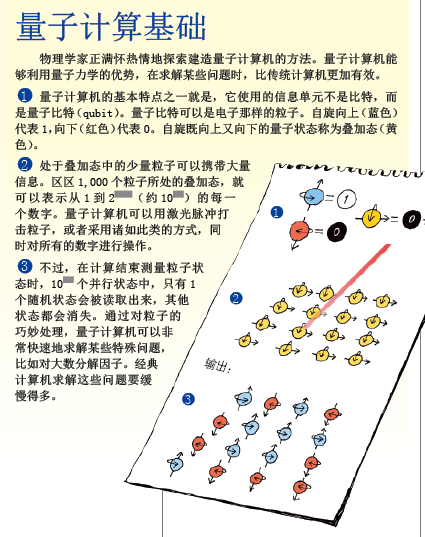
如果我们承认P ≠ NP，那么在多项式时间内求解NP完全问题就只剩下唯一一个希望：那就是扩展我们所称的“计算机”的概念。乍看起来，量子力学似乎恰好给我们提供了所需的那类资源。量子力学让我们有可能在数量相对较小的粒子状态中存储和操作大量信息。为了说明这一点，我们可以想象有1,000个粒子，对其中任何一个粒子的自旋进行测量时，所得的结果不是向上就是向下。对我们来说，一个粒子自旋向上或向下意味着什么其实无关紧要，重要的是这个粒子拥有某个性质，在我们测量时体现出非此即彼的两种状态之中的一种。

为了描述这样一组粒子的量子状态，我们必须对测量这些粒子时可能出现的每一种结果指定一个数字。这些数字被称为可能输出结果的幅值（amplitude），与每一种输出结果出现的可能性有关。不过幅值又不同于概率，量子幅值可正可负（实际上，它们是复数）。比如，描述所有1,000个粒子的自旋全都向上的可能性需要一个幅值，而描述前500个粒子自旋向上、后500个自旋向下的可能性又需要另外一个幅值，以此类推。1,000个粒子共有21,000种可能的输出结果，也就是大约10300种，因而也就需要这么多数字来加以描述——这些数字的数目甚至超过了可见宇宙中的总原子数！这种情况用术语来描述，就是1,000个粒子处于那10300种状态的叠加态（superposition）中。

换句话说，我们能够在1,000个粒子中，同时存储10300个数字。于是，对这些粒子和一些辅助粒子进行各种操作，比如用一系列激光脉冲或无线电波来轰击它们，我们就能实现一种算法，同时对10300个数字（每个数都是一个可能的解）进行变换。如果到了操作的最后阶段，我们能够把粒子的最终量子态精确读取出来，我们就能拥有一台万能计算机：它有能力同时检验10300个可能的解，最终让我们迅速分辨出正确的那个解。

可惜的是，这种说法有一个容易被忽视的漏洞。当这些粒子被测量时（这是读取最终状态必不可少的一步），量子力学法则限定，测量会从10300个可能结果中随机选出一个，其他结果全都会消失不见。（现在回过头去重新思考本文开头海格服装公司研制的量子休闲裤，只要你试穿这种裤子，会发现自己要么穿着正装西裤，要么穿着休闲裤，不可能两样都是。）看来，这种量子算法并不比使用经典计算机随机选取可能的解，再加以检验的“笨办法”好多少——不论采用哪种方法，最终我们还是只能知道一个可能的解是否正确。

令人高兴的是，我们能利用一些技巧来发挥量子粒子的优势。如果正负幅值组合在一起，它们就会相互抵消，这种现象被称为破坏性相干（destructive interference）。因此，一种优秀的量子计算机算法应该确保通向错误答案的计算路径以这种方式彼此抵消。它还应该确保通向正确答案的路径都具有符号相同的幅值，这样就会发生建设性相干（constructive interference），从而提高最终测量这些粒子时得到正确答案的可能性。

哪些计算问题可以让我们设计出这样的相干，让求解该问题的量子算法的步骤比经典算法更少呢？

1994年，彼得·肖尔（Peter Shor，目前在麻省理工学院）发现了第一例能够大大加快实际问题求解速度的量子算法。确切地说，肖尔证明量子计算机能够在多项式时间，也就是按n2增长的步数内，对一个n位数分解因子。如果使用经典计算机，正如前面已经提到的，已知最好的算法所需的步数也会以指数增长。

黑箱运算

因此，至少对于质因子分解，人们使用量子方法确实可以大大提高问题的求解速度，把指数时间缩短为多项式时间，实现所谓的“指数加速”。但是，质因子分解既不属于已知的NP完全问题，也没有任何专家认为它会是个NP完全问题——这与广泛存在的误解恰恰相反。为了创造这种量子算法，肖尔利用了合数及其因子的某些特殊数学性质。这些性质特别适合产生让量子计算机能够发挥优势的建设性和破坏性相干。但是，NP完全问题似乎并不具备这些特殊性质。到目前为止，研究人员只找到了少数几例量子算法，似乎确实能够有效地将某个问题的求解步数从指数量级减少到多项式量级。

因此，到底存不存在有效求解NP完全问题的量子算法，这个问题依然没有得到解答。人们做了大量尝试，仍然没能找到这样的算法。不过，计算机科学家也没能证明这样的算法不存在——这一点并不奇怪，毕竟我们连“NP完全问题不存在能在多项式时间内求解的经典算法”这个命题都无法证明。

我们只能说，一种能够有效求解NP完全问题的量子算法，必须像肖尔算法那样利用问题本身的结构，只不过利用的方式远远超越了当今的技术水平。把问题当作一个没有结构的“黑箱”，让量子计算机并行检验指数多个解的办法，是无法实现指数加速的。不过，黑箱方法确实可以或多或少地挖掘一定的加速潜力，计算机科学家已经能够确定，这种加速能做到多好，又会受到怎样的限制。产生这种加速的算法，是量子计算机算法中的第二大类。

我们可以举个例子来说明什么是黑箱方法。假设你在寻求一个困难问题的答案，而你能做的唯一操作，就是猜测一个解，看它是否行得通。比方说，这个问题共有S个可能的解，其中S随问题规模n的增加而呈指数增长。也许你够幸运，第一次就猜对了答案；也可能很倒霉，尝试了S次才成功通过。平均来说，你需要尝试S/2次。

现在，假设你可以在量子叠加态中检验所有可能的解。1996年，美国贝尔实验室的洛夫·格罗弗（Lov Grover）开发出一种算法，仅用大约  步就能找到正确的解。对一些问题来说，从S/2加速到  是很有用的——如果可能的解一共有100万个，那么你需要尝试的次数就会从50万下降到1,000次。但是，平方根并没有把指数时间转变成多项式时间，只过不它的指数较小而已。而且，格罗弗的算法已经达到了此类黑箱搜索的极限：1994年，研究人员已经证明，任何量子黑箱算法都至少需要  步，才能找到答案。

过去十年来，研究人员已经证明，除了上面这个例子以外，其他许多问题都存在着类似的加速极限，包括在选举中统计选票、在地图上寻找最短路线、玩策略类游戏（比如下国际象棋或围棋）等。所谓的“碰撞问题”（collision problem）是目前特别困难的一个典型问题，就是要在一份长长的列表中找出两个一模一样的项。如果能够找到快速求解这个问题的量子算法，电子商务安全的许多基石就会在量子计算机的世界中变得不堪一击。

在列表中寻找指定的一项，就像在干草堆中寻找一根银针；查找两个相同的项，则相当于在干草堆中找出两根完全相同的干草——这给碰撞问题提供了一种量子计算机有可能利用的结构。不过，我在2002年已经证明，在这种黑箱模型中，用任何量子算法来求解碰撞问题都必须花费指数时间。

不可否认，这些黑箱极限并没有排除以下这种可能性：NP完全问题，甚至更困难的问题，也许存在有效量子算法尚待人们去发现。不过，就算这样的算法真的存在，它们也必须以某种我们今天未曾见过的方式，利用问题本身的结构——就像求解问题的有效传统算法必须针对问题设计出某种运算技巧一样。量子魔术本身并不能担此大任。基于这种观点，许多计算机科学家现在不仅猜测P ≠ NP，还推测量子计算机不可能在多项式时间内求解NP完全问题。

奇异的理论

量子计算机很可能触及到了计算能力的极限——也就是说，量子计算机是符合物理学定理的最通用的计算机。我们所知的一切都支持这种说法。不过，物理学家还没有归纳出一套物理学的终极理论，因此谁也不能保证：有一天不会出现某种未来理论，能够提供有效求解NP完全问题的物理方法。也许你已经预料到了，人们正在假想更加强大的计算机，其中一些将使量子计算机看起来落后得如同自动售货机。不过，那些超凡的计算机全都是以物理学定律可能出现的改变为前提的。

量子力学的核心特点之一，是一条被称为线性（linearity）的数学性质。1998年，当时同在麻省理工学院的丹尼尔·S·艾布拉姆斯（Daniel S. Abrams）和塞思·劳埃德（Seth Lloyd）证明，如果能在量子力学方程中引入一个小的非线性项，量子计算机就可以有效求解NP完全问题。不过先别高兴得太早，如果这样的非线性项确实存在，我们就会违反海森堡不确定性原理，还能超光速发送信号。正如艾布拉姆斯和劳埃德指出的，这一结果的最大意义也许就在于，它有助于说明为什么量子力学是线性的。

另一种假想的计算机，可以把无穷多步挤压到一段有限的时间内，从而实现超强计算能力。遗憾的是，按照物理学家当前的理解，时间在10-43秒（普朗克时间）的尺度上，似乎会被淹没在量子涨落的海洋里，变成一种类似泡沫的东西，而不再是一条均匀光滑的直线。因此，这类计算机看起来不可能实现。

如果时间无法任意细分，也许有效求解NP完全问题的另一条途径就是利用时间旅行。研究这一问题的物理学家谈论的并不是时间机器，而是所谓的“闭合类时曲线”（closed time-like curve，缩写为CTC）。CTC本质上是物质或能量在空间和时间中所经的一条路径，沿着它，物质或能量就会追上它的过去，形成一个闭环。现有的物理学理论对CTC是否存在还得不出定论，但这并不妨碍我们去研究这样一个问题：如果CTC存在，它会对计算机科学带来什么影响？

利用CTC实现计算加速的方法似乎显而易见：给计算机编写一个求解某一问题的程序，不管求解过程需要多久，只要赶在计算机启动之前把答案送回来就行了。不过，这个简单的想法并不可行，因为它忽略了著名的“祖父悖论”（grandfather paradox）。祖父悖论很简单：你回到过去杀死了自己的祖父（不过那样的话，你就不会出生，因此就不可能回到过去，于是你的祖父就不会被杀，会顺利地生儿育女，然后你就会出生，回到过去杀死自己的祖父……）在我们设想的这个例子中，如果你收到了发自未来的答案后，顺手关掉了计算机，情况又会如何？

1991年，英国牛津大学的物理学家戴维·多伊奇（David Deutsch）详细阐述了一种CTC计算模型，能够避免出现上述自相矛盾的困境。在多伊奇的模型里，大自然会保证事件沿着组成CTC的循环时间线展开，这样就不会发生悖论。利用这一事实，我们可以编程让计算机在CTC内反复循环，从而求解困难问题。

确实，利用CTC，我们不仅可以有效求解NP问题，甚至还能求解看起来规模更大的一类问题——PSPACE问题。PSPACE指的是可以在传统计算机上用多项式量级的内存，但可能要用指数时间来求解的一类问题。实际上，CTC可以把时间和空间当作能够互换的计算机资源。（我直到现在才提到多项式内存的原因在于，如果计算机能够访问的内存数量超过多项式量级，对于P和NP问题来说，内存的约束就毫无分别。）最近，我和加拿大安大略省滑铁卢大学（University of Waterloo）的约翰·沃特罗斯（John Watrous）合作证明，在CTC中用量子计算机替代传统计算机，并不能有效求解超出PSPACE类以外的任何问题。换句话说，如果CTC真的存在，量子计算机就不会比传统计算机更加强大。

计算上的局限

物理学家们还不知道，未来的理论会不会允许任何一种万能计算机的存在。不过不必否认我们的这种无知，我们甚至可以从另一个角度来审视这种无知。我们可以先假设NP完全问题就是难以求解的，然后再来研究这一假设对物理学产生的影响，而不是从物理学理论出发，考察这些理论在计算方面的应用。比如说，如果CTC能够让我们有效求解NP完全问题，那么从NP完全问题不可能有效求解的假设出发，我们就会得出CTC不可能存在的结论。

对有些人来说，“NP完全问题不可能有效求解”的假设似乎太过武断。不过对我来讲，这和热力学第二定律或超光速通讯不可能实现的假设没有区别。那两条最初也是技术上的极限，随着时间的推移，已经取得了物理学定律的资格。没错，说不定热力学第二定律明天就会被实验推翻——不过这样的事情至今仍未发生。物理学家们发现，假设第二定律的正确性非常有用，他们还用这一假设研究了从汽车发动机到黑洞的所有问题。我预言，“NP完全问题难以求解”的假设总有一天会被人同样看待，被视为描述我们宇宙本质属性的一条基本原理。现在还无法预言，这样的基本原理未来会带来怎样的理论突破和实际应用。

与此同时，我们也要知道，不要期望量子计算机会产生奇迹。量子计算机似乎也有局限，这一想法或许会让一些人感到失望。不过，我们可以更加乐观地看待这些局限性。这些局限性意味着，就算某些加密编码在量子计算的世界里能够被破解，还会有其他一些编码可能是安全的。它们还增加了我们对于量子计算机最终有可能实现的信心——因为一项新技术听起来越像科幻小说，我们就越会怀疑。（假设两位推销员向你推销产品，一位卖的是可以从量子真空中产生无限免费能量的装置，另一位卖的则是比去年的型号能效更高的冰箱，你会更相信谁呢？）最后一点，这样的局限性能够确保计算机科学家不至于无事可做，他们还必须继续设计新的量子算法。没有任何限制的计算机，就像没有后脚跟的阿喀琉斯或没有氪石（kryptonite）的超人一样（阿喀琉斯的后脚跟和超人的氪石都是他们的致命弱点），很快就会让人感到乏味。