互动科普

月球为何不会掉落下来？

脱离枝头的苹果会掉落到地面，那么，月球为什么却不会掉落下来呢？这个长期困惑古人的难题最后是由英国的一位天才科学家艾萨克·牛顿（1642〜1727）解决的。

按照牛顿在1687年发表的“万有引力定律”，无论苹果、月球还是地球，事实上所有物体，彼此之间都施加有一种相互吸引的作用力。因此，与苹果和地球之间相互吸引一样，月球和地球之间也在相互吸引。

既然如此，那么为什么月球经过了如此长的时间也没掉下来与地球相撞？投出一只苹果，它不久就会掉落到地面。用力以更大的速度投出去，它会飞过更远的距离才掉落到地面。如果不断增加投出的速度，苹果飞过的距离便会不断增加，最后，苹果就有可能不掉落到地面，而是围绕地球飞行一周。

围绕地球飞行一周的苹果其实已经不会掉落到地面，而是持续地围绕地球运动。月球以每小时3600公里的巨大速度围绕着地球运动，所以它永远也不会掉落到地面。

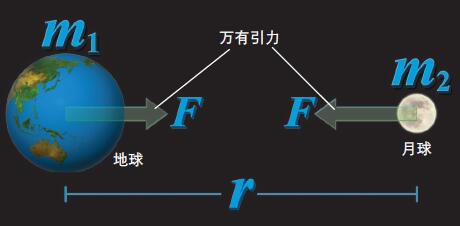
图. 计算万有引力

作用在两个物体之间的万有引力的大小F [牛顿] 可以由它们的质量m₁、m₂ [千克] 和它们之间的距离r [米] 通过计算求得。公式中的G叫做“万有引力常数”，其数值为约6.67×10^-11 [牛顿·米²/千克²]。

以地球和月球之间的万有引力为例。地球的质量为约6.0×10²⁴ [千克]，月球的质量为约7.3×10²² [千克]，地球中心和月球中心之间连线的长度为约3.9×10⁸ [米]。由这3个数值计算得到地球和月球之间的万有引力大小约为2×10²⁰ [牛顿]。万有引力是相互作用的力，地球以这样大的力吸引月球，月球也以这样大的力吸引地球。在地球和苹果的例子中，物体之间的距离大致等于地球的半径，即约6.4×10⁶ [米]。

火箭抛弃自身一部分的推动策略

法国哲学家笛卡尔（1596〜1650）说过一句流传了几个世纪的名言：“我思故我在”。他也是为了查明隐藏在宇宙背后的那些定律而一直在进行思考的一位科学家。

笛卡尔认为，空间充满了大量细小的微粒，它们形成一个个“旋涡”。宇宙中的一切全都是这些旋涡带动的结果。于是，笛卡尔从“动量”着手来考察物体的运动。他相信宇宙是上帝的创造，并认为“按照上帝的意志，宇宙的全部动量的总量始终保持不变”。

笛卡尔的“旋涡”概念后来被人们否定，但是他的“动量”思想却被现代物理学保留了下来。在现代物理学中，动量被定义为“质量m×速度v ”。“物体所具有的总动量在没有外力作用的条件下始终保持不变”，这就是“动量守恒定律”。这条定律已经得到了前两页所介绍的牛顿理论的严格证明。

掌握了这条定律，加以巧妙利用，我们才有可能实现宇宙航行。静止在宇宙空间的火箭的动量为零。动量为零，乍一看，这似乎意味着我们没有办法用火箭推动宇宙飞船向前运动。可是火箭可以通过燃烧燃料向后方喷射气体，这些气体具有“指向后方的动量”，根据动量守恒定律，火箭能够因此而获得向前推动的推力。

在这个例子中，动量守恒是指火箭和它向后喷出的气体两者的总动量始终等于零。因此，火箭向后喷出气体，它就获得了与喷出的气体的动量大小相同、方向相反的指向前方的动量。换句话说，火箭能够通过向后喷射气体来使自身向前运动。

（本文发表于《科学世界》2012年第7期）