互动科普

有关量子“涨落”的不等式

实际上，除海森堡不等式之外还存在着所谓“罗伯特森不等式”（方程形式有别于海森堡不等式），它在形式上与海森堡不等式非常类似，但是意义则完全不同。

在罗伯特森不等式中，用“位置涨落”代替了原来海森堡不等式中“位置误差”，而“动量扰动”也换成了“动量涨落”。误差、扰动也好，涨落也好，都是用来表明“不确定性”的词汇，意义非常相近，一直以来这些词汇经常被混同。罗伯特森不等式是可以用数学来严格证明的。“有了这个证明，海森堡不等式的证明也可以用类似的方式，”小泽教授解释说。

在罗伯特森不等式中出现的“涨落”，也叫“量子涨落”，是量子力学中特有的概念，理解起来稍微有一点困难，下面我们大致介绍一下。

“误差”和“运动扰动”都是用来表明对测量发生之前物体的位置和动量能够了解到何种程度的物理量。而“涨落”则与测量毫无关系。诸如电子这样的微观粒子原本就具有不确定性，在空间中延展，“云一般”弥散于空间中。即使是单个电子，也犹如会分身术一般，可以同时出现在不同的地方。在其弥散的范围之内，测量之前根本无法预言它到底会在哪里出现。

物理学家或者对量子力学有较多了解的人应该会注意到，两个不等式的意义有明显的差别，但是在20世纪80年代中期完备的量子力学测量理论完成之前，没法证明海森堡不等式，理论一直处于一种混乱的局面。

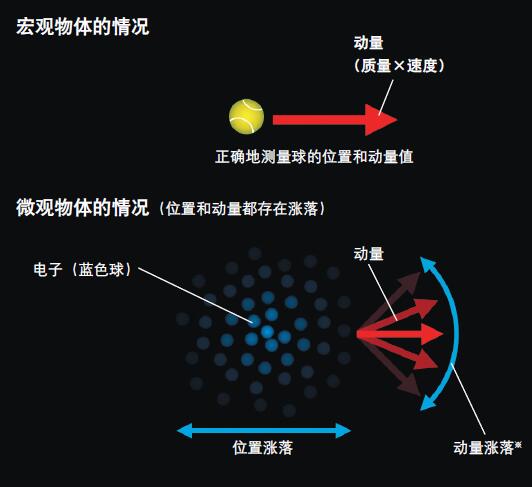
图. 量子涨落

引力波争论引出新的情况

20世纪80年代的“引力波的探测极限问题”使情况发生变化。所谓引力波是空间的弯曲像波一样向外传播的现象。根据爱因斯坦的广义相对论，早在1918年就预言了引力波的存在，但至今还没有直接的观测结果。比如说，在某处两个黑洞量级的“超大质量”天体发生碰撞，将会引起激烈的天体物理现象，引力波也就会跟着产生。因此，将来可能会诞生不用光而用引力波探测天体物理现象的“引力波天文学”。

当引力波到来的时候，空间会发生伸缩。也就是说如果能够精密地测量距离和距离随时间的变化的话，就能知道引力波已经到来。但是这种距离的改变是极其微小的。考虑到我们距发生源的距离和发生源本身的类型，在地球到太阳这样的距离尺度上典型的空间伸缩带来的距离改变也只有一个原子的大小。

实用的引力波探测装置是在“激光干涉仪”上进行的，使用激光来检测镜子与探测装置之间的距离是否发生改变。由于这种实验异常精密，像“光压对镜子的影响”这种一般情况下根本没有必要考虑的问题就变得不可忽略了。如此一来，“采用干涉仪的方法必然存在探测的极限，应该选用其他的探测方法”的呼声高了起来，这引起了是否存在探测极限的讨论。

这个问题是由小泽教授在20世纪80年代中期确立的“量子测量理论”解决的。根据这个理论，人们知道像干涉仪的探测极限之类的问题是可以被“突破”的。从那之后到现在，引力波探测的主流方法一直使用干涉仪。“我认识到要想突破干涉仪的探测极限，必然导致海森堡不等式的不成立，因此我放弃海森堡不等式转而从研究其他的不等式入手。”小泽教授回忆当时的情况时说。

后来小泽教授终于从数学上推导出用以代替海森堡不等式的新的不等式，并于2003年发表。通常也被叫做“小泽不等式”。

形式上，小泽不等式在海森堡不等式的左边加入两个新的有关“涨落”的项。这样，小泽不等式就成了既能包含海森堡不等式的内容，又能适用于所有的实验测量的普遍关系式。

另外，小泽不等式相当于在量子力学的测量上替代了海森堡不等式的地位，并没有否定前面提到的有关量子涨落的“罗伯特森不等式”。罗伯特森不等式的正确性今后也不会改变。今后如要修改量子力学教科书的话，将会是分别讲述小泽不等式与罗伯特森不等式。

（本文发表于《科学世界》2012年第7期）