互动科普

初次检验海森堡不等式

在维也纳科技大学的长谷川钓司副教授及其小组通过实验检验了海森堡不等式和小泽不等式。长谷川副教授说：“这次实验是对海森堡不等式本身的首次检验。”海森堡不等式从1927年提出以来，在长达80多年的时间里一直没有从实验上进行检验。“海森堡不等式中的位置误差和动量扰动的数值非常小，以前根本没有到达如此精度的测量技术，”小泽教授接着说，“因此，说起误差、扰动一直是理论上的事，测量的方法是直到最近才知道的。”无论在理论上还是技术上，这都是困难的课题。

在长谷川和小泽教授使用的实验方法中，不是测量位置和动量，而是测量中子“自旋”的指向。中子是原子核中不带电荷的中性粒子。

中子可以看做是一个小小的磁石。这个小磁石北极所指的方向就是中子自旋的方向，相对磁场强度的量就是自旋的大小。

本次实验中，长谷川副教授及其小组采用的方法是：测量从中子源发射出来的中子，首先测量其在x轴的分量，然后测量与x轴垂直的y轴的分量。

人们知道中子自旋的x轴分量与y轴分量就同位置与动量一样符合不确定性原理。也就是说存在着减小x分量的误差就会增大y分量的扰动这样的关系。

长谷川副教授的小组变换各种条件进行实验，然后把从实验中得到自旋的x分量的测量误差与y分量的测量误差，根据小泽教授的测量理论进行计算。结果确认，所有的实验结果都表明海森堡不等式不成立，而小泽不等式成立。与测量位置和动量不同，测量自旋，特别是中子的自旋能够达到非常高的精度。这才使得不确定性原理的检验成为可能。

小泽不等式推进了量子力学

在受量子力学支配的微观世界的精密控制技术领域，小泽不等式在未来可能有广泛的应用。之前提到的引力波探测和引力波天文学、纳米技术，以及“量子计算机”、“量子加密”等未来革新的信息技术（量子信息技术）中，都预料会有所应用。

量子计算机与现在的计算机有着根本不同的原理，还处于基础研究阶段。至少对因数分解这样的特殊计算要求来说，现行的计算机花费几亿年都解答不出的问题，在量子计算机上可能只花费非常短的时间。

本次小泽不等式被实验验证是正确的，否定了海森堡的不确定性原理，但绝不是推翻了量子力学本身。小泽不等式把量子力学向更加精密的方向推进了一步，打开了进一步应用量子力学造福现代社会的大门。

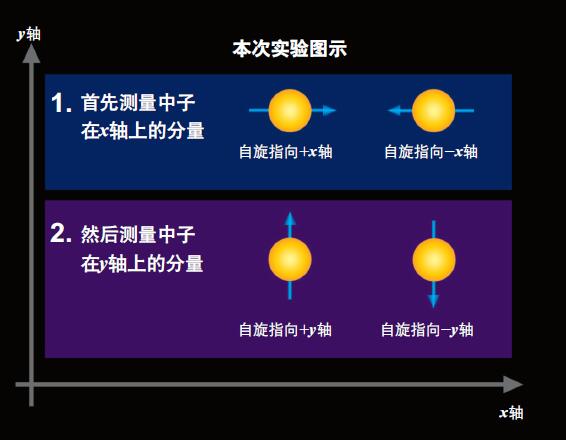
图. 本次中子自旋实验

（本文发表于《科学世界》2012年第7期）