互动科普

随着数字的增大，素数的分布变得越来越稀疏，寻找素数也变得越来越困难。那么，会不会在超过某个界限之后就再也不存在素数了呢？还是说，素数是无穷的，不管数字有多大，还是会零星地跳出几个素数呢？

古希腊数学家欧几里得用一个非常简单的方法回答了这个问题，证明了素数有无限多个。

欧几里得认为：假设素数是有限的，只有“2、3、5”这3个素数。那么，其余的所有自然数都是这3个素数的乘积，都是合数（参照第26页“1是素数吗？”）。也就是说，其他所有自然数都能被2、3或5整除①。这3个素数的乘积再加1为31（2×3×5+1=31），不管用2，还是用3或5都无法整除，余数都为1。这一结果与①相悖，所以“只有3个素数”的假设是错误的。

那么，我们来增加素数的个数，假设只有“2、3、5、7”这4个素数。这4个素数的乘积加1为2×3×5×7+1=211，既不能被2和3整除，也不能被5和7整除。也就是说，在假设的有限个素数之外，还存在着其他素数。

显然，不管怎样增加素数的个数，得到的结论都相同。只要假设素数是有限的，用上述方法（所有素数相乘再加1）就永远可以得到一个这些素数无法整除的素数。因此，“素数的个数是有限的”这一假设不成立。既然如此，素数也就应该有无穷多个。

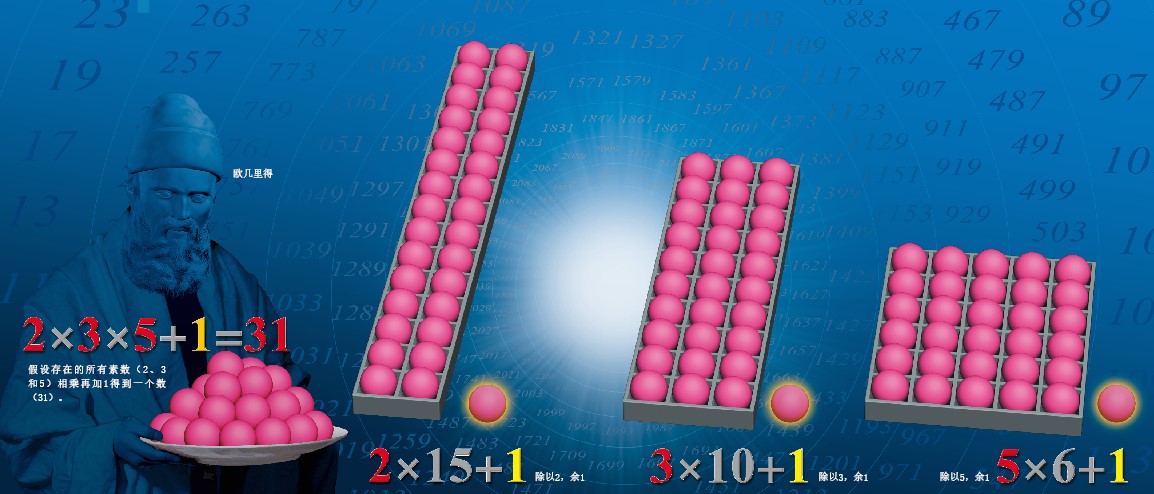证明“素数是无限的”

假设素数的个数是有限的（例如，2、3和5），那么肯定存在一个不能被这些素数整除的数。这就意味着，在假定的有限个素数之外还存在着其他素数。只要假设素数是有限的，用上述方法就永远可以得出有一个素数不在假设的素数集合中的结论。因此，原先的假设不成立。就这样，欧几里得从理论上证明了素数的个数是无穷的。

（本文发表于《科学世界》2013年第6期）