互动科普

千百年来，素数的分布规律一直让数学家感到困惑。神出鬼没的素数到底藏在哪里呢？貌似毫无规律的背后是否有规可循呢？年仅15岁的小高斯目不转睛地盯着素数表，努力探寻着素数的分布规律。

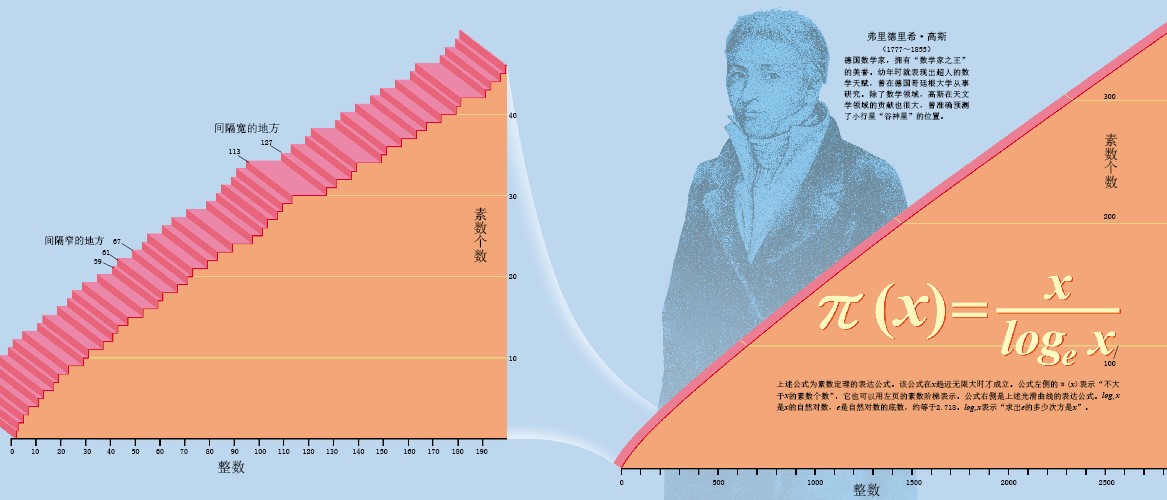
为了更好地理解高斯的想法，先让我们来了解一下什么是“素数阶梯”吧。在整数列中每出现一个素数，阶梯就升高一个台阶，结果就会出现下图所示的阶梯，每级台阶的宽度都不相同。我们把这条由素数构成的阶梯称为“素数阶梯”。

1849年，高斯发现了“素数定理”。即，整数越大，阶梯高度（素数个数）越接近于根据一个公式所计算出的曲线高度。因此，当整数趋近无限大时，所出现的素数个数与曲线高度将趋近完全一致。

破解一个素数秘密

素数神出鬼没，变化无常。高斯在貌似不规则分布的素数中，成功发现了素数的分布规律，提出了素数定理。借助于素数定理，我们不必一个一个地数数，就能在一定程度上准确预测素数的个数。而且，数值越大，准确度越高。

素数阶梯

这是一条由素数构成的“阶梯”。在整数列中，每出现一个素数，阶梯就升高一个台阶。在阶梯的某个地方，陆续出现了“59…61…67…”等较窄的台阶，在另外的地方则出现了“113……127…”等宽阔平缓的台阶。由此可见，这些台阶的分布极不规则。

整数数值越大，素数阶梯的高度越趋近于某一光滑曲线的高度。高斯提出的“素数定理”，可以用公式表示这一现象。

（本文发表于《科学世界》2013年第6期）