互动科普

惊人大发现！距离越远的星系离开我们的速度越快！

宇宙正在膨胀。接近这个惊人事实的第一步需要追溯到20世纪的10～20年代。当时美国的维斯托·梅尔文·斯里弗（Vesto Melvin Slipher，1875～1969）对大量星系进行观测并发现，我们居住的太阳系所在的星系（也就是银河系），其附近的星系明显没有远处的星系数目多。

1929年，美国的埃德温·哈勃(Edwin Hubble，1889～1953)对大量星系的距离和速度进行了测量，发现了一个惊人的事实：距离越远的星系离开我们的速度越快。星系远离的速度（退行速度）与到地球（银河系）的距离成正比。也就是说，如果星系A的距离是星系B的距离的两倍，那么星系A的远离的速度就是星系B的两倍，星系C的距离是3倍的话，远离的速度也变成3倍。这被称作“哈勃定律”。

图1.哈勃定律

我们并不能观测到星系的“移动”

当听到“测量速度”时，我们容易想到在一定的时间内测出星系移动的距离，然后距离除以时间就等于速度。但是星系距离我们非常遥远，所以很难测量星系自身移动了多少。实际观测的是“星系发出的光的波长（颜色）的变化”。所谓波长就是波的两个波峰之间的距离。

大家都应该有过这样的经验：救护车驶向我们时笛声听起来更尖，而远离我们时笛声变得低沉。这是因为接近时救护车发出的声波的波长变短（音调变高），远离时发出的声波的波长变长（音调变低）造成的。这一现象就叫做“多普勒效应”。

光也有类似的现象。当星系接近我们时，光的波长变短，远离时波长变长。“波长变短”对于可见光来说意味着颜色变蓝，反之，“波长变长”意味着颜色变红。因此，哈勃发现的正是，距离越远的星系看起来变红得越厉害（称作“红移”）。

大爆炸是发生在地球的位置上而把星系向四外吹散的吗？

从地球（银河系）上看，越远的星系正在以越快的速度远离我们，也就是遵循“哈勃定律”，这究竟意味着什么呢？

难道是“在很久以前地球现在所在的位置上发生了大爆炸，所以大量的星系（或者组成现在这些星系的物质）会向四面八方飞散开去？”至于越远的星系退行的速度越高这一点，一个看起来说得通的解释是：“在一开始爆炸时，星系（物质）受到了非常强的力的作用而被加速，所以速度越快的星系跑得越远”（至于星系受到的力的大小为什么不一样则需要考虑额外的因素）。实际上，关于宇宙诞生的“大爆炸”，持有上面说法的人非常多。

地球不应该是“宇宙的中心”

这个乍看起来很合理的假说存在着致命的弱点。如果这个假说是对的，那么就说明地球（银河系）处在宇宙的中心这一极端特别的地方。

让我们大致回顾一下人类的宇宙观。很久以前，人们认为地球就是宇宙的中心，太阳，太阳系里的行星，甚至系外恒星等都在围绕着地球分布。这也就是“地心说”。但后来人们终于认识到地球也不过是太阳周围的一颗行星而已。

到了18世纪后半叶，人们已经认识到太阳也不过是圆盘状恒星集团中的一颗，而这个集团就是银河系。银河系的直径大约有10万光年（1光年是指光传播一年所走的距离），太阳系是在距离银河系中心2.6万光年的位置上。同时每两亿年绕银河系“公转”一周。也就是说，太阳系也不是宇宙的中心。

如此说来，科学家们更相信“我们所处的位置在宇宙中并不特殊”。这个想法被叫做“宇宙学原理”。认为地球（银河系）处于宇宙爆炸中心的假说明显是违背宇宙学原理的，因此科学家们一般不采用这一观点。那么，科学家心中是如何构造一个满足哈勃定律的宇宙学图像的呢？

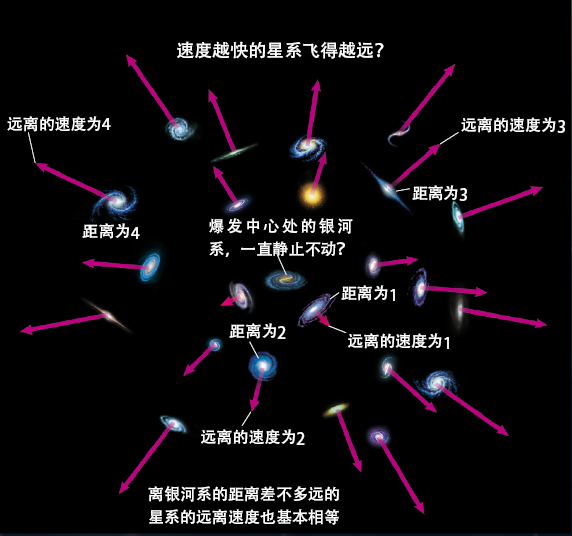
图2. 银河系位于大爆炸的中心吗？

如果宇宙处于膨胀之中，就能解释越远的星系退行越快的现象

实际上在哈勃定律发现之前的1922年，俄国物理学家亚历山大·弗里德曼（1888～1925）就从理论上指出：“空间可以膨胀也可以收缩”。也就是说，宇宙膨胀的观点足以说明哈勃定律。之后“宇宙在膨胀”就得到了科学家们的支持。

弗里德曼使用的理论正是阿尔伯特·爱因斯坦于1915～1916年间发表的广义相对论。在这一理论中，空间可以弯曲、膨胀和收缩等等。也就是说，空间不仅可以包含实体物质，而且本身会有“大小”和“形状”。

只要认为宇宙空间在膨胀，就能够很好地解释哈勃定律。为了简化说明方法，我们想象有很多星系沿着一条直线排列着（如下图A-1），它们都被固定在一条可以伸缩的橡胶带上（1维）。这条橡胶带就代表着宇宙的一部分（而不是表示宇宙的全部）。此外，图上还画有很多网格（辅助线），可以方便表现星系移动的距离。网格不随橡胶带的伸缩而变化。

考虑橡胶带出现伸长的情况。A-2与A-1相比橡胶带伸长了两倍。首先以银河系为原点，看看其他的星系会怎样变化。在A-1中，从银河系看来，星系A在左边2格的位置上，而在A-2上变成了4个格的位置，即移动了2个格。在A-1中的银河系右边3个格处的星系B在A-2中变成了6个格的距离。也就是说同样的时间里移动了3个格的距离。因此，星系B远离银河系的速度是星系A的1.5倍。

A-1中，从银河系看，左边第4格的星系C变到了A-2中的第8格。也就是在确定的一段时间里移动了4个格子的距离，所以星系C的速度是星系A的2倍。以上的分析可以总结如下。

·星系A → 原来的距离为2，退行速度为2

·星系B → 原来的距离为3，退行速度为3

·星系C → 原来的距离为4，退行速度为4

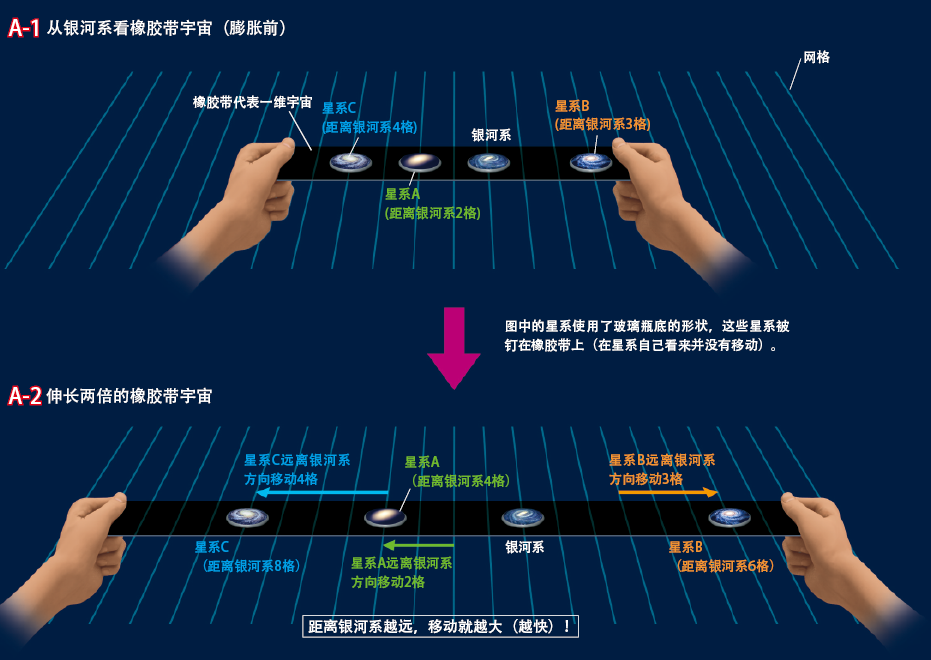
图3.从银河系看橡胶带宇宙

接下来我们采用星系A的视角来观察（B-1，B-2）。考察的顺序不变，只把结果写在下边：

·银河系 → 原来的距离为2，退行速度为2

·星系C → 原来的距离为2，退行速度为2

·星系B → 原来的距离为5，退行速度为5

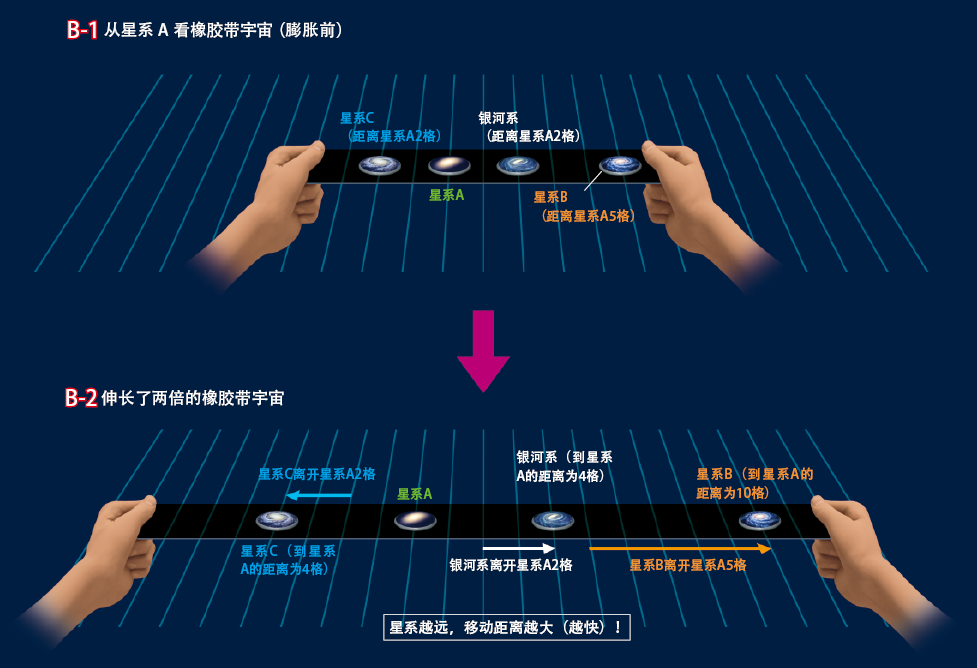
图4. 从星系A看橡胶带宇宙

正如上面所示，无论从银河系看去，还是从星系A看去，距离与退行的速度总是成比例的，这也就能理解哈勃定律了。利用橡胶带的例子，离得越远看起来远离得越快的原因就来自于空间伸长的“累加”。这样，星系B也好，星系C也好，无论从那个星系看去哈勃定律都会成立。在这样的宇宙学模型中不存在特殊的星系。

膨胀的速度有多快？太阳系也跟着膨胀吗？

宇宙膨胀的速度有多快呢？根据天文学上的观测，目前已知“到地球的距离每增加500万光年，速度就增加100千米/秒”。由此计算可得，距离地球1000万光年的地方，星系的速度是200千米/秒。这个速度还是很惊人的。

另外，“光年”是距离单位。1光年就是以光速（每秒30万千米）行进1年的距离，大约是94600亿千米。

太阳系所在的银河系的直径大约为10万光年（946000万亿千米），其他的星系也差不多这么大。假设在500万光年的地方有一个星系，其远离我们的速度为100千米/秒，这对于直径10万光年的星系来说，每秒钟不过移动了它的直径的9460万亿分之一而已，这就是所谓星系的运动。星系退行速度说起来很大，实际上对于星系的尺度来说，不过是移动了非常微小的距离罢了。

另外根据哈勃定律，太阳与地球之间的距离约为1.5亿千米，由此计算出地球相对太阳以每秒320纳米（每秒3.2毫米的万分之一）的速度远离而去。原子的尺度大约是0.1纳米，所以从太阳看来，地球每秒钟远离的距离只等效于几千个原子排在一起的尺度。从太阳系自己的尺度看，宇宙膨胀的效果可以说微乎其微。

实际上太阳系和原子都不膨胀！

虽然宇宙膨胀效应非常微弱，但是经过长年积累的话，太阳系是否也会被拉开呢？更进一步说，我们的身体以及构成身体的原子是不是也会膨胀呢？假若世界上所有的东西都以同样的速度膨胀，距离和测量的尺子同时膨胀的话，我们还能测量到宇宙的膨胀吗？

这个问题的结论是：实际上太阳系并不会膨胀。太阳和地球通过万有引力相互吸引在一起，引力的作用比起让太阳和地球分开的宇宙膨胀的“力”要强的多得多。因此太阳和地球之间的距离不会因为宇宙膨胀的影响而拉长。星系也是这样，通过引力场而紧密结合在一起的天体等也是这样（在前面我们用橡胶带和橡胶板来表示膨胀的宇宙，用瓶底来表示星系。这就是说，宇宙虽然在膨胀，但是星系的大小不会因此而变化）。

那么原子会发生膨胀吗？在原子的中心存在带正电的原子核，其周围分布着带负电的电子。原子核的大小只有原子的10万分之1，即使这样，原子核的尺度还要比电子大得多。想想原子的图像，难免会问，原子是否也会由于宇宙的膨胀而膨胀。

不过原子中的原子核与电子在电磁力的作用下紧紧地结合在一起，远远大于宇宙膨胀的作用，所以原子不会因为宇宙的膨胀而变大，我们身体里有无数的原子，它们在化学键的作用下牢固地结合在一起，所以也不会跟着宇宙的膨胀而变大。

那么什么东西会受到宇宙膨胀的影响而膨胀呢？

实际上宇宙膨胀导致的分离情况，只能发生在相互作用弱到几乎感觉不到的物体之间，比如距离遥远的星系之间。所以人类在很长的时间内没有意识到宇宙在膨胀也就没有什么奇怪的了。

（本文发表于《科学世界》2016年第11期）