互动科普

我们能够观测的宇宙只是整个宇宙的一部分

宇宙在膨胀，这就意味着过去的宇宙比现在要小，那么继续沿着时间回溯，最终宇宙的尺度就会变成零。数值上，宇宙的尺度为零的时刻要使用现在宇宙膨胀的速度进行推测。根据最近的天文学观测，宇宙的年龄有138亿岁了（更加正确的说法是，宇宙膨胀的速度在宇宙的历史中是一直变化着的，所以只使用今天的膨胀速度是不能正确求解出宇宙的年龄的。不过大致的年龄是可以得到的）。

另一方面，使用望远镜等设备所观测的宇宙本质上是光（电磁波）。光的速度大约是每秒30万千米。虽然这是一个非常惊人的速度，但毕竟是一个有限的数值。比如说，太阳与地球之间的距离有1.5亿千米，走过这段距离光要花上大约8分钟。而临近的恒星（半人马座比邻星）大约有4光年远，也就是说光也要4年的时间才能到达。

宇宙的历史有138亿年，也是一个有限的长度，这一期间光所能前进的距离因此也是有限的。因为光是自然界中速度最快的，所以对于138亿年中光所能到达的范围之外的宇宙，从基本原理上来说就是不可观测的。这里强调“基本原理”是指无论技术多么先进发达，都不能观测的意思。

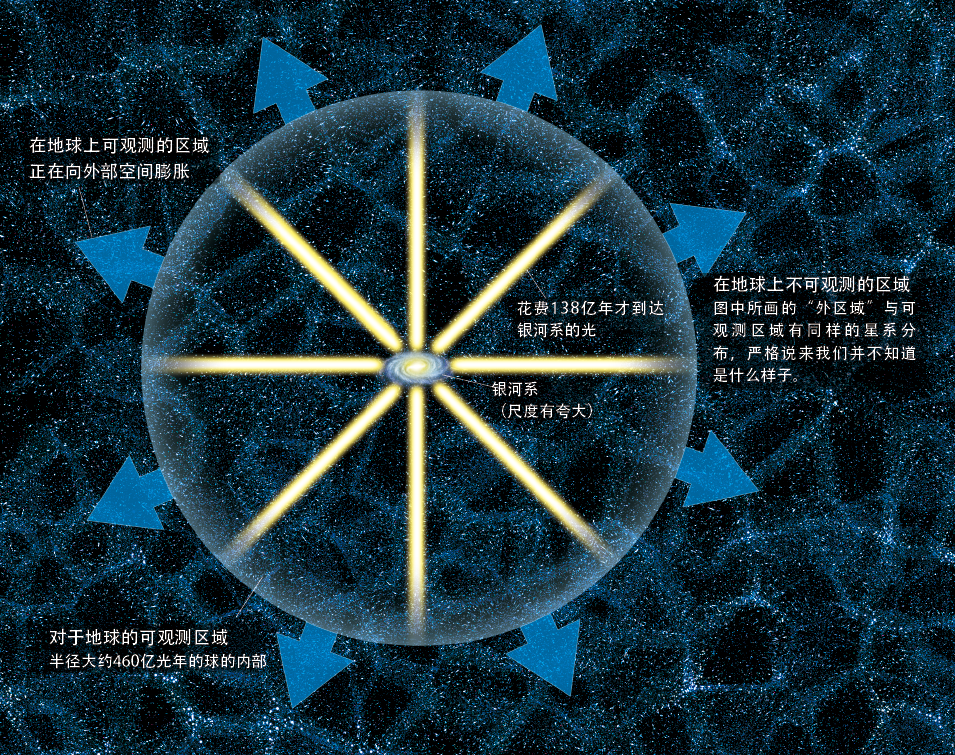
图1. 可观测区域与“外”边的宇宙

在观测无法到达的区域之“外”只能进行理论上的推测

可观测区域是以地球（银河系）为中心呈球形。如果持不可观测区域已经超出了科学的范畴这种谨慎的立场的话，所谓宇宙只能是这个球内的区域。如此说来，宇宙应该是向着更“外”边的空间膨胀着。

如果扩展一下宇宙学原理的思路到可观测区域的“外”部，不难想象那里的环境也会和银河系周围相差不多吧。

严格说来，宇宙的膨胀也只能在可观测区域内进行验证，在其外部是否也在膨胀我们并不知道，也可能并不膨胀。但是一般都认为，可观测区域的外部也和可观测区域内一样在膨胀。

如果宇宙是有限的，宇宙向着什么地方膨胀？

接下来我们开始一起思考包含可观测区域之外的全部宇宙（相连的全部空间）。

当然因为观测不到，只能从理论上进行推测。关于全部宇宙，理论上有两种可能性。宇宙的尺度（全部空间的体积）可能是有限的，也可能是无限的。我们现在考虑有限的情况。

即使是一个有限大小的宇宙，物理学家们也不会认为空间会在某个地方突然结束，从而有一个不自然的边界。比如立方体的展开图就具有边界。如果把这个图形卷起来，并把相关的边界粘起来（关闭起来），就组成了面积有限而且没有边界的立方体表面。地球的表面也构成一个“球面”，它就是面积有限但没有边界。这就是2维的球面，弯曲而闭合。

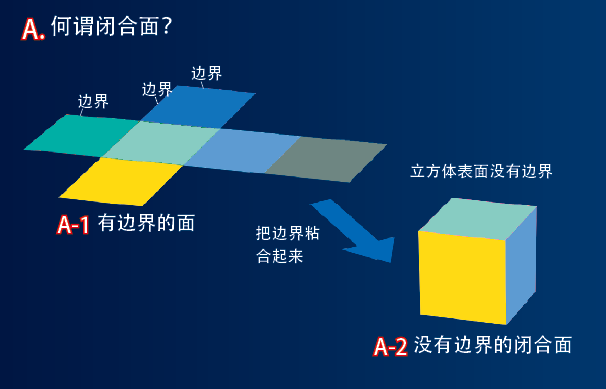
图2. 何谓闭合面

根据爱因斯坦的广义相对论，3维空间也可以是弯曲的。在大质量的天体周围空间发生很大的弯曲。实际上，当光在太阳旁边通过的时候确实会稍微发生一点偏折。光在真空中一定是沿着最直接（最短）的路径传播。所以，与其说在太阳附近光本身发生了弯曲，不如说光在沿着弯曲的空间向前传播。这就是为什么在地球上观测光的轨迹的时候，看起来路线是弯的。

但遗憾的是，我们没法直接认识3维空间的弯曲，无法感知，也不能正确的画出弯曲的空间。可以画出来的只能是减少一个维度的2维球面，然后类推到3维空间去。理论上，宇宙有可能像一个球面那样缓缓弯曲而且闭合。在这样的宇宙中，就像沿地球表面一直“向前”传播的话，光会绕行一周回到原来的地方。但是究竟要走多远才能回到原来的地方我们并不知道。

对于弯曲闭合的3维宇宙，就像全部球面没有边界一样，也就不能考虑它的“外部”了。因此，人们经常会问的“宇宙在向哪里膨胀？”也一样变得没有意义。另外，因为没有边界，也就没有宇宙膨胀的中心了。

宇宙也可能是无限的

下面我们来看一下弯曲空间的另一个侧面。为了可视化弯曲的空间（3维），与之前2维球面的方法相同，还是减掉一个维度。

即使是在球面上，也可以定义“直线”。但这时的直线说的是“球面上两点之间沿着球面的最短路径”。这一路径就是某个球大圆，它是通过球心的平面与球面相截的曲线。在地球的表面上，经线和赤道（纬度为零的纬线）就是球大圆。而赤道之外的纬线因为不过球心，所以不是球大圆，也不能认为是“直线”。

接下来看一看球面上的三角形。三角形的各边都必须是球面直线（大圆的一部分）。在平面上的三角形，它的内角（两条边所夹角的内部）和正好是180°。但是，在球面上的三角形的内角和一定会大于180°。

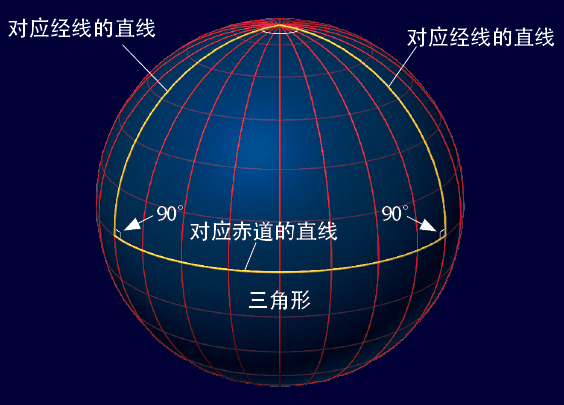
图3. 在球面上，三角形的内角和会超过180°

最容易理解的一个例子要算是两条经线与赤道组成的三角形了。经线与赤道所成的夹角一定是90°，也就是说两条经线和赤道分别所夹的两个角度加起来就足有180°了。而两条经线之间也一定会有一个角度，所以内角和一定会大于180°。

同样地，在闭合弯曲3维空间中的三角形，其内角和也会超过180°（这样的弯曲空间被称为“正曲率空间”）。也就是说，如果想要知道宇宙空间的弯曲程度的话，只要在宇宙中测量一个巨大的三角形的内角和就可以了。

可观测范围内的宇宙基本上是平直的

即使在弯曲的空间中画出一个三角形，也必须要有三条“直线”来构成边。空间中的直线可以使用光来充当。因为前面我们也说过，光在真空中一定是沿着最直接（最短）的路径传播。由于更加具体的内容很难在这里展开，不得不省略一部分，实际上这样的情况在天文测量上是可以实现的。但使用的不是人造的光源，而是利用来自宇宙深处的光。

现在我们知道测量的结果是三角形的内角和基本上为180°。换句话说，在可观测的范围内，宇宙几乎没有弯曲，基本上是平直的。但是，在现在的观测技术还不能确认的区间内，宇宙还可以有一点点的弯曲，所以还不能完全否定掉闭合宇宙的可能性。

如果宇宙是完全平直的（也被称为“零曲率空间”），那么在这样的宇宙中，不会发生空间突然停止延展，从而形成边界这种不自然的事情。对于这种宇宙，人们自然认为是（体积）无限大的。

理论上宇宙也可以弯曲成三角形内角和小于180°的情况（这样的弯曲空间称为“负曲率空间”）。这样的空间很难在3维中描绘出来，其2维的情况对应于鞍面。很自然地，这样的宇宙也是无穷大的。

以上说的具有无穷大空间的宇宙被称为“开放的宇宙”。

无穷的宇宙中无法确定“膨胀的中心”

无穷是一个不可思议的事情。假如把无穷也看成是一个数的话，无论在无穷大上加了多大的数字，还是无穷大（∞+a=∞，a为正数，以下相同），无论减掉多大的数字也是无穷大（∞-a=∞）。做乘法和除法也是一样（∞×a=∞，∞÷a=∞）。所以与我们日常所接触的数字相比，无穷大实在是非常不同。

如果宇宙是无穷大的，那么就不应该问“宇宙在向什么地方膨胀？”这样的问题了。没有比无穷大更大的数字，也就没法想象一个无穷大体积宇宙的“外”部。无法确定零和无穷的“正中心”，也就无法决定无限宇宙的膨胀中心在哪里了。

为了感受一下无穷的不可思议，让我们想象一下骰子。准备10个骰子，它们全都出现1的概率为60466176分之1。也可算得上是极低的了，但还不是零。如果把这个试验进行无穷多次的话，10个1的情况一定会出现，而且会出现无穷多次。

同样地，在无穷大的宇宙中，只要发生的概率不是零，就会发生无穷多次。比如宇宙中存在非常像地球的行星，上边有个非常像你的人，而且这样的行星有无数颗。

地球或者你自己说到底也是由无数个原子按照特定的排布组成的。如果能够排出同样的原子的话，地球也好、你也好，都能够复制出来。因为地球和你在今时今地存在的概率不是零，所以算起来在无穷宇宙的某个地方可以存在同样的原子排列，从而会有无穷多个副本。

这个奇妙而无限的宇宙真的可能存在吗？虽然听起来很难相信，松原博士却说：“一个有着自己分身的世界确实奇妙，但是作为物理学家，不能只因为‘奇妙’，就否定掉这种宇宙的图像。

（本文发表于《科学世界》2016年第11期）