互动科普

六色同堂图案知多少？

自从魔方皇后推出“六色同堂、四角同色”图案以后，许多魔方爱好者致力于发现新的六色同堂图案。但几十年来，这方面的进展并不大，见之于文献和网络的新的六色同堂图案只有寥寥几个。下面的“六彩方中方”算得上是另外一个比较美丽的六色同堂图案，见图2。

图2. “六彩方中方” 图案

这个图案，在3×3×3的魔方前左上角和后右下角各有一个2×2×2的小魔方，小魔方的4个面是同色的，而其周边5个小面恰为另外的5个颜色，因而也是六色同堂的！应该说，其构思很有特色且富于创意。但是实现这个图案的操作十分复杂，需要59步：

R  U  (F  U  D′ )2  L  U  D′  B  U  D′  R  F′

D  F′  U  D′  L2  D  U′  F′  U′  D′  R′

D′ (B2  L2)2  B2         

L′  F′  L′  F  L  F′  L′  F  D  (F′  L  F  L′ )2

F2  U  F2  L2  U′ F  U2  F2  U2  F′ U  L2

因此，许多人认为六色同堂图案不多，而且很难实现。情况真是这样么？我们认真分析了这个问题后，推翻了这个结论。

为了说明问题，我们先用6元组定义六色同堂图案，6元组中的6个元素表示6种颜色，其值表示具有该颜色的小面有几个。在这种定义方法下，六色同堂图案只有以下3种类型：

第一种类型，（4，1，1，1，1，1），表示有同色小面4个，其他5种颜色各有一个小面。以上介绍的“六色同堂、四角同色”图案和“六彩方中方”图案就都属于这一类型。

第二种类型，（3，2，1，1，1，1），表示某种颜色有3个小面，另外一种颜色有2个小面，其他4种颜色各有一个小面。

第三种类型，（2，2，2，1，1，1），表示有3种颜色各有2个小面，其他3种颜色各有一个小面。

除了以上3种六色同堂图案以外，不可能有其他类型的六色同堂图案了。

在第一种类型的六色同堂图案中，根据4个同色小面的分布情况，又有许多子类型。可能的子类型有23种，如图3所示。

图3. 第一类六色同堂图案可能的子类型

显然，魔方皇后的“六色同堂、四角同色”图案属于其中的第20小类，而“六彩方中方”图案属于其中的第5小类。

第二类和第三类六色同堂图案可能的子类型就更多了。拿第二类来说吧，3个同色小面的分布情况就有16种；对其中的每一种，2个同色小面又有许多可能的分布情况。第三类的情况类似。据我们统计，第二类有174种子类型，第三类有178种子类型。限于篇幅，我们不给出具体图案了。

以上分析中，我们都说“可能”图案，因为这样的图案是否存在是不一定的。目前我们还不能从理论上去证明哪种图案是可以实现的，哪种图案是不可以实现的，我们只能尝试着去找到各种各样的六色同堂图案。值得高兴的是，经过一段时间的摸索，我们已经找到了许多六色同堂图案的实现途径。下面，我们就把我们已经发现的部分六色同堂图案介绍给大家，请大家欣赏。实现这些图案的操作序列只采用外侧面旋转，而且都不到20步。

第一类23种六色同堂图案，我们都已实现。作为例子，我们给出第2、4、5、7、15、19、20、23这几种，见图4。

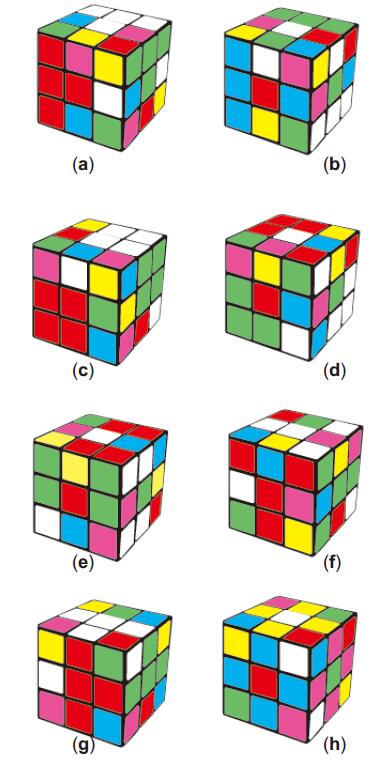
图4. 第一类六色同堂图案示例

实现这些六色同堂图案的操作序列如下：

（a）U2  L2  B2  U2  B2  R  F  R2  B2  U2  R′  B′  U′  B  D2  U′  B  D  B2

（b）B2  L  F2  D2  R′  B  U′  F′  R  D′  L2   B′  L′    B2  D′  B2  D2  R2

（c）F2  U2  B2  U′  L2  U′  L  F2  D2  U′ F  R  D  R2  F′  U

（d）L2  U2  B2  L  R2  B  D  B  L  B  U′  L′  R′  U2  B  F′  R2  D′  U′  R2

（e）R D L′  F  U  R  F  B′  D′  F′  B2  D′  R2  L2  F2  U2  F2  B2  U2  L2

（f）R2  B2  D′  U2  L2  U2  B2  R2  B′  L′  F R2  B2  D2  F  R2  F′  L2  F′

（g）R2  F2  R2  D2  U2  F  U  L  R2  B2  D  L2 U  F  L  U  F  D′  F′

（h）U2  L′  D′  F  L2  D  R  F2  U2  D  B  R  U′  L  F  B2  R′  F2  L

其中，图案（c）也是“六彩方中方”，我们只用了16步。最后这个图案（h）也很有名，就是所谓“六色同堂、四边同色”。这个图案以前也有人实现过，但操作序列很长，我们这里只用了19步。

下面介绍几个第二类，即（3，2，1，1，1，1）类型的六色同堂图案，也选择两种同色小面的分布比较对称，因而比较美观的几个，见图5。

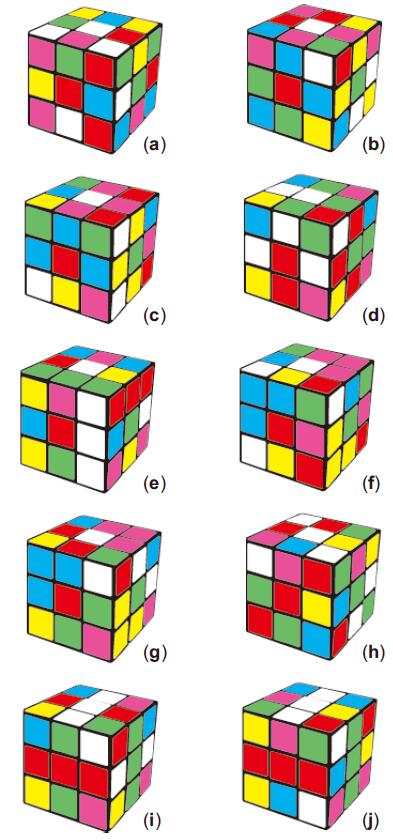
图5. 第二类六色同堂图案示例

实现这些图案的操作序列如下：

（a）U′  R2  U2  R′ U  L  B2  U  F  L′  B  U2  L  D  B2  D2  R2  U2  R2

（b）B2  F′ U2  L2  R2  F2  D2  U′  B   R′  D′  L′  F  R2  U2  F′  U  R2  B  L′

（c）B2  F2  L2  R2  D  U2  F′     U  L′  B′  D′  L′  R  F  L  R2  F  R2  U2

（d）B2  F2  D2   L2  U  B′  L2   F2  U  F  U  R′  U′  L  D′  L′  D2  B′  F2

（e）F2  U2  R2  D′  U′  F2  R2  U′  R2  B′  F U2  L′  F  U2   L′  R  F2  U′   F2

（f）L2  D  B2  L2  U′  R  F  D  L  B′  L  F2  D  F′  R2  F  L  D2  R

（g）R  U2  L  R′  D2  U2  F′  U′  L′  D′  R  F′  U2  L′  B2  D  U2  F′  R

（h）F  D2  U2  B′  U2  L2  F′  L  B′  R2  U′  B  R2  D  U2  L′  D  R  U′  F′ 

（i）U2  L2  U2  B2  F2  U  B2  L′  D2  B  D   U′  R2  B2  L′  D  B  D′  B′  U′

（j）D2  L2  R2  F2  D2  L′   F′  U  L2  U′  L U  L′  F  L′  D2  F  U  R

类似地，我们给出第三类，也就是（2，2，2，1，1，1）类型的几个六色同堂图案作为示例，见图6。

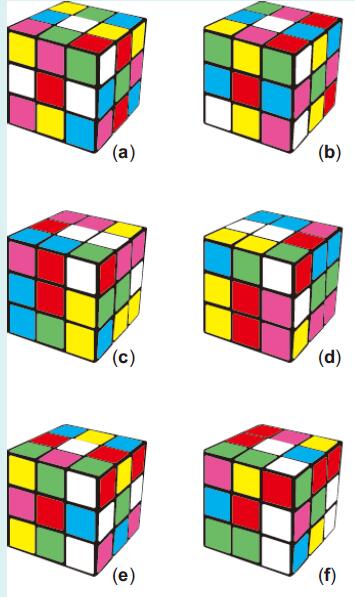
图6. 第三类六色同堂图案示例

实现这些图案的操作序列如下：

（a）L2  D  B2  R2  U  B2  F′ U  B  F2  L2  D′  U2  L  F′ D  R  U′   F  D′

（b）D  L2  D2  F2  D  L2  U2  B  L′  U2  F2  D U  R2  B  L  R  D  F′  U2

（c）D′  L2  D′  R2  U  F′  L  B2   U′  F  R2  F′  R′  F  L′  U  R  D  R′

（d）R2  U2  B2  L2  D′  U′  B2   U   L′   B′  L′  B2  F2  D′  R  B2  U2  F

（e）L2  D2  R2  D  R2  B2  R2  D  U′  L  R′  U′  R′  F′  D  U′  R  B  D  F

（f）D2  B2  D2  L2  U  B2  F  U2  B′  L′  B′  L2  D  R′  B  F  U2  R′  F2  U

（本文发表于《科学世界》2011年第5期）