互动科普

几点进一步的讨论

前面我们在讨论魔方六色同堂图案的分类时，用了大类、小类的概念。由于魔方运动的随意性，魔方6个面上的图案可以像“万花筒”那样千变万化，因此同一小类也可以有许许多多不同的图案。例如，图4（c）我们给出的是第一大类第5小类的一个图案，这类图案中每个外侧面上的4个同色小面紧紧挨在一起，形成一个正方形。但每个正方形在其外侧面上位于什么位置是可以变化的。在图4（c）中，3个共顶角的外侧面上的3个正方形又紧挨在一起，因此形成“方中方”。现在我们看下面这个18步的操作序列：

U′   L2  D2  U  F2  U2  F′  L  D2  L′  F  U′  B  R  U  B′  U  F

它形成的魔方图案如图7所示。

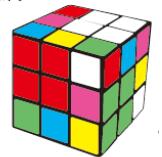
图7. 第一大类第5小类的另一个六色同堂图案

在这个魔方图案中，6个外侧面上由4个同色小面形成的正方形，没有两个是共一条边的，因此不形成“方中方”。乍看起来，图4（c）和图7这两个魔方图案是如此不同，但它们却是属于同一小类的。其他小类也有类似情况。

同一小类的图案，即使同色小面在每个外侧面上的位置完全相同，其他只有一个小面的各个颜色的分布仍然可以大不相同。请看我们用以下两个操作序列所形成的两个魔方图案（图8）：

图8. 第一大类第2小类的2个六色同堂图案

（a）U2  L2  B2  U2  B2  R  F  R2  B2  U2  R′  B′  U′  B  D2  U′  B  D  B2

（b）U2  B2  L2  D2  U2  L  U2  R2  D2  B′  R2 B  F2  R2  F′  U′  R2

从右前方看这两个魔方，顶面和右面的图案完全一样，前面的图案也基本相同，惟一的区别是蓝色小面和粉色小面的位置恰好对换了一下。从左后方看这两个魔方的情况类似。造成这种差异的原因是操作不同，因而边块的循环置换不同，如下所示：

（a）:（uf，dr，bl，lu，rf，db）（ur，ub，rb)+ (df，lf，ld)+

（b）:（uf，dr，bd)+ (ur，ub，rb)+ (ul，fr，fl，dl，df，lb）

上式中，括号后右下角的加号表示括号中最后那个边块在置换括号中第一个边块的时候要发生翻转。

以上我们看到的所有六色同堂魔方，6个表面上的图案都是完全一样的，都限于同一大类，而且是同一大类中的同一小类。这样的魔方图案，我们称之为“纯种”的。当然还可以有6个表面上的图案不一样的情况，也就是“杂交”的图案。“杂交六色同堂”又可分以下几类：

六面同一大类，但有不同小类。我们把它称为“杂交1号”。

六面分属不同大类，但有相同小类。我们把它称为“杂交2号”。

六面分属不同大类，并有不同小类。我们把它称为“杂交3号”。

图9中我们给出这3种杂交六色同堂图案的示例。

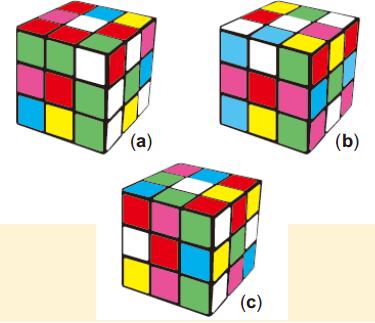
图9. 杂交六色同堂图案示例

图9（a）是杂交1号六色同堂图案，6个面都是（4，1，1，1，1，1）类型的，但前后面和左右面、顶底面属于不同的小类。图9（b）是杂交2号六色同堂图案，其顶、底两面是（3，2，1，1，1，1）类型的，而其他4面是（2，2，2，1，1，1）类型的。图9（c）是杂交3号六色同堂图案，因为它只有右面是（3，2，1，1，1，1）类型的，其他5面都是（2，2，2，1，1，1）类型的，但3组两两同色小面的分布各不相同，属于不同小类。

实现图9中几个杂交六色同堂图案的操作序列如下：

（a）R2  F  R2  B′  U2  B  R2  B  U2  L2  U  B2  L  R  F2  L2  B′  F′

（b）F  B  R  L  F  B  R2  L2

（c）F2  B2  R2  L2  D′  U′  F  L′  B

通过以上讨论，我们可以看出，小小魔方中蕴含着许许多多有趣的问题，值得我们去探索、去发现，我们愿意同广大的魔方迷一起努力。有兴趣的读者可通过以下电子邮箱和我们交流：Mohailiang1984@sina.com  Wuhl1937@sina.com

（本文发表于《科学世界》2011年第5期）