互动科普

高温的物体为何会发出明亮的光？其机制也与量子论的诞生有关

在19世纪即将结束的时候，为了冶炼出高品质的钢铁，人们需要能够正确地测量出熔炉中的温度。由于冶炼炉的温度太高，不可能在炉中放入温度计来测温。所以实际使用的方法是观察高温物体所发出的光（波长)，进而推测其温度的高低。红色对应600℃左右，黄色对应1000℃左右，白色对应1300℃以上的温度。

但是对于物理学们来说，这成了一个大问题，因为无法从理论上解释高温物体的发光规律。直到德国物理学家马克斯·普朗克（1858～1947）在1900年得到了和实验结果一致的方程才算有了一个恰当的解释。仔细地考查这个方程，我们可以发现普朗克革命性地提出了所谓“量子假说”。

周期性地按压水面上飘着的球，就会在水面上产生波。同样的道理，原子、分子在振动的时候也会发出光的波（电磁波)。普朗克的量子假说认为，“发出光的粒子振动的能量只能取一些分立的数值。”

我们试着用弹簧的振动来理解普朗克的假说。在量子论出现以前，振动着的弹簧所携带的能量决定于弹簧的最大振幅相对于原初长度的伸长量。那么根据普朗克的假说，这个最大伸长量只允许取一些分立的数值，而在这些数值之间的振动模式是不允许存在的。

能量的变化是不连续的，这对于量子论出现之前的时代来说是非常奇妙的事情。不过普朗克认识到，要想得到与实验相符的方程，就意味着不得不让能量分立地变化。

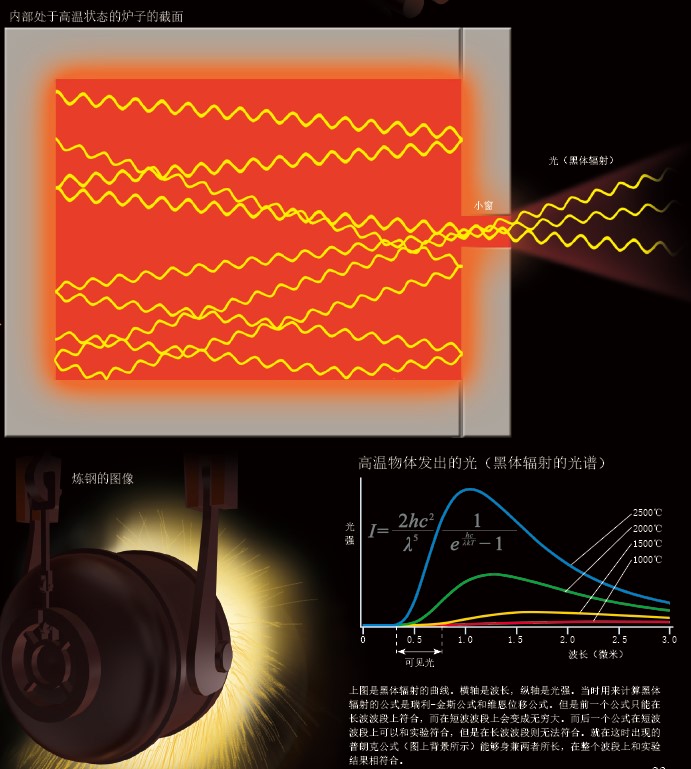
 “量子假说”诞生于高温炉中的发光现象

从高温炉的小窗透出的光在出来之前已经在炉壁上反射过多次。像这种从“空腔辐射”出的光被称为“黑体辐射”。

横轴表示从小窗发出的光的波长，纵轴表示对应波长的光的强度。这条曲线的形状是不依赖于炉子的材料和形状等因素的，只决定于其温度（右下图）。反过来想，可以通过测量光来推测其内部的温度。普朗克正是反复研究这条曲线之后才提出量子假说的。

爱因斯坦的惊人发现——“光是粒子”，其证据就隐藏在日常生活中

在德国出生的物理学家阿尔伯特·爱因斯坦（1879～1955）也独立地考查了高温物体发出的光。普朗克发现发光粒子的振动能量是分立的，而爱因斯坦在1905年提出的假说与普朗克的稍有不同。

这就是光量子假说——“光的能量是一份一份的”。这意味着光是由具有粒子性质的“光子”(也就是光量子)集合而成的。

光是不连续的光子的集合，这与我们的日常生活有着深刻的联系。比如说，我们之所以能看到夜空中的星星，就是一个光子集合的例子。

夜空中闪耀的大部分星体是与我们的太阳类似的“恒星”。其中最近的恒星离我们地球也有约4光年远，所以夜空中的星星皆处在异常遥远的地方。

正是因为光具有粒子的性质，所以我们才能看到夜空的星星

距离光源越远，看起来光源也就越暗。当距离变成两倍时，亮度变成1/4（2的平方分之1）。亮度和距离的平方成反比。

假如光是连续的，就可以在空间中均匀地传播，也就是可以被无限地摊薄。由于夜空中的星星非常遥远，当光到达我们眼中的时候已经被摊得非常微弱，以至于无法我们的视网膜上的感光分子，也就是说我们将根本看不到星星。

不过，光作为光子的集合又会怎么样呢？从光源发出的光子密度（单位体积内的粒子数）虽然会降低，但是每一个光子本身将保持自身的能量。光的能量也就不会被无限地摊薄了。因此，光子打到视网膜上的时候，还有足够的能量让我们看到星星。

（本文发表于《科学世界》2013年第9期）