互动科普

使用对数简化计算是必须使用常用对数表的。计算尺的刻度如果没有常用对数表也是刻不出来的。可是在发现对数的当时，不用说，在这个世界上也还没有对数表。

也就是说，对数的发明者纳皮尔是通过手工计算计算出对数的，因为只能从0开始制作对数表。纳皮尔通过庞大的手工计算，终于在1614年发表了名为《奇妙的对数表的描述》（Mirifici logarithmorum canonis descriptio）的论文，从他开始研究对数起，花了整整20年。

然而，纳皮尔研究的对数并不是以10为底数的。从简化计算的观点出发，为了容易调整位数，底数为10是最方便的。开始研究以10为底的对数（常用对数）的是英国的数学家亨利·布里格斯（Henry Briggs，1563～1630）。布里格斯受到纳皮尔论文的启发，拜访了纳皮尔，交换了关于对数的意见，提出了以10为底数的思想。

布里格斯在1617年出版了到1000为止的正整数作为真数的常用对数表，在1624年出版了以从1到20000和从90000到100000的正整数为真数的、计算到小数点以后14位的对数表。

换句话说，对于2到9的正整数，精度到小数点以后1～2位还能比较简单地求到其对数。因为首先2¹⁰⁼1024，1024和1000很接近，不妨让2¹⁰≈1000来看，两边同取对数log₁₀2¹⁰≈log₁₀10³。根据对数法则③和log₁₀10=1，就变成10×log₁₀2≈3，log₁₀2≈3/10 = 0.3。实际的值是0.3010…所以是非常相近的。

常用对数表的菜单

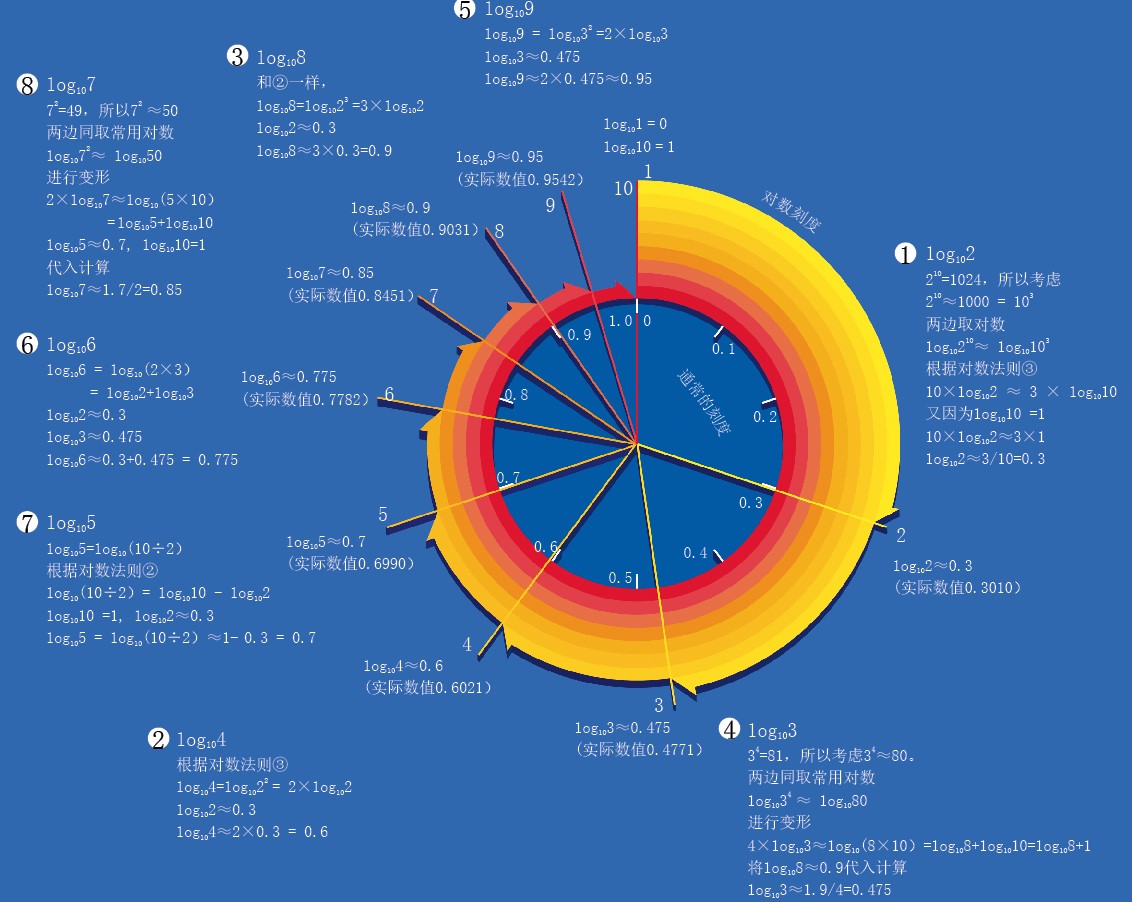
使用对数简化计算是必须使用常用对数表的。计算尺的刻度也是用常用对数表刻出来的。本图为简易制作常用对数表的方法。

插图中的圆，内侧的圆周上刻着通常的刻度（等距离刻度），而外侧的圆刻的是对数刻度。并且，因为10的0次方是1，即log₁₀1=0，对数的起始点（原点）是1。

（本文发表于《科学世界》2013年第11期）