互动科普

研究对数的目的几乎就是为了简化计算。在这个领域，对数发挥了巨大的威力，其结果奠定了科技发展的基础。

实际上，在对数的研究中，揭示了一个特别的数字的存在。这个数字，目前在数学和物理学中是以“主角”的级别出现的，这个数字就是“e”。

所谓的e，它本身只是一个普通的数字而已。具体地说，就是“2.71828…”。和著名的圆周率“π”（3.14159…）一样，e也是一个无法用分数表示的“无理数”常数。

发现e的是瑞士的数学家莱昂哈德·欧拉（Leonhard Euler，1707～1783）。欧拉是在把“对数函数”作“微分”的过程中发现了这个特别的数字e。“对数函数”和“微分”都是本文中第一次出现的新名词，下面略作解释。

什么是对数函数？

首先，“对数函数”是关于“对数”的函数。那么，函数是什么？比较通俗的一个类比就是，函数和自动售货机差不多。对自动售货机来说，只要按下某个按钮，与之对应的饮料就会出来。同样，在函数（自动售货机）中，只要确定了某一个数（按下某个按钮），按照函数的规则，和这个数值相关的另外一个数值（和这个按钮对应的饮料）就确定了。决定这两个数的关系的规则就是函数。

让我们来观察一下对数函数的具体例子。例如y=log₁₀ x这个式子。将100代入log₁₀ x的真数部分x中，就变成了y=log₁₀100，就决定了y=2。将1000代入x中，就决定了y=3。如此这般，某个数x和某个数y的关系由对数规则决定的时候，这个关系式就称作对数函数。

什么是微分？

下面看看“微分”。“作微分”通俗一点的解释就是，“求变化的比例”。例如开车。假设开着车子行驶了1个小时，1个小时行驶了多少距离就是速度。速度是距离随时间的变化，所以，对距离求微分就是速度。上面说的是1个小时内的平均速度。实际在开着车子行驶的过程中，只要知道每个瞬间的“行驶距离的变化值”，就知道了各个瞬间的速度。也就是说有了行驶数据，将它作一下微分，也就能再现每个瞬间的速度了。

那么，反过来考虑一下。也就是从已知的速度数据来重现行驶距离。相对于“距离→速度”的微分，“速度→距离”称作“积分”。虽然这里是用距离和速度来说明，但是微分和积分适用于生活中各种各样的“有变化的量”。

微分的思想，也许举函数图像为例大多数人容易明白。对原函数微分得到的新函数就是表示原函数的切线斜率的走势。

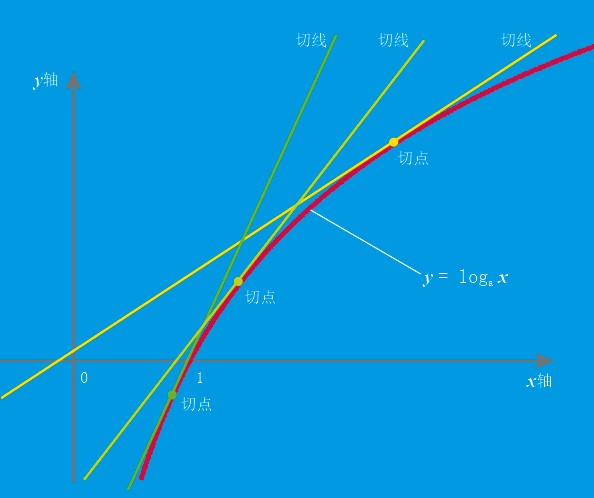
什么是微分？

以对数函数y=log_ax为例，认识一下微分。上图中红色的曲线是对数函数y=log_ax的图像。微分就是“求变化的比例”，这就是相当于求函数图像的“切线的斜率”。切线的斜率在不同的切点是不同的。对原函数微分得到的新函数，就是表示原函数的切线斜率的走势的式子。

世界上最美的公式

让我们回到e的话题。e是在对“对数函数”求“微分”的时候发现的。对对数函数y=log_a x求微分，就是x的值变化非常小的时候，求y的变化值。这个求变化比例的计算也是照着函数式进行的。

欧拉对数函数y=log_a x作微分，得到了

“y =log_a x微分后的式子”=（1/x)×log_a(1+h)^1/h。

其中h是一个无限接近于0的数。当h无限接近于0时，(1+h)^1/h无限接近于一个常数“2.71828……”，这个数就是e。

把这个数用e表示后的微分式就变成了“y=log_a x微分后的式子”=（1/x）×log_ae。这里考虑一下如果log_ae的底（也就是a）也是e的情况，log_ee=1。那么，当a等于e时，“y=log_a x微分后的式子”=1/x是非常简洁的。

对一个函数作微分得到一个非常简洁的公式，在微分计算中是非常重要的。最极致的是对y=e^x 这个被称为“指数函数”的函数作微分，有关系式“y=e^x  微分后的式子”=e^x成立。也就是说微分后的函数和原来一样。再说一句，这个式子作积分后e^x的部分也不变。

发现e的欧拉还留下了其他辉煌的业绩。这就是著名的欧拉公式。

e^ix = cosx + i sinx

这里出现的是欧拉发现的“e”和其自身平方等于“-1”的“虚数”“i”，还有“三角函数”cosx、sinx之间的奇妙的关系。并且当e^ix=cosx+i sinx的x的值等于π的时候，e^iπ=-1。这就是“世界上最美的公式”。

这里我们避免作太具体的解释。欧拉公式的本质是：通过虚数，将指数函数和三角函数联系起来。并且，指数函数成为容易微分和积分的e^x形式。这个简单的公式让一眼看上去毫无关系的这些部分联系了起来，并且在虚数这个世界里，指数和三角函数是可以互相转换的。

在物理学上对圆周运动、波动研究比较多，这种研究中使用三角函数比较方便。可是三角函数作微分和积分非常麻烦。欧拉公式的出现，使得做圆周运动、波动研究的物理学迈出了巨大的一步。这个贡献不仅阐明了我们身边世界中肉眼能够看到的物理现象，甚至影响到了研究微观世界法则的“量子论”。

纯粹以计算工具出现的对数，向人类展示了特别的数“e”的存在，使人类在知识领域的探险获得了飞跃性的发展。

（本文发表于《科学世界》2013年第11期）