互动科普

所谓“背囊问题”是考虑将背囊内放入多个物品的问题。背囊内可放入物品重量的最大限额已定好。此外，各个物品的重量和价值也是定值。在不可能将所有的物品都放入背囊内的条件下，如何进行组合，才能使装进背囊的物品的总值最大呢？

假设现有两种招财猫各1个，其中，价值10万元的红色招财猫重2千克，价值14万元黄色招财猫重3千克。用来装这些招财猫用的轻便背囊载重量为4千克，超过4千克的话，背囊就会漏掉。所以装进背囊的物品重量必须控制在4千克以内。那么要使所运物品的价值最高的话，应该怎样选择招财猫呢？在解这个问题时你是如何考虑的呢？是不是这样：“2千克和3千克，两者都放入背囊的话，就超出了背囊的容量（4千克），所以不能将两者都放入。那样的话，就在两个物品中选择价值较高的3千克的物品。”只是凭直觉我们就可以如此推导出来吧。

图1. 两种招财猫的轻便背囊问题

如果逐一列出可能的答案，什么时候可以得到正确答案呢？

将问题的解决方法变得稍稍严谨一些的话，可以考虑如下。首先是否可以放入2千克的物品呢？当然有两个选择。在“可以”或者“不可以”放2千克物品的基础上，分别又有两个选择：“可以放入3千克的物品”和“不可以放入3千克的物品”。也就是说，可以放入物品的组合一共是2×2=4个。在这4个组合中，选择在背囊容量内且价值最大的那个组合，就是这个问题的答案了。

每增加一个物品，可能的组合将增加一倍

那么，物品种类增加到5种的话会怎样呢？这种情况下，需要考虑的可能性为：是否放入2千克的物品（2个选择），接着是否放入3千克的物品（2×2，4个），然后是否放入4千克的物品（2×2×2，8个），接下来是否放入5千克的物品（2×2×2×2，16个），最后是否放入6千克的物品（2×2×2×2×2，32个），最后物品的组合一共是32个。每增加一个物品，会增加该物品放入或者不放入的选择项，所以当物品有n种时，就必须考虑2的n次方（将n个2相乘所得的数字）种组合方式。

图2. 要是有五种招财猫呢？

当n为5时（物品有5种），大概还没有问题。但是，如果n为10的话（有10种物品），物品的组合数就是1024；n为20的话（有20种物品），组合数为1048576；n为30的话（有30种物品），组合数为1073741824。物品的种类只要稍稍增加，计算量就会不断增加。

利用这样将所有的可能性都一一调查的“愚直”的方法的话，即使是使用高性能的计算机，也会发生因计算太过费事，以至于在现实可行的时间内无法推导出结果的状况。

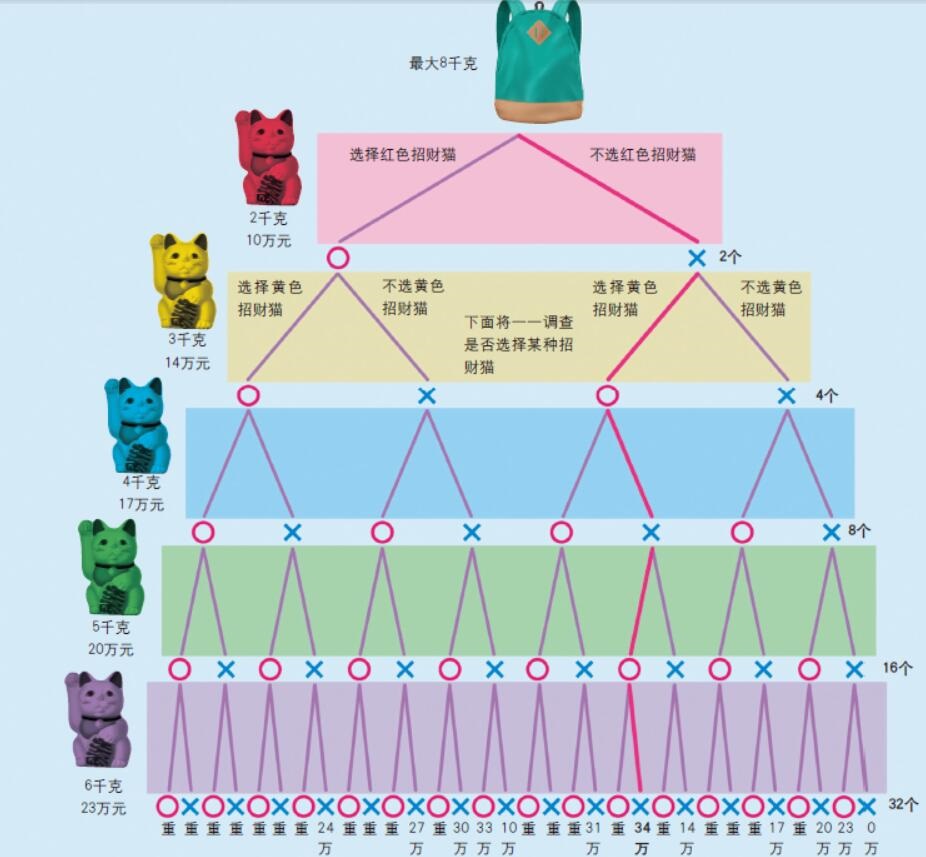
图3. 每增加一个物品，选择项增加一倍

通过将背囊问题中招财猫的所有可能组合一一列举，推导出答案。○标志表示选择该招财猫，×标志表示不选择该招财猫。在背囊问题中，每增加一只招财猫，可能的组合种类会变为原来的两倍。

最下层的“重”表示超重。另外各数值表示价格合计额。那么五种招财猫的答案为：应选择黄色招财猫（3千克）和绿色招财猫（5千克）。价值总计34万元。

（本文发表于《科学世界》2011年第8期）