互动科普

所谓“三色”问题是这样的：几个小圆圈相互之间用直线相连，在圆圈里涂上颜色。规则是每条直线所连接的圆圈必须是不同颜色的。另外直线可以任意连接两个圆，但是直线不能相互交叉。这时，可以用红黄蓝3种颜色将所有的圆圈都上色吗？

如下图的例子，实际尝试一下涂色的话，我们会凭直觉明白，用3种颜色是可以涂开的。但是如果像刚才“背囊问题”那样，为了找到答案将可能的颜色组合项一一老老实实地尝试一遍的话，会发现确实是可以涂开的。在所有的颜色组合中，当然也有的组合是违反规则的，但是用3种颜色确实可以符合要求。

图1. 只有三色可以做到吗？

4个白色圆点由直线相连。将4个白色圆点任意涂成红黄蓝三色。但是直线两端的圆点必须是异色的。只用3种颜色，可以做到吗？

如果圆圈数为30的话，涂色方案将超过200万亿个

首先考虑只有一个圆圈的情况。因为只是给一个圆圈涂色，共有涂黄、涂蓝、涂红3种方法。接下来考虑两个圆圈的情况。其中一个圆圈的颜色有红、黄、蓝3种选择，另一个圆圈也同样有3种选择，所以所要考虑的组合有3×3=9种。当有3个圆圈时，同样的就是3×3×3=27种，有4个圆圈时就是3×3×3×3=81种组合了。

在“背囊问题”中，每增加一个物品，组合数会变为原来的2倍。而在“3色问题”中，每增加一个圆圈，组合数将变为原来的3倍。如果圆圈数为n的话，颜色组合数为3n。

与背囊问题相同，圆圈数目只要稍微增加一点，就意味着求解所需的计算量将戏剧化地增长（可以说比背囊问题增加得更多）。如下图所示，圆圈数为10，组合数为59049个。如果圆圈数为20的话，组合数为3486784401个，如果圆圈数为30的话，组合数恐怕要有200万亿个。计算量将“飙升”到恐怖级别。

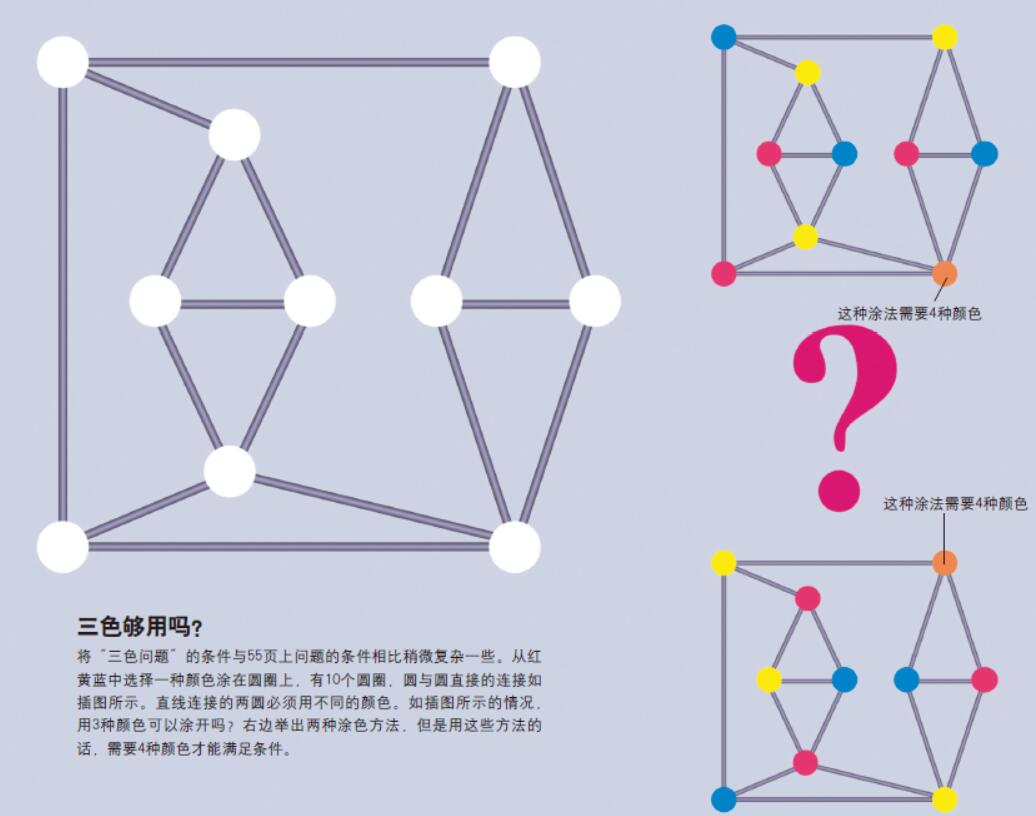
图2. 三色够用吗？

“三色问题”的条件与之前相比稍微复杂一些。从红黄蓝中选择一种颜色涂在圆圈上，有10个圆圈，圆与圆直接的连接如插图所示。直线连接的两圆必须用不同的颜色。如插图所示的情况，用3种颜色可以涂开吗？右边举出两种涂色方法，但是用这些方法的话，需要4种颜色才能满足条件。

此外，实际上使用4种颜色而不是3色的话，无论圆圈数目是多少，圆圈之间的连接多么复杂，也都一定可以涂开。这被称为“四色定理”。用4色是否可以涂开，在1976年得到证明以前，是让数学家们挑战百余年的难题。

三色问题是在用线连接的圆圈中涂色，而三色问题同样也可以用于给地图涂色上。给地图涂色时，其规则为：相邻领域。不管是什么地图，用4种颜色肯定都可以涂开（不考虑岛屿等不相连的领域）。

图3. 日本本州岛可以用三种颜色进行彩色化吗？

如果只用用3种颜色，是否可以将日本本州各都府县区分开呢？看一下日本本州地区地图，你就会发现这个问题很容易作答。比如我们关注岐阜县，作为内陆城市的岐阜县，与爱知县，三重县，滋贺县，福井县，石川县，富山县，长野县奇数个区域接壤。首先岐阜县的颜色要和周边区域的颜色区别开来。假如岐阜县用红色的话，周边的县从爱知县开始，按照蓝，黄，蓝，黄的顺序分别涂色。最后长野县为蓝色。但是如果长野县是蓝色的话，与接壤的爱知县为同一颜色，违反了规则。结果，其中某个县就需要用第4种颜色来涂。本州的都府县用3种颜色无法涂开。另外，即使没有这样内陆区域被奇数个区域完全包围的情况，也是需要4种颜色，三色问题不是能够简单解开的。

（本文发表于《科学世界》2011年第8期）