互动科普

“巡回销售员问题”也是一个具有代表性的“似易而难”的问题。它要解决的是，一个销售员以自己的公司作为出发点，拜访几家客户后，最后回到自己的公司，要选择哪条路线最节约时间。

在下面的例子中，因为客户只有3家，所以我们凭借直觉就可以得到答案。但是，巡回销售员问题和背囊问题、三色问题一样，随着问题“规模”的扩大，需要的计算量会相应飙升。

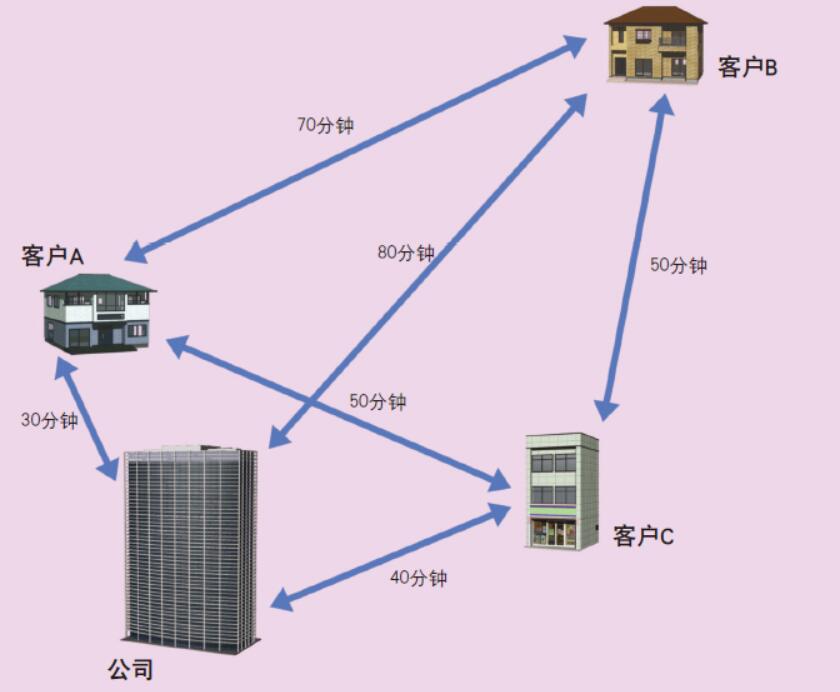
图1. 巡回销售员问题

某销售员以公司为起点，去拜访3家客户。上图表示了从公司到各客户的时间，以及各客户之间所需要的时间。如果从公司出发，每家客户都拜访，最后仍然回到公司的话，哪条路线最节约时间呢？

首先考虑只有3个客户的情况。这时，作为第一个目标的客户候补当然有3个。结束第一家的访问后，选择第二家拜访客户时，候补减少了1个，变为2个。这样选择第三个拜访客户时，候补就只剩下1个了。最后，从第三个客户处返回公司。这样的话，拜访3个客户的路线共有3×2×1=6种。但是，其中也包含着同样路线的相反路程，所以为了找到最省时路线，只需要调查3种路线就可以了。

如果有4家客户的情况，候选路线为4×3×2×1种，然后再除以2，最后为12种。像下图所示，有5家客户时，候选路线数目为5×4×3×2×1÷2=60种。

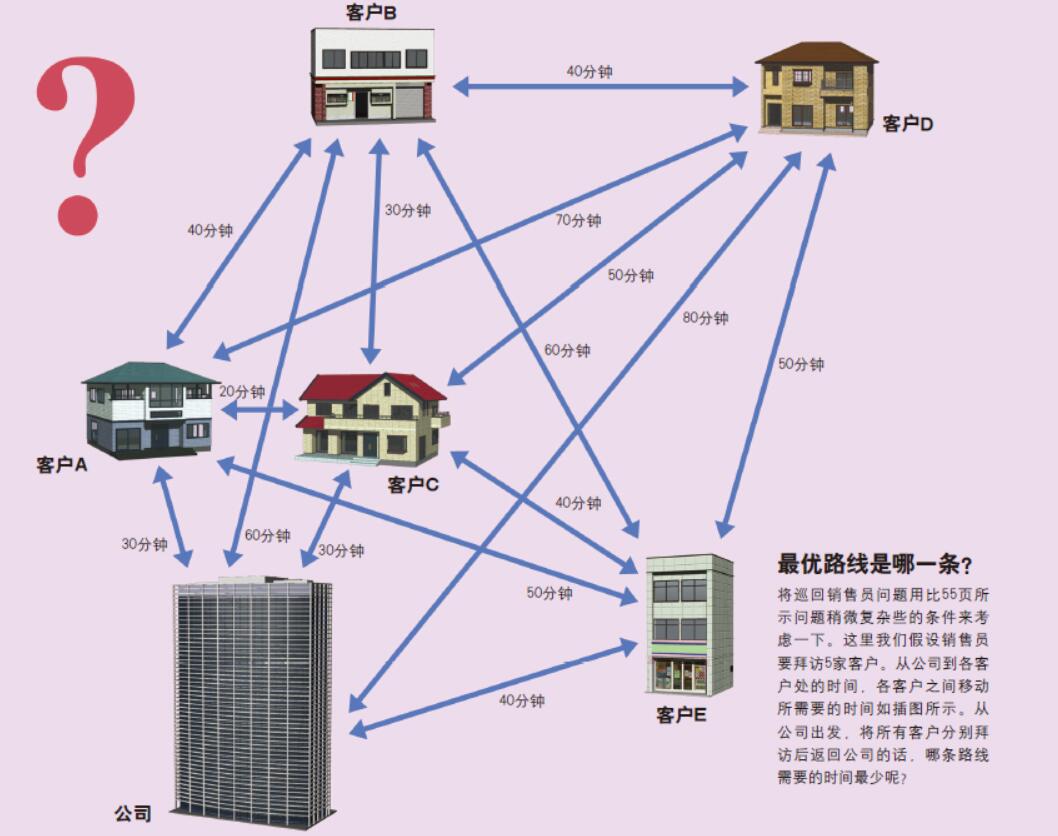
图2. 5家客户的巡回销售员问题

超过“n次方”发展为“阶乘”

在巡回销售员问题中，假设客户数为n，那么候补路线数为{n×(n-1)×(n-2)×⋯⋯×2×1÷2}种。其中{n×(n-1)×(n-2)×⋯⋯×2×1}的部分，可以用符号“n!”来表示，称为“n的阶乘”。

这个“阶乘”比背囊问题、三色问题中提到的2n，3n这样的“指数函数”更复杂，会引发计算量的“大爆发”。例如，当n为10时，10！为362.88万。且不说销售员，就是邮递员投递信件,拜访10家住户也是经常发生的。这时，为了选择最有效率的路线，要从362.88万的一半，也就是181.44万种候选路线中选出1种。如果集资方有20家的话，20的阶乘，大概为243京。1京等于1万亿的1万倍。

那么如果一个邮递员要给47家住户投递信件的话又会怎样呢？47的阶乘，大概为10的59次方,也就是1000万亿的1000万亿倍的1000万亿倍的100万亿倍，这已经是不可想象的数字了。

通过这样的推算，读者大概能感觉到计算量“爆发”的猛烈程度了吧。

（本文发表于《科学世界》2011年第8期）