互动科普

让我们再考虑另外一个问题:将下图中显示的100个随意排列的数字，按照从大到小的顺序排列好。一看到有100个数字，你会不会觉得这是个很费功夫的题目。如果我们还是“老老实实”地去解这个题目的话，就需要将某一数字和其他数字的比较的所有组合一一列出。

为了让题目简单一些，我们暂定有8个数字。将这8个数字，分别用符号a，b，c，d，e，f，g，h来表示。对于数字a来说，它需要同其他7个数字比较（因为a没有必要和自己比较），也就是说要比较7次。而这样的比较，从a进行到h，一共进行比较的次数为8×7=56种。但在这种计算方式中，将a和b、b和a看做不同的组合分别进行计数，所以需要56÷2。最后，进行比较的组合有28种。将所有组合进行比较，最后按每次比较的结果进行排序，就可以得出最终的结果。

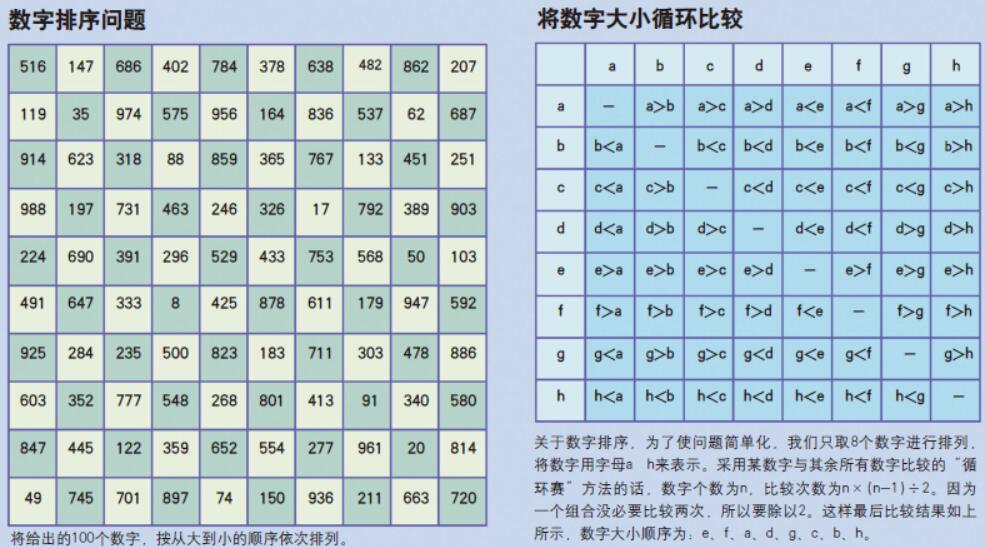
图1. 数字排序问题

计算量以“指数函数式”增长

当需要排序的数字有n个时，比较的次数会变为{n×(n-1)÷2}。这个式子可变形为：{(n²-n)÷2}。仔细观察这个公式，我们会发现，对比较次数（也就是为求解所需计算量）影响最大的是n²部分。

与此同时，在背囊问题或三色问题中，2ⁿ或3ⁿ部分决定着计算量的大小。n²也好，2ⁿ或3ⁿ也好，随着n的增加，其数值都将各自增大。不过，它们的数值增加速度有着本质上的差异。与n²相比，随着n的增加，2ⁿ或3ⁿ 的值的增加速度要快很多。

在由n²决定计算量的问题中，虽然随着n的增加计算量也会增加，但是如果使用高性能的计算机的话，这种问题在现实的时间中多数还是可以解决的。这种问题，被称为“多项式时间内可解”。也就是说“数字排序问题”是“可解”题。

另一方面，由2ⁿ或3ⁿ来决定计算量的问题，n只要稍微增大一点，计算量就会“爆发”。此外，在巡回销售员中，由n!来决定计算量，在这种情况下，计算量的“爆发”速度就更快了。这类问题被称为“需要指数系时间的问题”。需要指数系时间的问题，在现实时间中大多无法完成计算。在本文中，这样的问题被称为“无解题”。

例如巡回销售员问题中，如果是邮局的投递员需要给47家住户投递信件，大概有10⁵⁹种候选路线。如果假定计算机每秒可计算1000万亿种路线，那么该计算机将所有路线一一计算的话，用于计算的时间将超过10³⁶年（1000万亿年的1000万亿倍的100万亿倍）。即使是宇宙从诞生到现在所经过的时间也不过10¹⁰年。计算所需的10³⁶年是很不现实的数字。

图2. 多项式的增加与指数函数式的增加

上图是关于n²、2ⁿ、n!这3个函数，随着n的增大，各自数值增加速度的比较。n²属于“多项式”类型，其数值的增加比较缓和。但是“指数函数”类型的2 ⁿ和n!，增加速度就非常迅猛了。

用“计算程序算法”可以减少计算量

但是，难道没有更好的方法来解题吗？人们想了很多方法，比如在数字排序问题中，如果采用“淘汰赛方式”的话，可以大大减少比较次数。

在运动会中，我们经常会用到淘汰赛方式。像刚才那样为了比较8个数字的大小，首先让a和b、c和d、e和f、g和h进行初赛，各组合中的胜方再进行第2次赛，然后第2次赛中的胜方再进行第3次赛（本题中这就是决赛了）。最后胜利的一方是最大数。决定最大数需要的比赛次数（也就是比较次数）为7次。

第二大数字必定隐藏在直接败给第一大数字的那些数字中（3个侯选者），这些数字再进行淘汰赛，最后胜利的为第二大数字（决定第二名时需要比较2次）。同样，第三大数字必定隐藏在直接败给第一大数字或者直接败给第二大数字的那些数字当中。它们之间再进行淘汰赛，可以定出第三大数字。如此来决定顺序的话，如果a〜h之间的大小关系图1所示的话，共需16次比较，可以确定直到第8位数字的排列顺序。

这样我们可以看出，“老老实实”一一比较的方式进行排序的话，需要比较28次，采用淘汰赛的方式的话，计算量会减少。我们将类似“一一排查”或者“淘汰赛”的计算方法称为“计算程序算法”。如果在“计算程序算法”上多加考虑的话，有可能会减少计算量。

如果有合适的思路，背囊问题、三色问题或巡回销售员问题中的计算量“爆发”也有被抑制的可能。实际上，很多研究者在长年钻研这些问题的算法，最终，在一定程度上成功地减少计算量。其中一些算法的思路是，放弃严密追求最合适答案，而是先得到一个近似的最佳答案。还有一些研究者致力于将进行计算的计算机性能大幅提高，对于“规模”较大的问题在某种程度上也可以应对了。

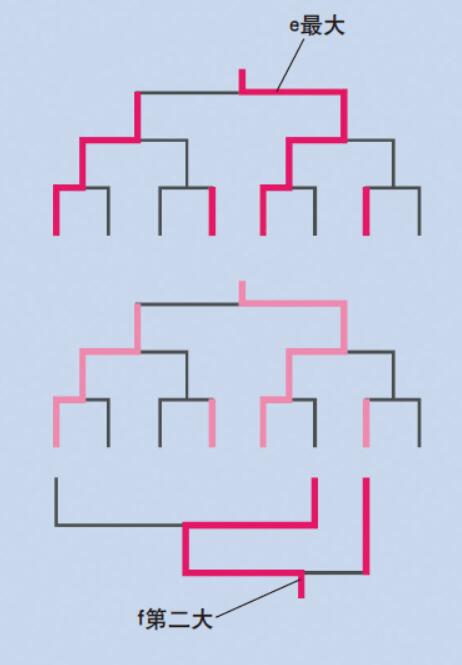
图3. 用“淘汰赛方式”计算次数减少

这里我们介绍的是用“淘汰赛方式”进行排序的方法。首先将数字一一组合，从初赛开始一直到决赛。这样通过7次比赛可以得出最大数字。将剩余的数字再进行淘汰赛，最后胜出的就是第二大数字。这样反复进行的话，就可以用比“循环赛”少的次数解开题目了。

但在另一方面，人们并没有找到从根本上减少计算量的算法。这里，“根本上”是指将“指数函数的”计算量控制在“多项式的”时间内。从这个角度来看，背囊问题、三色问题或者巡回销售员问题，依然是无解问题。

（本文发表于《科学世界》2011年第8期）