现在知道的最大素数已经有约1300万位,在它的后面还有更大的素数吗?有没有真正最大的素数,在它的后面就再没有素数了,它是最后一个素数吗?
其实,早在2300年前,欧几里得在他的《几何原本》中就已经给出了答案。在已经找到的素数的后面一定还有更大的素数。无论找到的素数有多大,都不会是最后一个素数,“素数有无穷多个”。
素数出现的频度逐渐减少
素数的个数虽然无穷,但是却无法预测它们在哪里出现。不过,尽管捉摸不定,也不是完全无法了解它们的性质。通过分析在越来越大的数中找到的那些素数,毕竟还是发现了它们出现的一个粗略规律。将自然数按照每100个数分段,记下每一段中出现的素数的个数。结果发现,随着数字的增大,素数出现的频度一直在减小。
那么,素数逐渐减少有什么规律吗?或者说,素数是以怎样的频度出现的呢?若能够知道素数出现的规律,就有可能找到求素数的公式。
素数出现个数体现的规律
最早研究这个问题的人是被人们视为天才的一位德国数学家和天文学家卡尔·弗雷德里希·高斯(1777〜1855)。高斯在15岁时就把自然数按照每1000个数分段,在各段中一个一个地寻找素数,并记下它们的个数。他在给别人的一封信中说,他每天都用15分钟的时间清点素数的个数,打算至少要检查够100万个数。在检查了数十万个数之后,高斯就发现了一个无需从头到尾一个一个地清点,可以用来计算出在某个自然数之前会出现的全部素数的个数。
不过,由高斯给出的这个公式计算得到的素数个数并不完全准确。虽然数字越大,得到的结果越准确,但是得到的毕竟不是正确的素数个数。素数的出现没有规律,利用这个简单的公式只能够知道素数的大致个数。由此也可以知道素数的性质十分奇特。
高斯当初并没有给出对这个公式的证明,后来才有其他的数学家用几种方法证明了这个公式成立。这个公式被称为“素数定理”。现在还找到了几个比高斯的这个公式更加准确的可以用来计算素数个数的公式。

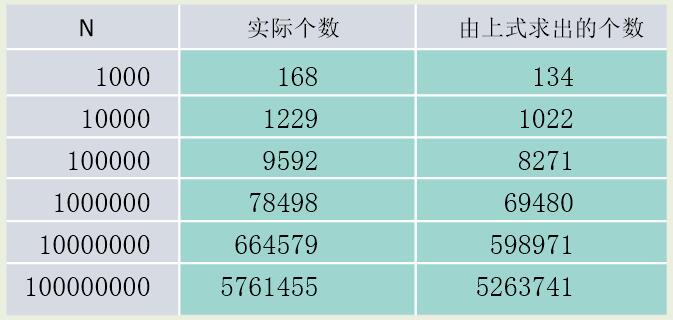
素数个数的求解公式(上),素数的实际个数和由公式求出的值(下)
由素数定理可以知道出现在某个数N以前的素数的大致个数。例如求6000以前的素数的大致个数,可以将6000代入式中的N,结果得到646.77。6000以前的素数的实际个数是783个。下表列出了出现在若干个大数以前的素数的实际个数和由素数定理求得的个数。现在已经有了更准确的估计素数个数的公式。
德国数学家伯恩哈德·黎曼(1826〜1866)就曾经证明过这个素数定理。他在1859年发表了一篇论文《论小于某个数的素数的个数》。在那篇论文中,他是先作出一个假设(关于素数的方程的所有有意义的解都在一条直线上),然后才对素数定理进行证明。黎曼的那个假设叫做“黎曼猜想”。只有黎曼猜想正确,素数定理才可以说得到了证明。然而,这个黎曼猜想是否正确直到现在仍然是一个谜。
关于素数还有许多没有解决的难题
围绕着素数,不仅存在着寻找求素数的公式和计算素数的个数的难题,还遗留有许多没有解决的其他难题。
其中有一个是关于“孪生素数”的难题。所谓孪生素数是指像11和13这样,彼此相差仅为2的一对素数。素数出现的频度随着自然数的增大而减小,它们的分布会变得越来越稀疏。但是,即使在非常大的自然数中仍然会偶尔出现一对孪生素数。那么,孪生素数是否也有无穷多对呢?
截至目前(2010年9月),已知的孪生素数有10.0355万位,已经非常大了。然而,我们仍然无法知道在它们的后面是否还会不断地出现更大的孪生素数。
另一个尚未解决的难题是一个猜想:“一切大于4的偶数全都可以表示为两个素数之和。”这个猜想是德国数学家克里斯蒂安·哥德巴赫(1690〜1764)提出来的,叫做“哥德巴赫猜想”。
对于小的偶数,这不难用计算验证(见下表)。例如4=2+2,6=3+3,8=5+3,10=7+3,12=5+7⋯⋯它们的确全都可以表示为两个素数之和。那么,其后的任何偶数真的毫无例外地也全都可以表示为两个素数之和吗?现在,利用计算机已经对直到12亿的10亿倍的所有偶数进行过验算,证实哥德巴赫猜想成立。不过,那个偶数之后还有无穷多个偶数,哥德巴赫猜想是否仍然成立并没有得到证明。
在对素数研究的发展做出过巨大贡献的数学家中,不能不提到欧拉(1707〜1783)。欧拉当时正在研究一个问题:“一切自然数的2次方的倒数的无穷项求和应该等于什么数值?”这里提到的某个数的倒数,比如说2的倒数为1/2,10的倒数为1/10,是指以该数为分母和1为分子的一个数。欧拉通过研究得到一个重要发现,即这个无穷项求和可以用一个包含了一切素数的无穷个因子的乘积来表示。
欧拉的研究进一步发展这个关系式,还得到了一个叫做“ζ函数”的表达式(“ζ”读作“泽塔”)。这个ζ函数是将欧拉先前得到公式中的所有含有2次方的部分的乘幂2改换成其他整数、负数甚至虚数等各种各样的数而得到的一个新的公式。

自然数与素数的关系
上图是欧拉发现的一个将自然数和素数联系起来的关系式。公式中的棕色数字是素数。将这个公式中的平方部分的乘幂2改换成3,4,-2等其他各种不同的数,便成为ζ函数(下图)。在这个公式中为S代入不同的值进行计算会得到什么结果,这就是“黎曼猜想”的内容。黎曼猜想是对ζ函数性质的一个猜想。
其实,在前面提到的那个可以说是最大的数学难题的“黎曼猜想”,就是若要求这个黎曼函数的计算结果为0,黎曼对其中的乘幂S应该取什么值的一种推测。换句话说,黎曼猜想是一个了解黎曼函数具有什么性质的难题。
黎曼提出他的这个猜想已经过去了150年,至今仍然没有解决。美国克雷数学研究所在2000年选定七个数学“千年大奖难题”悬赏征求答案,黎曼猜想就是其中之一,完成证明者将获得100万美元奖金。如今,许多数学家都在绞尽脑汁希望攻克这个难题。
(本文发表于《科学世界》2011年2期)
请 登录 发表评论