互动科普

这里介绍的是一个奇怪的“证明”，利用三条边长均为1的一个正三角形居然可以推导出“2＝1”。

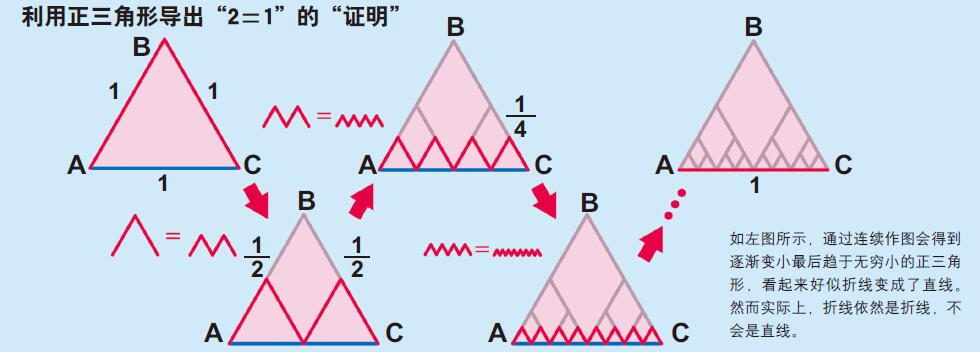
设有一个边长为1的正三角形ABC。这个三角形的AB边和BC边的长度均为1，二者之和等于2。我们从AB边和BC边各自的中点向AC边的中点引直线，结果形成两个边长为1/2的正三角形。考虑这两个新的正三角形的上侧边所形成的从A到C的那条折线，它由4条长度为1/2的直线连接而成，不用说，其总长度等于原来那个大三角形的AB边和BC边二者长度之和，即等于2。我们还可以利用这两个新三角形进行同样的作图，再得到四个边长均为1/4的正三角形。这四个三角形的上侧边所形成从A到C的那条新折线的长度仍然等于2。如此继续重复作图，得到的正三角形越来越多和越来越小，但是从A到C的折线的长度依然等于2。

不过，如此继续无穷多次地作图，从A到C的折线最后将变为直线AC（见右图）。A到C的折线的长度为2，而直线AC的长度为1，结论居然是“2＝1”。怎么会得到这样一个似是而非的结果呢?

原来这是一个疑似佯谬。在上面的推理中犯了一个逻辑错误，误以为“继续无穷多次作图，折线就会变为等同于直线AC”。无穷多个无穷小的三角形排列在一起，看起来好像等同于直线。然而，折线终归是折线，它绝不可能是直线。

（本文发表于《科学世界》2011年第3期）