互动科普

德国数学家戴维·希尔伯特（1862〜1943）曾经考虑过一个十分有趣的由假想的一家拥有无穷多套客房的“无限饭店”引出的问题。

某一天，一家有无穷多套客房的饭店已经住满了房客。这时，又来了一位客人，无处可去，要求这家无限饭店无论如何也要为他提供一套客房。饭店经理想了一个办法，终于安顿了这位客人。经理说服所有的房客全都从自己现在住的那套编号房间转移到另一套编号更大的房间里去。比如说，1号房的客人转移到2号房，2号房的客人转移到3号房⋯⋯原来住下的无穷多位客人全都如此转移，结果腾出1号房，让新来的客人住了进去。

又有一天，这家已经住满了无穷多个房客的无限饭店一下子又涌来了无穷多位新客人，要求入住。这家饭店是否有能力继续接纳如此多的新客人呢？

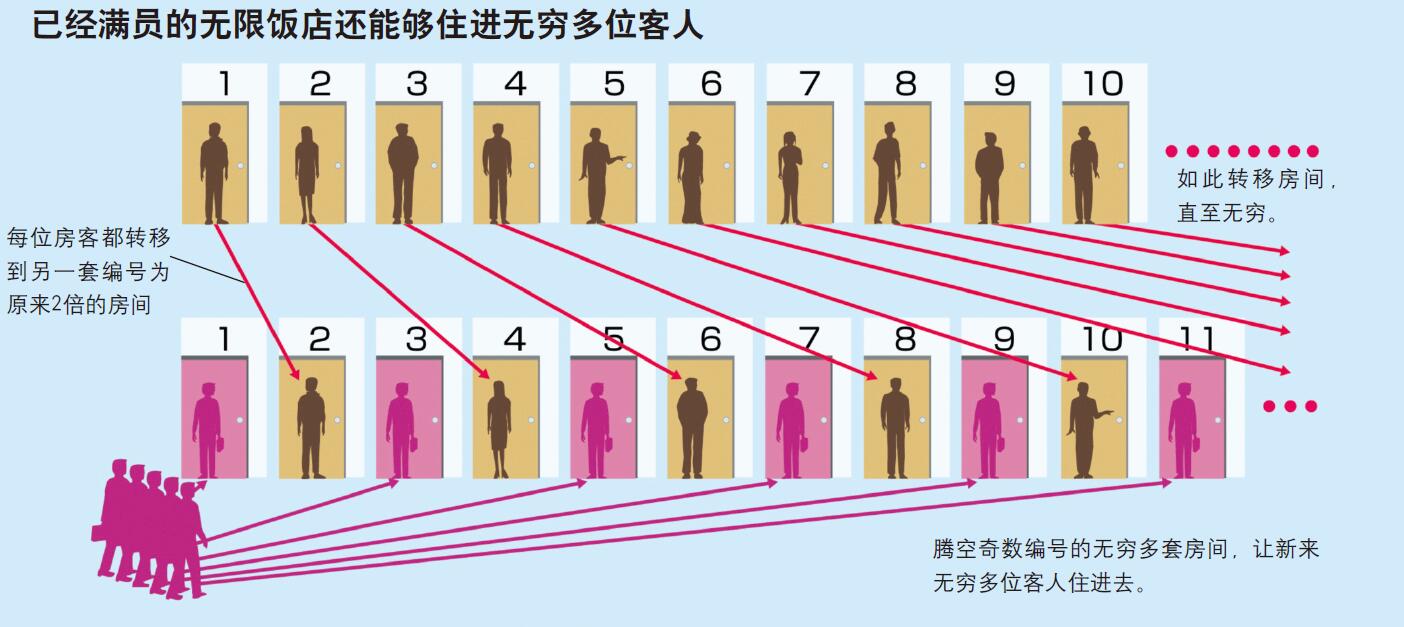
饭店经理自有办法。他说服已有的全部房客，每个人都从自己居住的房间转移到编号为原来房间编号2倍的房间。举例说，1号房客转移到2号房间，2号房客转移到4号房间，3号房客转移到6号房间⋯⋯如此等等。这样一来，原来的房客全都住进了编号为偶数的房间，空出来编号为奇数的无穷多套客房，饭店经理便可以有条不紊地将新来的无穷多位客人安排住进这些房间。

这个故事中，无限饭店经理的做法在数学上毫无问题，之所以成为疑似佯谬，是因为它同我们对无限的日常直觉相悖。我们从日常接触的有限世界得到的知识是，比如从1〜10的自然数（10个），其中偶数的个数（5个）只能比相应的自然数的个数少。然而在无限世界，全部偶数和全部自然数却能够一一对应，这两个集合的大小是相同的。也就是说，在无限世界，某个集合的部分集合同原来的全部集合具有相同的大小。这个性质，仅凭直觉，会觉得不可思议。       

（本文发表于《科学世界》2011年第3期）