“虚数的故事”一文(见《科学世界》2009年第1期)中,在对分数的介绍中,举了3个循环小数的例子,即:
1/7=0.142857142857142857…
1/17=0.05882352941176470588235294117647…
1/61=0.016393442622950819672131147540983606557377049180327868852459016393442622950819672131147540983606557377049180327868852459…
“虚数的故事”一文指出,表示这3个循环小数的轮盘两侧任何正对的两个数字相加,正好都等于9,如下图所示1/7的轮盘,相对两数1+8=9,4+5=9,2+7=9。1/17和1/61的情况与此相似。
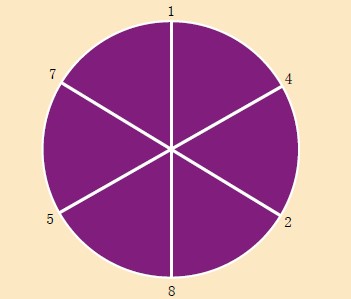
1/7轮盘
但是该文也指出,并非所有循环小数都具有这个特点。那么,什么样的循环小数具有这个特点,什么样的循环小数不具有这个特点呢?该文没有进一步介绍。本文就来回答这个问题,同时介绍循环小数的其他一些有趣特点。
循环小数的循环周期
循环小数中循环出现的数字叫做“循环节”。所谓循环小数的循环周期指循环节的位数,例如:
1/3=0.3333…,则其循环周期等于1;
1/7=0.142857142857…,则其循环周期等于6;
1/13=0.076923076923…,则其循环周期也等于6;如此等等。
显然,若1/n是一个循环小数,则其循环周期可能的最大值等于(n-1)。循环周期是循环小数的一个重要参数,循环小数的许多重要性质就是由循环周期决定的。循环小数的轮盘两侧任何正对的两个数字相加,是否正好都等于9,这个性质就同循环周期有关。
首先,我们注意到,循环小数的轮盘两侧任何正对的两个数字相加,正好都等于9,换一种说法,就是循环节的前一半数字和后一半数字相加,正好等于若干个9。例如,对于1/7来说,就是:
142+857=999
因此,循环小数的轮盘两侧任何正对的两个数字相加,正好都等于9这一性质成立的第一个条件就是循环周期为偶数。
但是,循环周期为偶数的循环小数,其轮盘两侧任何正对的两个数字相加,不一定正好都等于9。但凡循环周期为最大值(n-1)的,则其轮盘两侧任何正对的两个数字相加,一定正好都等于9。本文开头列举的3个循环小数1/7的循环周期是6,1/17的循环周期是16,1/61的循环周期是60,都符合(n-1)的条件,因此它们的轮盘两侧任何正对的两个数字相加,正好都等于9。
当然,循环周期为最大值(n-1)只是这一性质得到满足的充分条件,而非必要条件。例如1/13=0.076923076923…,其循环周期为6,只是n-1=12的一半,但其循环节的前一半076加后一半923之和也等于999。
从循环小数到循环数到卡泼里卡数
循环小数非常有趣。我们以1/7为例,在它上面分别乘以1、2、3、4、5、6,看有什么情况:
1/7×1=0.142857…
1/7×2=0.285714…
1/7×3=0.428571…
1/7×4=0.571428…
1/7×5=0.714285…
1/7×6=0.857142…
我们看到,1/7分别乘以2、3、4、5、6以后获得的数的组成同1/7完全一样,只是次序发生了变化。数学家把这样的数叫做“循环数”(cyclic number),142857是循环数之一。如果把0~9这10个数字均匀地安排在一个圆周上,那么,顺序连接循环数中的各个数字会形成一个很引人注目的对称图案,如下图所示。
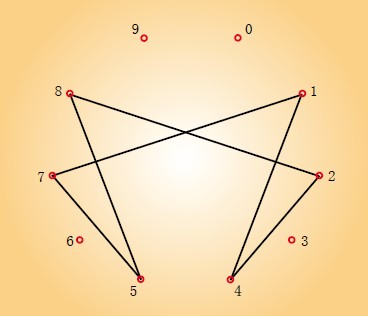
对称图案
把循环数142857乘以7以上的数字时,也会出现有趣的现象。例如:
142857×12=1714284
如果把乘积首位的1取下来加到末位的4上去,结果得到了循环数的另一形式714285,相当于142857×5。
一般而言,如果在142857上乘以任意正整数m,m=7×a+b,1≤b≤6,且0<a<10,那么经过以上处理,即把开头的一个数字挪到末尾去和最后一个数字相加;如果10≤a<100,则把开头的两个数字挪到末尾去和最后两个数字相加;余类推,其结果都相当于142857×b!当然了,如果m正好是7的倍数,那么142857×m再经过以上处理以后,会变成999999,也就是相当于142857×7。
循环数同9有着千丝万缕的关系。前面我们提到,把142857分成3位3位一组相加得999;类似的,把142857分成2位2位一组相加则得99,你看:
14+28+57=99
把142857分成1位1位相加则得9(答案超出2位时重复这个过程):
1+4+2+8+5+7=27, 2+7=9
把142857分成3位3位一组相加得999,分成2位2位一组相加得99,这一性质对142857的任意倍数(0除外)都成立,只要遵守分组从个位开始,答案超出3位或2位时重复这个过程这样2个规则。例如,对142857的361倍:
142857×361=51571377
51+571+377=999
51+57+13+77=198, 1+98=99
对142857取平方也产生有趣的结果:
1428572=20408122449
把结果分成前5位和后6位两个数相加:
20408+122449=142857
竟然又重新变成了原来的循环数!具有这种性质的数叫“卡泼里卡数”(Kaprekar Number)。
循环数的形成
我们知道,重复同一数字可以看成是比率为1/10的等比级数各项之和,例如:
666=600+60+6
循环小数也可以通过把某些等比级数以一定方式相加而获得。例如,可以通过把1、3、9…这个等比级数以如下方式相加而获得142857…:

也可以通过把7、35、175…这个等比级数由后往前相加而获得142857…:

最奇妙的恐怕是,可以通过把14、28、56…这个等比级数以如下方式相加而获得142857…:

循环周期不是最大值的循环小数的奇特性质
前面我们已经提到,循环小数1/13的循环周期为6,只是最大循环周期n-1的一半。这个循环小数有什么性质呢?我们也用2、3、4、…11、12去乘1/13,看看出现什么情况:
1/13×2=0.153846…
1/13×3=0.230769…
1/13×4=0.307692…
1/13×5=0.384615…
1/13×6=0.461538…
1/13×7=0.538461…
1/13×8=0.615384…
1/13×9=0.692307…
1/13×10=0.769230…
1/13×11=0.846153…
1/13×12=0.923076…
我们看到,这里出现了2个循环数,一个是076923,另一个是153846。前者出现在1/13乘1、3、4、9、10、12中,后者出现在1/13乘2、5、6、7、8、11中。如果把0~9这10个数字均匀地安排在一个圆周上,那么,这2个循环数中各数字的顺序连接同样会形成两个很引人注目的对称图案,下图所示076923的图案,153846的图案类似。
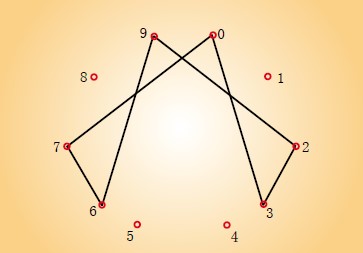
循环周期只是最大循环周期一半的循环小数1/13派生出2个循环数;循环周期更小的循环小数派生出的循环数就更多了。例如:
其循环周期为5,只是最大循环周期40的1/8。1/41乘以2、3、4、…39、40,其结果如下:
1/41=0.02439… 21/41=0.51219…
2/41=0.04878… 22/41=0.53658…
3/41=0.07317… 23/41=0.56097…
4/41=0.09756… 24/41=0.58536…
5/41=0.12195… 25/41=0.60975…
6/41=0.14634… 26/41=0.63414…
7/41=0.17073… 27/41=0.65853…
8/41=0.19512… 28/41=0.68292…
9/41=0.21951… 29/41=0.70731…
10/41=0.24390… 30/41=0.73170…
11/41=0.26829… 31/41=0.75609…
12/41=0.29268… 32/41=0.78048…
13/41=0.31707… 33/41=0.80487…
14/41=0.34146… 34/41=0.82926…
15/41=0.36585… 35/41=0.85365…
16/41=0.39024… 36/41=0.87804…
17/41=0.41463… 37/41=0.90243…
18/41=0.43902… 38/41=0.92682…
19/41=0.46341… 39/41=0.95121…
20/41=0.48780… 40/41=0.97560…
可以看出,这些结果可分成8组,每组中的5个数是由相同数字组成的循环数,因此共产生了8个循环数,即:
02439 04878 07317 09756
12195 14634 26829 36585
由于这些循环数的循环周期是奇数,因此不具有以上所说的许多特性。但是,每个循环数1位1位相加其和仍等于9;互补的数对(如1/41和40/41)所对应的2个循环数相加,其和一定仍等于99999。
(本文发表于《科学世界》2010年第4期)
请 登录 发表评论